Laboratorium Podstaw Metrologii
Semestr I
Ćwiczenie nr 6
Metody dyfrakcyjne w pomiarach średnicy drutów
SPRAWOZDANIE
Przebieg ćwiczenia
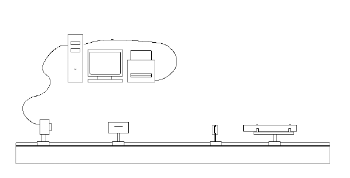
Opis stanowiska pomiarowego
Stanowisko pomiarowe składa się z:
1. źródła światła , w postaci lasera He-Ne;
2. elementu mierzonego (otworu lub drutu);
3. ekranu ;
4. detektora obrazu w postaci aparatu cyfrowego;
5. komputera PC wstępnie przetwarzającego dane uzyskane w wyniku pomiaru;
6. oraz drukującej je drukarki.
=
Przebieg ćwiczenia
Zarówno przy pomiarze średnicy otworu jak i średnicy drutu wykonywane czynności są
praktycznie identyczne stąd poniższy opis dotyczy obu przypadków:
Wykonanie 8 ekspozycji dyfrakcyjnego obrazu prążkowego dla obu elementów.
Wydruk zbiorów.
Pomiar odległości b ekranu od elementu mierzonego(różna dla otworu i drutu)
Pomiar długości podziałek na zdjęciach i porównanie ich z podziałką rzeczywistą w celu otrzymania współczynnika powiększenia.
Pomiar odległości pomiędzy symetrycznymi minimami na otrzymanych obrazkach.
Obliczanie średnicy drutu oraz otworu i odpowiadających im niepewności pomiarowych.
Zestawienie zmierzonych wartości wielkości wynikowych.
Pomiar średnicy drutu |
|||||||
Lp |
b (mm) |
p |
l |
a1 (mm) |
a2 (mm) |
a3 (mm) |
|
x |
295,625 |
0,85 |
|
8,81875 |
17,275 |
25,25 |
|
Sx |
1,157275 |
0,01069 |
|
0,257651 |
0,565054 |
0,801784 |
|
Średnica drutu s |
0,036062 |
0,036819 |
0,037785 |
||||
Niepewność pomiaru Δs. |
0,001648 |
0,001812 |
0,001823 |
||||
Średnica drutu s (wzór dokładny) |
0,036068 |
0,03684 |
0,037832 |
||||
Niepewność pomiaru Δs(dokładny |
0,0016481 |
0,001810448 |
0,0018206 |
||||
Pomiar średnicy otworu |
||||||
Lp |
b (mm) |
p |
l |
D1 (mm) |
D2 (mm) |
|
x |
399,375 |
0,96875 |
|
4,8125 |
8,625 |
|
Sx |
2,587746 |
0,025877 |
|
0,221601 |
0,353553 |
|
Średnica drutu d |
0,124097 |
0,126778 |
||||
Niepewność pomiaru Δd. |
0,009833 |
0,009405 |
||||
Średnica otworu s (wzór dokładny) |
0,124099 |
0,126786 |
||||
Niepewność pomiaru Δd.(dokładny) |
0,0098331 |
0,009404247 |
||||
b - odległość elementu od obrazu.
p - współczynnik powiększenia obrazu.
an, Dn - odległości symetrycznych minimów na obrazach prążkowych.
x - średnia wartość dla danej wielkości.
Sx - odchylenie standardowe wartości x (niepewność cząstkowa).
Co można powiedzieć o niepewnościach bezwzględnych?
Wartości Sx zależą od liczby pomiarów i maleją wraz z rosnącą ich liczbą. Można jednak pokazać, że wzrost liczby pomiarów od dziesięciu do kilkudziesięciu tylko w niewielkim stopniu wpływa na wartość niepewności. Istotną zmianę w wartościach niepewności otrzymamy dopiero po wykonaniu ponad stu pomiarów. W naszym doświadczeniu niemożliwe wydaje się przeprowadzenie aż tak dużej liczby pomiarów. Tak więc obliczona niepewność bezwzględna nie miała by sensu ponieważ nie daje wyczerpującej informacji o wartości wyniku pomiarowego.
3. W jakich przypadkach można stosować wzory przybliżone?
Wzory przybliżone można z powodzeniem stosować przy obliczaniu średnicy drutu i otworu dla pierwszych dwóch, trzech rzędów, gdyż wartości średnic elementów dla wzoru uproszczonego i dokładnego różnią się naprawdę niewiele. Nie mogliśmy sprawdzić jak dzieje się dla wyższych rzędów gdyż na zdjęciach dało się określić tylko maksymalnie rząd 2 dla otworu i 3 dla drutu.
4. Zestawienie wartości niepewności pomiarów cząstkowych
Dla drutu |
|||||||
Lp |
b (mm) |
p |
l |
a1 (mm) |
a2 (mm) |
a3 (mm) |
|
x |
295,625 |
0,85 |
|
8,81875 |
17,275 |
25,25 |
|
Sx |
1,157275 |
0,01069 |
|
0,257651 |
0,565054 |
0,801784 |
|
Dla wzoru uproszczonego |
|||||||
Średnica drutu s |
0,036062 |
0,036819 |
0,037785 |
||||
Niepewność pomiaru Δs. |
0,001648 |
0,001812 |
0,001823 |
||||
Δ an |
0,001054 |
0,001204 |
0,0012 |
||||
Δ b |
0,000141 |
0,000144 |
0,000148 |
||||
Δ p |
0,000454 |
0,000463 |
0,000475 |
||||
Dla wzoru dokładnego |
|||||||
Średnica drutu s (wzór dokładny) |
0,036068 |
0,03684 |
0,037832 |
||||
Niepewność pomiaru Δs(dokładny |
0,0016481 |
0,001810448 |
0,0018206 |
||||
Δ an |
0,0010534 |
0,001203604 |
0,0011983 |
||||
Δ b |
0,0001411 |
0,000144048 |
0,0001477 |
||||
Δ p |
0,0004535 |
0,000462795 |
0,0004746 |
||||
Dla otworu |
||||||
Lp |
b (mm) |
p |
l |
D1 (mm) |
D2 (mm) |
|
x |
399,375 |
0,96875 |
|
4,8125 |
8,625 |
|
Sx |
2,587746 |
0,025877 |
|
0,221601 |
0,353553 |
|
Dla wzoru uproszczonego |
||||||
Średnica drutu d |
0,124097 |
0,126778 |
||||
Niepewność pomiaru Δd. |
0,009833 |
0,009405 |
||||
Δ Dn |
0,005714 |
0,005197 |
||||
Δ b |
0,000804 |
0,000821 |
||||
Δ p |
0,003315 |
0,003387 |
||||
Dla wzoru dokładnego |
||||||
Średnica otworu d (wzór dokładny) |
0,124099 |
0,126786 |
||||
Niepewność pomiaru Δd.(dokładny) |
0,0098331 |
0,009404247 |
||||
Δ Dn |
0,0057142 |
0,005196527 |
||||
Δ b |
0,0008041 |
0,000821406 |
||||
Δ p |
0,0033148 |
0,003386314 |
||||
Dla pomiaru średnicy drutu największy wpływ na całkowitą niepewność wynikową ma niepewność cząstkowa związana z pomiarem odległości kolejnych minimów, zaś dla pomiaru średnicy otworu nie da się jednoznacznie określić która z niepewności cząstkowych ma największy wpływ ale można zauważyć że niepewność związana z pomiarem odległości otworu od ekranu zdecydowanie odstaje od pozostałych dwóch niepewności jest od nich blisko cztero pięciokrotnie mniejsza.
5. Wnioski:
Dla zmniejszenia niepewności pomiarowych należy z większą dokładnością dokonywać pomiaru odległości między minimami oraz pomiaru długości podziałki na zdjęciu w celu otrzymania dokładniejszego współczynnika powiększenia.
Wzory użyte do obliczenia niepewności pomiarowych
niepewność średnicy drutu w oparciu o wzór uproszczony:
Pomiar średnicy drutu |
||||||
Lp |
b (cm) |
p |
l |
a1 (mm) |
a2 (mm) |
a3 |
1 |
295 |
0,87 |
|
9,25 |
18,5 |
25,5 |
2 |
295 |
0,85 |
|
8,75 |
17,5 |
24 |
3 |
297,5 |
0,85 |
|
9 |
17 |
24,5 |
4 |
295 |
0,86 |
|
8,5 |
17,5 |
25 |
5 |
295 |
0,85 |
|
9 |
16,7 |
26 |
6 |
295 |
0,84 |
|
8,5 |
17 |
25,5 |
7 |
297,5 |
0,84 |
|
8,8 |
17 |
25 |
8 |
295 |
0,84 |
|
8,75 |
17 |
26,5 |
Pomiar średnicy otworu |
|||||
Lp |
b (mm) |
p |
l |
D1 (mm) |
D2 (mm) |
1 |
402,5 |
0,95 |
|
4,75 |
8,5 |
2 |
400 |
0,95 |
|
4,75 |
8,5 |
3 |
397,5 |
1 |
|
5 |
9 |
4 |
400 |
1 |
|
5 |
8,5 |
5 |
395 |
1 |
|
5 |
9 |
6 |
397,5 |
0,95 |
|
4,5 |
8 |
7 |
400 |
0,95 |
|
5 |
8,5 |
8 |
402,5 |
0,95 |
|
4,5 |
9 |
4
Wyszukiwarka
Podobne podstrony:
9471
9471
1 modul 7id 9471 Nieznany (2)
9471
9471
9471
więcej podobnych podstron