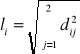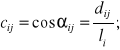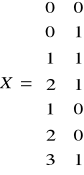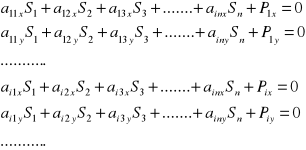
1. Cel ćwiczenia

Celem ćwiczenia jest zapoznanie się z zastosowaniem rachunku macierzowego do określania sił w prętach kratownicy statycznie wyznaczalnej.

2. Wstęp teoretyczny

Kratownicę statycznie wyznaczalną będziemy nazywali kratownicę, w której liczba niewiadomych sił w prętach oraz reakcji podporowych jest równa liczbie równań równowagi. Rozważania ograniczymy do kratownic płaskich, spełniające założenia technicznej teorii kratownic, tzn. odpowiednio podpartych ( statycznie zewnętrznie wyznaczalnych ), geometrycznie nie zmiennych zbudowanych z prętów przegubowych i obciążonych w węzłach. W takim przypadku siły w prętach tworzą w każdym z węzłów kratownicy zbieżny układ sił. Dla kratownicy posiadającej m węzłów oraz n prętów możemy napisać 2m równań równowagi odpowiadających rzutom sił na osie układu współrzędnych:

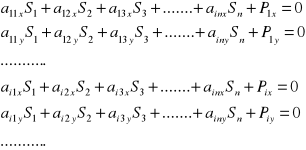
i = 1..,m, j = 1..,n

S - siła wewnętrzna w pręcie

a - współczynnik w równaniu równowagi dla węzła zrzutowanym odpowiednio na osie x i y układu współrzędnych stojące przy sile wewnętrznej

P - rzuty sił zewnętrznych na osie układu współrzędnych przyłożonych w węźle

Współczynniki a mogą być równe zero lub być różne od zera w zależności od tego , czy dany pręt występuje w rozpatrywanym węźle, czy też nie występuje . Układ równań równowagi można zapisać zatem w postaci macierzowej :

P = -A * S

gdzie: P - macierz kolumnowa składowych sił zewnętrznych przyłożonych w węzłach zawierająca niewiadome podporowe ,

A - macierz współczynników równań równowagi węzłów,

S - macierz kolumnowa sił wewnętrznych .

1. Budowa macierzy połączeń

Macierz połączeń zawiera konfiguracje kratownicy , tzn . zapisana jest w niej informacja o połączeniach prętów w poszczególnych węzłach . Obliczenia rozpoczynamy od ponumerowania w dowolnej kolejności węzłów i prętów kratownicy. Przyjmujemy że początkiem węzła jest węzeł o niższym numerze. Następnie budujemy macierz połączeń węzłów

K = [k_ij]; i = 1,2...m; j = 1,2...n.

gdzie : m - liczba węzłów ,

n - liczba prętów ,

i - numer węzła ,

j - numer pręta.

2. Budowa macierzy współrzędnych węzłów

Obieramy dowolny prostokątny układ współrzędnych . Macierz współrzędnych węzłów ma następującą postać:

X = [x_ij]; i = 1,2...n; j = 1,2.

3. Budowa macierzy cosinusów kierunkowych

W macierz tej zapisane są cosinusy kierunkowe poszczególnych prętów kratownicy , a co za tym idzie, poszczególnych sił wewnętrznych . Zbudowanie tej macierzy wymaga określenia składowych długości prętów w przyjętym układzie współrzędnych oraz wyznaczenia ich całkowitej długości. Na tej podstawie możemy dopiero określić cosinusy nachylenia poszczególnych prętów kratownicy do osi układu współrzędnych.

Macierz składowych długości prętów:

D = [d_ij]; i = 1,2...n; j = 1,2

obliczmy z równania

D = - K^T X

Długości prętów są równe

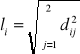
a ich cosinusy kierunkowe

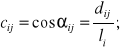
i = 1,2...n; j = 1,2.

Macierz cosinusów kierunkowych C ma następującą postać:

C = [c_ij]

4. Budowa macierzy sił zewnętrznych

Zakładamy że w węzłach kratownicy są przyłożone siły zewnętrzne, których składowe są elementami macierzy P.

Między macierzami sił zewnętrznych P i wewnętrznych S zachodzi związek wynikający z równowagi węzłów

P = - A*S

5. Budowa macierzy współczynników równań równowagi węzłów.

Macierz A powstaje z macierzy K przez podstawienie w miejscu elementów:

„1” - odpowiednich wierszy macierzy cosinusów kierunkowych z macierzy C, odpowiadających poszczególnym prętom kratownicy,

„-1”-jw.,ale ze znakiem przeciwnym,

„0” -dwuelementowego wektora zerowego .

Wyznaczenie sił wewnętrznych wymaga wyeliminowania z macierzy A wierszy, a z macierzy kolumnowej P elementów odpowiadającym warunkom podparcia. Po rozwiązaniu takiego uproszczonego układu równań wyznaczymy siły wewnętrzne w prętach kratownicy . Wartość dodatnia sił oznacza , że pręt jest rozciągany , a ujemna , że ściskany.

Znając wartość tych sił i korzystając z odrzuconych równań zawierających składowe reakcji możemy wyznaczyć reakcję w podporach .

PROTOKÓŁ POMIAROWY

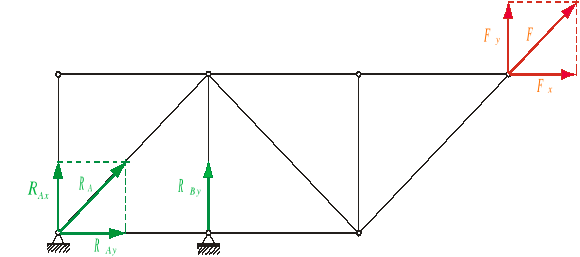
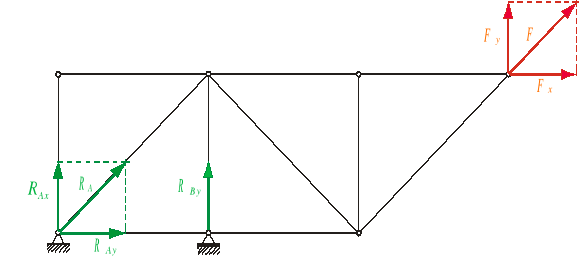
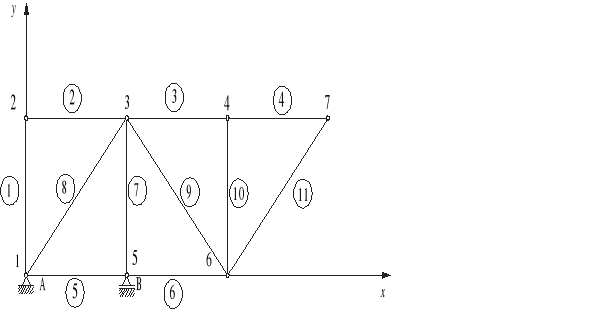
Kratownica przedstawiona na poniższym rys. , jest statycznie wyznaczalna (spełniony jest warunek p = 2w - 3), jest geometrycznie niezmienna, zbudowana z prętów przegubowych i obciążona w węzłach. Można w takim wypadku obliczyć siły działające w prętach oraz reakcje na podporach .

Dane :

- kratownica jest zbudowana na module

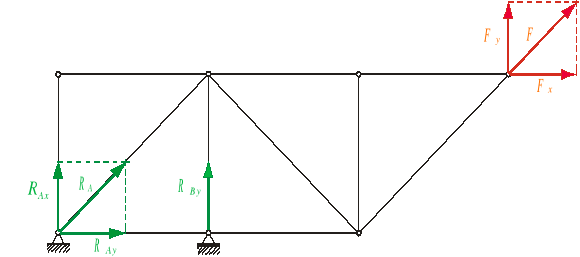
kwadratowym o boku 1m

- obciążenie F = 502,5 kN

(F_x = 50 kN , F_y = 500 kN )

Macierz połączeń zapisana jest dla kratownicy z odpowiednio ponumerowanymi prętami.

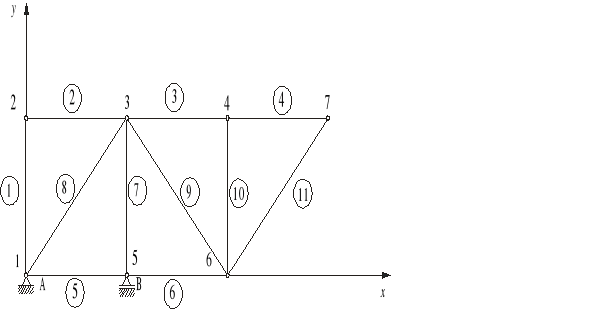
Dla tak ponumerowanej kratownicy można zbudować macierz

Następnie macierz współrzędnych węzłów

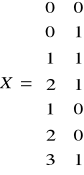
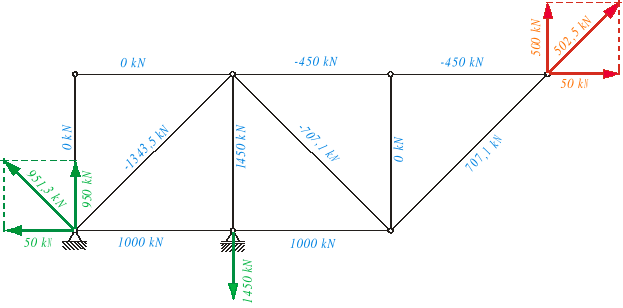
Po podstawieniu danych do programu komputerowego otrzyma się następujące wyniki :

• siły występujące w prętach :

S₁ = 0

S₂ = 0

S₃ = - 450 kN

S₄ = - 450 kN

S₅ = 1000 kN

S₆ = 1000 kN

S₇ = 1450 kN

S₈ = -1343,5 kN

S₉ = -707,1 kN

S₁₀ = 0 kN

S₁₁ = 707,1 kN

• podpora stała :

R_Ax = -50 kN

R_Ay = 950 kN

R_A = -951,3 kN

• podpora ruchoma :

R_B = -1450 kN

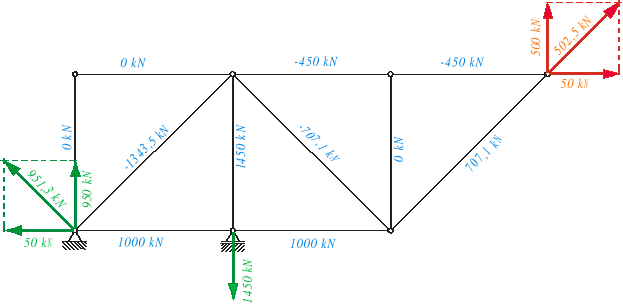
Wnioski:

Z analizy powyższych wyników widać ,że w obliczonej kratownicy zbędne są pręty 1, 2, 10 - w tych prętach wartość naprężeń jest równa zero. Dlatego kratownica ta mogłaby funkcjonować bez tych prętów .Obliczenia te były wykonane na komputerze , dlatego można wykluczyć błąd w rachunkach obliczeniowych.

1

2