Sprawozdanie nr 2

Skład grupy:

Adam Brzozowski,

Kamil Gniewek.

1. Programy do liczenia całek:

1. Metodą prostokątów

function[w]=prostokat(a,b,n,F)

m=length(n);

for k=1:m

n1=n(k);

h=(b-a)/n1;

x=a+h/2:h:b-h/2;

y=feval(F,x);

w(k)=0;

for i=1:n1

w(k)=w(k)+h.*y(i);

end

end

2. Metodą trapezów

function[w]=trapez(a,b,n,F)

m=length(n);

for k=1:m

n1=n(k);

h=(b-a)/n1;

x=a:h:b;

y=feval(F,x);

for j=1:n1

c=y(j+1);

d=y(j);

p(j)=((d+c)/2)*h;

end

w=0;

for j=1:n1

w=p(j)+w;

end

end

3. Metodą Simpsona

function[w]=simpson(a,b,n,F)

m=length(n);

for k=1:m

n1=n(k);

h=(b-a)/n1;

x=a:h/2:b;

y=feval(F,x);

w=0;

for k=1:2:2*n1

w=w+((y(k)+4*y(k+1)+y(k+2))*h)/6;

end

end

2. Całki:

1)
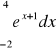
, wartość dokładna całki:

2)
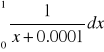
, wartość dokładna całki:

3)
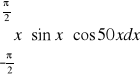
, wartość dokładna całki:

3.Wyniki

Rozbieżności pomiędzy wartością prawdziwą całki a obliczoną poprzez całkowanie metodą prostokątów, trapezów lub Simpsona porównujemy poprzez wykorzystanie błędu względnego:

,

oraz z wykorzystaniem błędu bezwzględnego:

1. Całkowanie metodą prostokątów

n=	5	8	13	16	25	32	49	64
całka 1	139.522	144.6316	146.7394	147.1814	147.6906	147.8286	147.9528	147.9911
	-0.06	-0.03	-0.01	-0.01	-0.01	-0.01	-0.01	-0.01
	-9.26	-4.15	-2.04	-1.60	-1.09	-0.95	-0.83	-0.79
całka 2	3.5722	4.0398	4.5224	4.7285	5.1703	5.4137	5.8315	6.0913
	-0.61	-56.14	-50.90	-48.66	-43.86	-41.22	-36.69	-33.86
	-5.64	-5.17	-4.69	-4.48	-4.04	-3.80	-3.38	-3.12
całka 3	1.9659	1.0973	-1.1061	-0.004	1.9987	0.0094	0.0001	0.0005
	-2416.1	-1349.1	1357.9	3.9	-2456.4	-12.5	-1.1	-1.6
	1.967	1.098	-1.105	-0.003	2.000	0.010	0.001	0.001

2. Całkowanie metodą trapezów

n=	5	8	13	16	25	32	49	64
całka 1	165.3985	154.9207	150.664	149.7761	148.7552	148.4788	148.2302	148.1537
	0.1117	0.0413	0.01	0.01	-0.0002	-0.0020	-0.0037	-0.0042
	16.62	6.14	1.88	1.00	-0.03	-0.30	-0.55	-0.63
całka 2	1002.2	627.6541	387.755	315.847	203.792	160.2877	106.5019	82.8507
	107.81	67.15	41.10	33.29	21.13	16.40	10.56	8.00
	992.99	618.44	378.54	306.64	194.58	151.08	97.29	73.64
całka 3	-2.0671	-1.1379	-1.121	-0.0203	-2.0026	-0.0121	-0.0021	-0.0014
	2538.5	1396.9	1376.2	23.9	2459.2	13.9	1.6	0.7
	-2.066	-1.137	-1.120	-0.019	-2.002	-0.011	-0.001	-0.001

3. Całkowanie metodą Simpsona

n=	5	8	13	16	25	32	49	64
całka 1	148.1475	148.0613	148.0476	148.0463	148.0454	148.0453	148.0453	148.0453
	-0.004	-0.005	-0.005	-0.005	-0.005	-0.005	-0.005	-0.005
	-0.63	-0.72	-0.73	-0.73	-0.74	-0.74	-0.74	-0.74
całka 2	336.4424	211.9112	132.2666	108.4346	71.3775	57.0384	39.3883	31.6777
	35.53	22.01	13.36	10.77	6.75	5.19	3.28	2.44
	327.23	202.70	123.06	99.22	62.17	47.83	30.18	22.47
całka 3	0.6216	0.3523	-1.1111	-0.0094	0.6649	0.0022	0.000642	-0.00076
	-764.65	-433.81	1364.00	10.55	-817.84	-3.70	-1.79	-0.07
	0.6224	0.3531	-1.1103	-0.0086	0.6657	0.0030	0.0015	0.0001

3.Wykresy

a) Całka 1




b) Całka 2




c) Całka 3




4.Wnioski

Dla całki pierwszej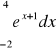
wartości obliczone poprzez metodę całkowania Simpsona leżą najbliżej wartości dokładnej dla małej liczby podprzedziałów lecz cechuje się bardzo wolnym wzrostem dokładności podczas ich zwiększania. Dla całki pierwszej metoda trapezów najszybciej osiąga wartości zbliżone do wartości dokładnej. Dla całki drugiej: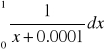
jak wynika z wykresu, najbardziej dokładną metodą całkowania jest metoda prostokątów, jest zbieżna do wartości dokładnej od najmniejszej liczby podprzedziałów. Metoda całkowania Simpsona i trapezów zbliżają się odpowiednio wolniej przy zwiększaniu liczby podprzedziałów. Ostatnią całkę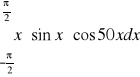
ze względu na największą trudność liczenia cechuje najmniejsza dokładność dla małej liczby podprzedziałów, porównując wykres i tabele z błędami względnymi możemy stwierdzić że metoda Simpsona jest najbardziej odpowiednia w przypadku liczenia tego typu funkcji gdyż dla małej liczby podprzedziałów całkowania posiada stosunkowo mniejsze błędy względne oraz jej wartości szybciej stają się zbieżne do wartości dokładnej w porównaniu do pozostałych metod.

---