![]()
Równanie różniczkowe zupełne
Równanie różniczkowe zupełne to równanie postaci:
![]()
gdzie lewa strona równania jest różniczką zupełną pewnej funkcji ![]()
Całka ogólna równania ma postać ![]()
gdzie funkcję F wyznaczono z układu:
![]()
Warunkiem koniecznym i dostatecznym istnienia funkcji F jest równość odpowiednich pochodnych cząstkowych:
![]()
Sposób rozwiązywania równań różniczkowych zupełnych wyjaśnimy na przykładach.
W rachunkach pomoże nam kalkulator ClassPad 300.
Przykład 1. Rozwiązać równanie:
![]()
Mamy kolejno:
![]()
a więc odpowiednie pochodne cząstkowe są równe.
Istnieje więc taka funkcja F, że
![]()
Wobec tego, przyjmując, że y jest stałe, dostajemy
![]()
więc w konsekwencji
![]()
Porównując odpowiednie pochodne cząstkowe stwierdzamy, że
![]()
![]()
![]()
czyli
![]()
a więc ostatecznie całka ogólna naszego równania ma postać:
![]()
![]()
Przykład 2. Rozwiązać równanie:
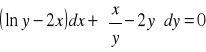
Mamy kolejno:
![]()
a więc odpowiednie pochodne cząstkowe są równe.
Istnieje więc taka funkcja F, że
![]()
Wobec tego, przyjmując, że y jest stałe, dostajemy
![]()
![]()
więc w konsekwencji
![]()
Porównując odpowiednie pochodne cząstkowe stwierdzamy, że
![]()
![]()
![]()
czyli
![]()
a więc ostatecznie całka ogólna naszego równania ma postać:
![]()
![]()
Przykład 3. Rozwiązać równanie:
![]()
przy warunku początkowym ![]()
Mamy kolejno:
![]()
a więc odpowiednie pochodne cząstkowe są równe.
Istnieje więc taka funkcja F, że
![]()
Wobec tego, przyjmując, że y jest stałe, dostajemy
![]()
![]()
więc w konsekwencji
![]()
Porównując odpowiednie pochodne cząstkowe stwierdzamy, że
![]()
![]()
![]()
czyli
![]()
a więc ostatecznie całka ogólna naszego równania ma postać:
![]()
Uwzględniając warunek początkowy otrzymujemy ![]()
, czyli całką (szczególną) naszego równania jest funkcja dana równaniem w postaci uwikłanej:
![]()