Probabilistyka, zwana również teorią prawdopodobieństwa, jest nauką formalną zajmującą się badaniem praw rządzących wynikami doświadczeń losowych lub zjawisk losowych. Do podstawowych narzędzi tej nauki należą zmienne losowe i pro-cesy stochastyczne. Za początek stworzenia współczesnej pro-babilistyki uważa się jej aksjomatyzację, której w 1933 dokonał Andriej Kołmogorow1.

Doświadczeniem (zjawiskiem) losowym nazywamy realizację określonego zespołu warunków, wraz z góry określonym zbiorem wyników Ω, zwanym zbiorem zdarzeń elementarnych. Po-szczególne wyniki ω∈Ω doświadczenia nazywamy zdarzeniami elementarnymi.

Zbiór Ω możliwych zdarzeń elementarnych Ω doświadczenia spełnia dwa postulaty:

P1) zawiera wszystkie zdarzenia, które mogą, lecz nie muszą wystąpić przy jednej realizacji doświadczenia,

P2) w jednym doświadczeniu może wystąpić tylko jedno zdarzenie z tego zbioru.

Zbiór Ω może być zbiorem skończonym, przeliczalnym albo nieprzeliczalnym.

Działem probabilistyki dostarczającym narzędzi do obliczania prawdop. zdarzeń, które są podzbiorami skończonego zbioru zdarzeń elementarnych jest kombinatoryka.

Zdarzeniem losowym (krótko: zdarzeniem) nazywamy każdy podzbiór A zbioru zdarzeń elementarnych Ω (A ⊆ Ω), który jest elementem przeliczalnie addytywnego ciała zdarzeń B (A∈B) i tylko taki zbiór.

Jeżeli Ω jest zbiorem skończonym, to każdy jego podzbiór może być zdarzeniem. W przypadku nieskończonego zbioru Ω nie jest to prawdą.

Działania na zdarzeniach

Sumą zdarzeń A, B ∈ B nazywamy zdarzenie A∪B, składające się ze zdarzeń elementarnych, które należą co najmniej do jednego ze zdarzeń A, B. Formalnie

A∪B = {ω∈Ω: ω∈A ∨ ω∈B}.

Iloczynem zdarzeń A, B ∈ B nazywamy zdarzenie A∩B, składające się z tych wszystkich zdarzeń elementarnych, które należą zarówno do zdarzenia A jak i do zdarzenia B. Formalnie

A∩B = {ω∈Ω: ω∈A ∧ ω∈B}.

Różnicą zdarzeń A, B ∈ B nazywamy zdarzenie A \ B, składające się z tych zdarzeń elementarnych, które należą do zdarzenia A i nie należą do zdarzenia B. Formalnie

A \ B = {ω∈Ω: ω∈A ∧ ¬ω∈B},

gdzie ¬ jest znakiem negacji.

Prawdopodobieństwo klasyczne

Jeżeli zbiór Ω jest skończony i wszystkie zdarzenia elementarne są jednakowo prawdop., to do obliczenie prawdop. dowolnego zdarzenia A⊆ Ω stosujemy tzw. prawdop. klasyczne sformułowane w roku 1812 przez Laplace'a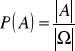
, symbol
oznacza liczebność zbioru A.

Prawdopodobieństwo geometryczne

Prawdop. geometrycznym nazywamy funkcję P: B → R określoną dla A∈B wzorem
, gdzie λ jest miarą Lebesque'a zdarzenia A będącą uogólnieniem pojęcia objętości, pola powierzchni, czy długości podzbiorów przestrzeni euklidesowej.

Przestrzeń probabilistyczna

Trójkę (Ω, B, P), gdzie

Ω jest zbiorem zdarzeń elementarnych,

B jest zbiorem zdarzeń,

P jest prawdopodobieństwem,

nazywamy przestrzenią probabilistyczną.

Przestrzeń probabilistyczna jest matematycznym modelem dowolnego doświadczenia, zjawiska lub obserwacji losowej.

Dla każdego doświadczenia (zjawiska) losowego istnieje przestrzeń probabilistyczna (Ω, B, P) opisująca jego losowość. Konstruując matematyczny model doświadczenia losowego należy wskazać te trzy elementy przestrzeni probabilistycznej.

Pomiar bezpośredni - doświadczenie polegające na przyporządkowaniu liczb przedmiotom (obiektom) lub wydarzeniom zgodnie z pewnym zbiorem reguł określających jednostki pomiaru, przyrządy pomiarowe, warunki pomiaru, itp. Wynikiem pomiaru są dwa rodzaje wielkości, te które mówią o liczebności zbioru obiektów, i te, które charakteryzują stopień nasilenia zjawiska wyrażony w pewnej skali pomiarowej.

Skala pomiarowa - zbiór W możliwych wyników pomiaru. Zwykle skala jest podzbiorem zbioru liczb rzeczywistych wyrażonych w pewnych jednostkach miary.

Wyróżniamy następujące skale pomiarowe: dychotomiczna, nominalna, porządkowa, przedziałowa i ilorazowa.

Dystrybuantą (ang. cumulative distribution function (CDF)) zm. l. X nazywamy funkcję rzeczywistą zmiennej rzeczywistej FX: R → R, określoną wzorem:

FX (x) = P(X ≤ x) = P{ω∈Ω: X(ω) ≤ x}.

Zmienna losowa typu ciągłego i jej rozkład

Zm. l. X o wartościach rzeczywistych nazywamy zm. l. typu ciągłego (continuous random variable), jeśli jej dystrybuanta F jest funkcją absolutnie ciągłą, tj. istnieje taka funkcja f ≥ 0, że dla każdego x∈R

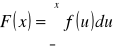
Obraz X(Ω) zm. l. typu ciągłego jest zbiorem nieprzeliczalnym, a prawd., że przyjmie szczególną wartość x wynosi zero, tj. P(X = x) = 0.

Zm. l. typu ciągłego zwykle jest modelem pomiaru wielkości fizycznych, np.: temperatury lub gęstości materiału.

Gęstością prawd. (krótko gęstością, ang. probability density function - PDF) zm. l. X ciągłej, nazywamy funkcję f(x) całkowalną w sensie Lebesque'a, która występuje pod znakiem całki określającej jej dystrybuantę.

Krzywą gęstości nazywamy wykres gęstości prawd. f(x). Jeżeli gęstość jest różna od zera tylko w przedziale (a, b), to mówimy, że rozkład jest skoncentrowany w tym przedziale.

Parametrem rozkładu zm. l. X nazywamy wielkość stałą od której zależy jej rozkład. Najczęściej stosowane rozkłady zależą od jednego lub dwóch parametrów. Zapis α∈J, gdzie J ⊆ R oznacza, że parametr α jest dowolną stałą ze zbioru J.

Jeśli dystrybuanta F(x) i gęstość (lub funkcja prawdop.) f(x) zm. l. X zależą od parametrów α i β, to stosowany jest zapis

F(x|α, β) i f (x|α, β),

z podaniem zakresów wartości parametrów. Zapis ten podkreśla, że funkcje CDF, PDF i PMF są rodzinami funkcji zależnymi od parametrów. Ustalenie wartości parametrów jest za-daniem statystyki matematycznej.

Funkcja kwantylowa i kwantyle

Niech F będzie dystrybuantą zm. l. X. Funkcją kwantylową (ICDF) nazywamy funkcję F^-1 określoną wzorem

F^-1(p) = inf {x∈R: F(x) ≥ p} dla p∈(0, 1)

Jeżeli F jest funkcją ciągłą i rosnącą, to F^-1 jest funkcją odwrotną w zwykłym sensie (inverse cumulative distribution function) i wówczas x = F^-1(p)

oznaczamy xp i nazywamy kwantylem rzędu p.

Kwantyle rzędów 0,25; 0,50 i 0,75 nazywamy kwartylami, przy czym kwantyl x0,5 nazywamy kwartylem środkowym lub medianą (ang. median), natomiast kwantyle x0,25 i x0,75 odpowiednio kwartylem dolnym i górnym.

Charakterystyki liczbowe zm. l.

Niech na (Ω, B, P) określone będą zm. l. X1,…, Xn o wartościach rzeczywistych. Charakterystykami liczbowymi zm. l. (lub ich rozkładów prawdop.) nazywamy liczby charakteryzujące zbiór wartości, jakie mogą one przyjmować, np. pod względem wartości najbardziej prawdop., rozrzutu wokół pewnej wartości, kształtu wykresu funkcji prawdop. lub krzywej gęstości, a w przypadku kilku zm. l. współzależności między nimi.

Charakterystyka liczbowa służy do syntetycznego opisu wartości zm. l. Za pomocą kilku liczb można uzyskać w prosty sposób dostatecznie dobre informacje o rozkładzie zm. l. lub zależnościach pomiędzy zm. l.

Charakterystyki położenia

Charakterystykę liczbową zm. l. X nazywamy charakterystyką położenia, jeśli dodanie do zm. l. dowolnej stałej zmienia wartość tej charakterystyki o tę stałą.

Do podstawowych charakterystyk położenia wartości zm. l. należą:

a) wartość oczekiwana (ang. mean),

b) wartość modalna (ang. mode)

c) kwartyle (ang. quartile).

Charakterystyki rozrzutu

Charakterystykę liczbową zm. l. nazywamy charakterystyką rozrzutu, jeśli dodanie do zm. l. dowolnej stałej nie zmienia wartości tej charakterystyki. Charakterystykami rozrzutu wartości zm. l. są:

a) wariancja (ang. variance),

b) odchylenie standardowe (ang. standard deviation),

c) odchylenie ćwiartkowe.

Względną charakterystyką rozrzutu jest współczynnik zmienności (ang. coefficient of variation).

Niech X będzie zm. l. określoną na (Ω, B, P) i ma wartość oczekiwaną m_X = E(X).

Wariancją (variance) zm. l. X nazywamy wartość oczekiwaną kwadratu scentrowanej zm. l., tj. liczbę określoną wzorem:

,

przy czym

a) dla zm. l. typu dyskretnego

,

b) dla zm. l. typu ciągłego

.

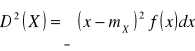
Wariancja zm. l. istnieje, gdy szereg (całka) występujący w definicji wariancji jest zbieżny. Mianem wariancji jest kwadrat miana badanej zm. l.

Odchyleniem standardowym (standard deviation) lub dyspersją zm. l. X nazywamy dodatni pierwiastek z wariancji, tj. liczbę
. Mianem dyspersji jest miano badanej zmiennej.

Momentem zwykłym r-tego rzędu (r jest liczbą naturalną) zm. l. X nazywamy charakterystykę liczbową określoną wzorem:

mr(X) = E(X^r)

Z istnienia momentów wyższych rzędów wynika istnienie momentów niższych rzędów. Wartość oczekiwana jest momentem zwykłym rzędu pierwszego.

Związek między wariancją a momentami zwykłymi

Jeżeli istnieje wariancja D2(X) zm. l. X, to
.

Momentem centralnym k-tego rzędu (k = 1, 2,…) (central moment of order k) zm. l. X nazywamy wartość oczekiwaną k-tej potęgi scentrowanej zm. l., tj.

Wariancja jest momentem centralnym rzędu drugiego.

Charakterystyki współzależności liniowej

Jeżeli rozważamy kilka zm. l. określonych na tej samej przestrzeni (Ω, B, P), to możemy badać je nie tylko z osobna, ale również współzależności między nimi.

W szczególności, charakterystykami określającymi współzależność liniową pomiędzy parą zm. l. są:

a) kowariancja,

b) współczynnik korelacji.

Niech na (Ω, B, P) określone będą zm. l. X1, X2,…, Xn o wartościach rzeczywistych.

Rozkładem Bernoulliego (Bernoulli distribution) (zwanym w polskiej literaturze rozkładem zerojedynkowym) nazywamy rozkład zm. l. X dla której X(Ω) = {0, 1}. Wartość 1 przyjmuje z prawdop. p, a 0 z prawdop. q = 1- p, czyli

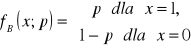
Rozkład ten oznaczamy B(p). Zapis X ~ B(p) oznacza, że zm. l. X ma rozkład Bernoulliego z parametrem p (p∈(0, 1)).

Rozkład równomierny i jego własności

Zm. l. X typu dyskretnego ma rozkład równomierny (discrete uniform distribution) na zbiorze X(Ω) = W, gdzie W = {x1, x2,…, xn}, co oznaczamy X·~ U(W), jeżeli każdą z wartości xk∈W przyjmuje z tym samym prawdop., tj.

fU(xk; W) = P(X = xk) = 1/n.

Rozkład równomierny jest modelem losowania liczby w totalizatorze sportowym, wyniku rzutu idealną kostką, losowania numeru produktu z ponumerowanej ich partii, itp.

Procesem Bernoulliego (Bernoulli process) nazywamy skończony lub nieskończony ciąg X1, X2,… identycznych i niezależnych zm. l. (i.i.d.) o rozkładzie Bernoulliego, tj. przyjmujących dwie wartości: 1 z prawdop. p zwanym sukcesem i 0 z prawdop. q = 1 - p zwanym porażką.

Z procesem Bernoulliego związane są rozkłady: Bernoulliego, dwumianowy i Pascala.

Rozkład dwumianowy i jego własności

Zm. l. X: Ω → {0, 1,…, n} ma rozkład dwumianowy (binomial distribution) z parametrami n i p (n∈N, p∈(0, 1)), co oznaczamy X ~ B(n, p), jeżeli jej funkcja prawdop. (PMF) fB wyraża się wzorem:

.

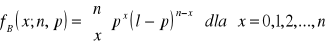
Zm. l. X o rozkładzie B(n, p) zlicza liczbę sukcesów (jedynek), w ciągu n niezależnych doświadczeń, których modelem jest proces Bernoulliego.

Rozkład jednostajny i jego własności

Zm. l. X: Ω → (a, b) ma rozkład jednostajny na przedziale [a, b] (uniform distribution), co oznaczamy X·~ U(a, b), je-żeli jej gęstość prawdop. (PDF) wyraża się wzorem

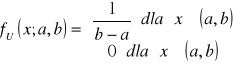
Rozkład normalny i jego własności

Zm. l. X typu ciągłego ma rozkład normalny z parametrami m i σ (m∈R, σ > 0), co oznaczamy X ~ N(m, σ), jeśli

.

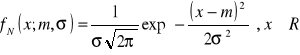
Gęstość rozkładu normalnego została zaproponowana przez Gaussa, jako model rozkładu częstości błędów pomiarowych. Na jego cześć krzywe gęstości rozkładów normalnych nazywamy krzywymi Gaussa.

Statystyka jako nauka dostarcza metod pozyskiwania, przetwarzania, zestawiania, analizy i prezentacji danych dotyczących wyników doświadczeń, obserwacji zjawisk losowych lub procesów masowych.

Wiele nauk zajmuje się obserwacją otaczającego nas świata lub też posługuje się eksperymentem dla potwierdzenia swoich teorii. Takie badanie przebiega zazwyczaj według schematu: zebranie dużej ilości danych, ich analiza i interpretacja. Badaczowi potrzebny jest wtedy zestaw metod, które umożliwią mu operowanie na dużych zbiorach danych.

Tworzeniem i rozwijaniem takich użytecznych narzędzi zajmuje się właśnie statystyka.

Statystyka opisowa - zespół metod, nie używających probabilistyki, służących do wydobycia dostępnej informacji zawartej w zbiorze danych uzyskanych podczas badania statystycznego, jako wyniku realizacji zjawiska lub doświadczenia losowego.

Celem stosowania metod statystyki opisowej jest podsumowanie zbioru danych i wyciągnięcie pewnych podstawowych wniosków dotyczących przedmiotu badań.

Przedmiotem badań statystyki opisowej są:

1. miary położenia: np. średnia, dominanta (moda), kwartyle,

2. miary dyspersji: np. wariancja, odchylenie standardowe,

3. miary asymetrii,

4. miary współzależności.

Statystyka matematyczna (SM) - sformalizowany ze-spół metod, używający probabilistyki, algebry liniowej i analizy matematycznej, służący do wnioskowania o własnościach wyodrębnionych populacji będących przedmiotem badań, na podstawie analizy danych częściowych, otrzymanych w eksperymencie lub z obserwacji pewnego zjawiska.

SM dostarcza teoretycznych podstaw do konstrukcji procedur statystycznych, w celu uzyskania wiarogodnej informacji o własnościach badanej populacji, na podstawie danych częściowych.

W SM dane częściowe stanowią próby losowe. Probabilistycznymi modelami tych prób są jedno- lub wielowymiarowe ciągi zm. l. Na przykład, (X1, Y1), (X2, Y2),..., (Xn, Yn) tworzy dwuwymiarową próbę losową (X, Y)n o liczebności n.

Statystyka jako funkcja - każda zm. l. U będąca funkcją próby losowej Xn = (X1, X2,..., Xn), tj. U = f(Xn). Statystyki służą do poznania mechanizmu generującego obserwacje.

Probabilistyka dostarcza twierdzeń dotyczących rozkładów statystyk. Są one podstawą metod statystycznych.

Badanie statystyczne to szereg czynności, związanych z pozyskiwaniem i przetwarzaniem danych, zmierzających do jak najlepszego poznania rozkładu wyróżnionych cech w populacji generalnej, których modelami są zm. losowe X, Y, Z.

BS może być pełne (obejmuje całą populację) lub częściowe (dotyczy pewnych elementów populacji - próby).

Czynniki, które przemawiają na korzyść badań częściowych:

- populacja może być nieskończona,

- badanie może być niszczące,

- wysokie koszty.

Populacja generalna i cecha statystyczna

Populacja generalna (zbiorowość statystyczna) to zbiór elementów zwanych jednostkami statystycznymi, podlegających BS. Jednostki populacji są do siebie podobne pod względem badanych cech, ale nie są identyczne.

Cechy statystyczne to te właściwości populacji generalnej, które są przedmiotem BS. Cecha statystyczna może być:

- mierzalna (ilościowe) - np. wzrost, waga, wiek

- niemierzalna (jakościowe) - np. kolor oczu, płeć

Zróżnicowanie wartości cechy statystycznej powoduje, że można mówić o jej rozkładzie w populacji. Modelami badanych cech statystycznych są zmienne losowe.

Wnioskowanie statystyczne

WS to sformalizowany zespół metod i procedur służących do uogólniania wyników badania próby na całą populację oraz szacowania błędów wynikających z takiego uogólnienia.

Wyróżniamy dwie grupy metod uogólniania wyników, definiujące jednocześnie dwa działy WS:

- Estymacja - szacowanie wartości nieznanych parametrów rozkładu badanych cech.

- Weryfikacja hipotez statystycznych - sprawdzanie poprawności przypuszczeń na temat rozkładu badanych cech w jednej lub kilku populacjach.

Próba a próba reprezentatywna

Próbą losową z populacji badanej ze względu na jedną cechę, której modelem jest zm. l. X, lub kilka cech, powiedzmy X i Y nazywamy:

w przypadku jednej cechy ciąg zm. l.

X1, X2,…, Xn oznaczany X lub Xn,

w przypadku dwóch cech ciąg par zm. l.

(X1, Y1), (X2, Y2),…, ( Xn, Yn) oznaczany (X, Y)

każda z określonym rozkładem prawdopodobieństwa.

Jeżeli badamy dwie populacje ze względu na wspólną cechę, to próbą losową są dwa ciągi: X1,1,…, X1,n i X2,1,…, X2,m.

Jeżeli zm. l.-owe w próbie są niezależne i o identycznym rozkładzie (i.i.d.) co badana cecha lub cechy, to mówimy, że jest to prosta próba losowa.

Próbą reprezentatywną nazywamy taką próbę, która zachowuje strukturę populacji ze względu na badane cechy. Sposobem pobierania prób zajmuje się dział statystyki zwany metody reprezentacyjne. Prosta próba losowa gwarantuje reprezentatywność.

Liczbę n jednostek wybranych do próby nazywamy liczebnością próby. Liczebność próby zależy m.in. od przyjętego błędu, zwanego poziomem ufności.

Jeżeli n ≤ 30 to próbę nazywamy małą próbą. W przeciwnym przypadku próbę nazywamy dużą próbą.

Operat losowania

Wykaz wszystkich elementów populacji nazywamy opera-tem losowania. Operat losowania pozwala wybierać elementy z populacji przez losowe generowanie numerów elementów, które znajdą się w próbie. Do generowania liczb losowych może być użyty komputer lub tablica liczb losowych.

Rozkład teoretyczny a rozkład empiryczny

Probabilistycznym modelem badanej cechy jest zm. l. X. Rozkład badanej cechy X w populacji nazywamy rozkładem teoretycznym. Rozkład ten zwykle nie jest znany i w badaniach statystycznych zwykle przyjmujemy, że jest to pewien rozkład spośród określonej rodziny rozkładów zależnej od nieznanych parametrów, np. X ~ N(m, σ), X ~ B(p).

Rozkład cechy lub kilku cech w próbie nazywamy rozkładem empirycznym. Rozkład ten poznajemy na podstawie BS opisującego wartości przyjmowane przez cechę lub cechy, zwykle przy pomocy dystrybuanty empirycznej, częstości ich występowania lub odpowiednich statystyk z próby. Niech (X1, X2,…, Xn) będzie jednocechową próbą prostą.

Dystrybuantą empiryczną nazywamy następująca funkcję:

dla każdego x ∈ R, Fn(x) = |{i: Xi ≤ x}|/n,

gdzie |A| oznacza liczebność zbioru A.

Twierdzenie o rozkładzie średniej arytmetycznej

Jeżeli cechę w populacji generalnej opisuje zm. l. X o rozkładzie N(m, σ), to średnia arytmetyczna z próby prostej X1, X2,…, Xn ma rozkład normalny N(m, σ/√n), tj. n X

Dowód tego tw. wynika z tw. o sumie niezależnych zm. l. o rozkładach normalnych.

CTG - centralne twierdzenie graniczne

Jeżeli X1, X2,…, Xn jest próbą prostą z populacji X o wartości oczekiwanej m i skończonym odchyleniu standardowym σ, to rozkład średniej z próby dąży do rozkładu normalnego o wartości oczekiwanej m i odchyleniu standardowym σ/√n, gdy liczebność próby wzrasta nieograniczenie, czyli dla dostatecznie dużych n

Siła CTG polega na tym, że rozkład populacji może być inny niż normalny, a nawet może być nieznany. Twierdzenie o standaryzowanym rozkładzie średniej arytmetycznej nazywa się tw. Lindeberga-Levy'ego.

Rozkład t-Studenta, jego własności i zastosowa-nie

Żeby zastosować CTG, powinniśmy znać σ w populacji. W praktyce, jeżeli σ nie jest znane, to korzystamy z jego estymatora Sn z próby. W tym przypadku standaryzowana statystyka:

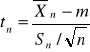
nie ma stand. rozkładu normalnego.

Rozkład statystyki tn jest bardziej płaski w środku i ma dłuższe „ogony” niż stand. rozkład normalny. Tw. Jeżeli rozkład cechy X w populacji jest normalny, to statystyka tn ma rozkład t-Studenta1 o n -1 stopniach swobody.

Zapis X~t(n) oznacza, że zm. l. X ma rozkład t-Studenta o n stopniach swobody.

Rozkład chi-kwadrat, jego własności i zastosowanie

Jeżeli X1, X2,…, Xn jest próbą prostą z populacji o rozkładzie normalnym, to statystyka

ma rozkład chi-kwadrat o n-1 stopniach swobody. Piszemy χn²~ χ²(n-1).

Estymacja punktowa (point estimation), to grupa metod statystycznych, służąca do punktowego oszacowania wartości nieznanego parametru rozkładu cechy w populacji.

Badany rozkład cechy X w populacji zależy od nieznanego parametru θ i parametr ten jest szacowany na podstawie prostej próby losowej Xn.

W szczególności, estymować można wartość oczekiwaną, wariancję i wskaźnik struktury badanych cech w populacji.

W przypadku badania populacji ze względu na dwie cechy estymować można współczynnik korelacji.

Estymatorem Un nieznanego parametru θ populacji generalnej nazywamy statystykę Un = h(Xn) służącą do jego oszacowania.

Oceną parametru - nazywamy każdą realizację un estymatora Un. Ocena parametru prawie zawsze różni się od rzeczywistej wartości parametru θ.

Miarą błędu estymacji jest różnica d = Un - θ.

Estymator wartości oczekiwanej

Średnia arytmetyczna jest estymatorem nieobciążonym i jednocześnie estymatorem największej wiarygodności wartości oczekiwanej zm. l., jeżeli przynajmniej:

- liczba obserwacji jest dostatecznie duża (zob. CTG),

- rozkład badanej cechy jest normalny.

Estymator wskaźnika struktury

Wskaźnikiem struktury nazywamy parametr p w populacji X ~ B(p), tj. prawdop. zaobserwowania wyróżnionej cechy.

Estymatorem wskaźnika p jest częstość z próby X1,…, Xn:

gdzie K = ΣXi jest liczbą elementów próby, które posiadają wyróżnioną cechę, a n jest liczebnością próby.

Estymacja przedziałowa, przedział ufności i po-ziom ufności

Estymacja przedziałowa to grupa metod statystycznych służących do oszacowania parametrów rozkładu cechy w populacji generalnej. W metodach estymacji przedziałowej oceną parametru nie jest konkretna wartość, ale pewien przedział, który z określonym prawdop. pokrywa nieznaną wartość parametru. Podstawowym pojęciem estymacji przedziałowej jest przedział ufności.

Niech cecha X ma rozkład w populacji z nieznanym parametrem θ. Z populacji wybieramy próbę losową (X1, X2, ..., Xn).

Przedziałem ufności nazywamy taki przedział (θ - θ1, θ + θ2), który spełnia warunek:

P(θ1 < θ < θ2) = 1 − α,

gdzie θ1 i θ2 są statystykami wyznaczonymi z próby losowej.

Pojęcie przedziału ufności zostało wprowadzone do statystyki przez Jerzego Spławę-Neymana. Jako kryterium wyboru najlepszych przedziałów ufności przyjmujemy te statystyki dla których otrzymamy najkrótsze przedziały.

Wielkość 1-α nazywamy poziomem ufności. Poziom ufności jest to prawdop., że wartość szacowanego parametru θ znajduje się w wyznaczonym przedziale ufności. Im większa wartość tego współczynnika, tym szerszy przedział ufności, a więc mniejsza dokładność estymacji parametru. Im mniejsza wartość 1  α, tym większa dokładność estymacji, ale jednocześnie tym większe prawdop. popełnienia błędu. Wybór odpowiedniego współczynnika jest więc kompromisem pomiędzy dokładnością estymacji a ryzykiem błędu. W praktyce przyjmujemy zazwyczaj wartości: 0,99; 0,95 lub 0,90.

Hipotezy statystyczne i ich podział

Weryfikację hipotez statystycznych ograniczamy tylko do klasycznej teorii J. Neymana i E. Pearsona, dotyczącej testów istotności (test of significance).

Hipoteza statystyczna (statistical hypothesis) to dowolne przypuszczenie dotyczące rozkładu cech w populacji, tj. postaci funkcyjnej lub wartości parametru rozkładu.

Przykłady hipotez statystycznych:

- czas dojazdu do pracy pracowników firmy A ma rozkład N(25, 5) (min),

- zawartości szkodliwych związków w spalinach samochodów z katalizatorem i bez katalizatora różnią się. Formułowanie hipotezy statystycznej rozpoczynamy od zebrania informacji na temat określonej cechy w badanej populacji i jej możliwego rozkładu. Dzięki temu możliwe jest zbudowanie zbioru hipotez dopuszczalnych, czyli zbioru rozkładów, które mogą charakteryzować badaną cechę (lub cechy) w populacji.

Formalnie, hipotezą statystyczną nazywamy każdy podzbiór zbioru hipotez dopuszczalnych.

Hipotezy statystyczne dzielimy na:

- hipotezy parametryczne (parametric hypothesis) - hipoteza dotyczy wartości parametru rozkładu

- hipotezy nieparametryczne - hipoteza dotyczy postaci funkcyjnej rozkładu

Według innego kryterium podział przebiega następująco:

- hipotezy proste (simple hypothesis) - hipoteza jednoznacznie określa rozkład danej populacji, czyli odpowiadający jej podzbiór zbioru Θ zawiera dokładnie jeden element (rozkład),

- hipotezy złożone (composite hypothesis) - hipoteza określa całą grupę rozkładów, zaś odpowiadający jej podzbiór zbioru Θ zawiera więcej niż jeden element.

Stwierdzenie: „wzrost badanej populacji jest określony rozkładem normalnym o parametrach m = 1,75m i σ = 10” jest hipotezą parametryczną, ponieważ określa wartość parametrów rozkładu oraz hipotezą prostą, bo jednoznacznie definiuje rozkład.

Stwierdzenie: „wzrost badanej populacji jest określony rozkładem normalnym” jest hipotezą nieparametryczną - nie dotyczy wartości parametrów rozkładu i złożoną - określa więcej niż jeden możliwy rozkład.

Weryfikacja hipotezy statystycznej

Weryfikacją hipotezy (hypothesis testing) nazywamy sprawdzanie sądów o populacji, sformułowanych bez zbadania jej całości. Przeprowadzamy ją na podstawie próby losowej X pobranej z populacji X, której hipoteza dotyczy. Przebieg procedury weryfikacyjnej przebiega w 5. krokach.

Testy parametryczne

Służą do weryfikacji hipotez parametrycznych, odnoszących się do parametrów rozkładu badanej cechy w jednej, dwóch lub kilku populacjach generalnych. Najczęściej weryfikowane są sądy dotyczące takich parametrów populacji jak: wartość oczekiwana, wariancja, wskaźnik struktury i współczynnik korelacji.

---