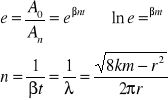1/V Amplituda drgań tłumionych w ciągu t₁=5min zmalała dwukrotnie. W jakim czasie zmaleje ośmiokrotnie w stosunku do amplitudy A_t1.

;

;

;

2/V Znaleźć logarytmiczny dekrement tłumienia wahadła matematycznego o długości l=50cm, jeżeli w czasie t=5min całkowita energia zmaleje n=4*10⁴ razy.

Drgania tłumione opisuje równanie

x(t)=A₀e^-βtsin(ωt+φ)

logarytmiczny dekrement tłumienia

całkowita energia drgania

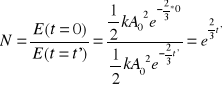
czyli

dla drgania tłumionego

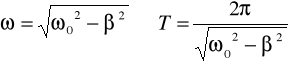
dla drgania nietłumionego wahadła matematycznego

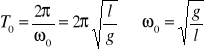
stąd dla drgania tłumionego wahadła

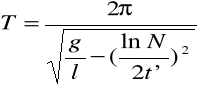
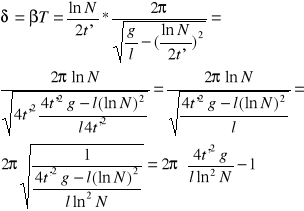
3/V wahadło matematyczne o długości l i logarytmicznym dekremencie tłumienia λ wykonuje drgania tłumione. Obliczyć ile razy zmaleje amplituda drgań po czasie τ.

Wahadło matematyczne o długości l

Okres drgań własnych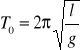

Częstość drgań własnych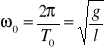

Logarytmiczny dekrement tłumienia

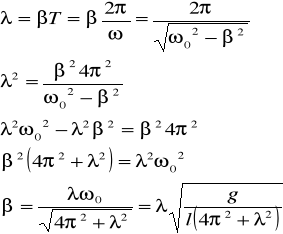
amplituda drgań po czasie τ

A=A₀e^-βτ

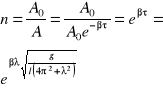
4/V W pewnym ośrodku wahadło matematyczne wykonuje drgania z logarytmicznym dekrementem tłumienia λ₀. jaki będzie logarytmiczny dekrement tłumienia λ, jeżeli opór ośrodka wzrośnie n razy. Ile razy należy zwiększyć opór ośrodka, aby wahadło przestało drgać.

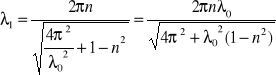
drgania zanikają gdy

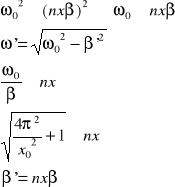
5/V naładowany kondensator o pojemności C wraz z cewką o znikomo małym oporze i indukcyjności L stanowią obwód drgający. Obliczyć okres wolno zanikających drgań w tym obwodzie.

Jeżeli V jest całkowitą zmagazynowaną energią w obwodzie to mamy:

V nie jest stałe
, gdzie znak minus oznacza, że zmagazynowana energia V maleje z czasem, zmieniając się w ciepło

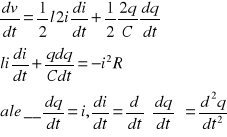
więc

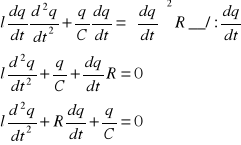
jest to równanie różniczkowe opisujące drgania tłumione w obwodzie LC. Równanie opisujące drgania tłumione masy na sprężanie

równania te są matematycznie identyczne rozwiązania przedostatniego przez analogie do rozwiązań ostatniego

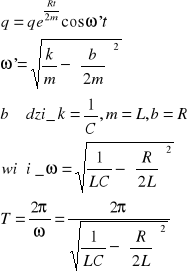
6/V obwód elektryczny składa się z pojemności C, indukcyjności L i oporu R połączonych szeregowo. W obwodzie tym odbywają się drgania tłumione. Obliczyć logarytmiczny dekrement tłumienia oraz dobroć tego obwodu.

Drgania tłumione w obwodzie RLC

λ - logarytmiczny dekrement tłumienia

β - współczynnik tłumienia

okres drgań tłumionych

ω - częstość drgań tłumionych

ω₀ - częstość drgań własnych

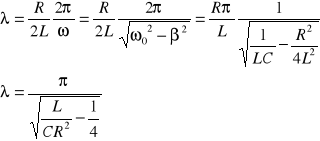
dobroć obwodu

ω_r - częstość rezonansowa

dla rezonansu natężeń

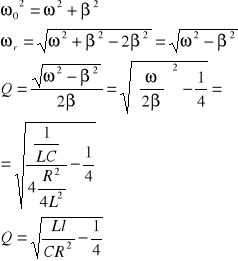
7/V Częstotliwość własna obwodu wynosi υ₀, a dobroć Q. W obwodzie wzbudzono drgania tłumione, według jakiej zależności będzie malała energia W tego obwodu z upływem czasu. Jaka część energii początkowej pozostanie po czasie τ?

Amplituda drgań tłumionych

A(t)=A₀e^-βt maleje wykładniczo z upływem czasu.

Energia zależy od kwadratu amplitudy

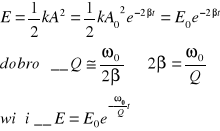
po czasie τ

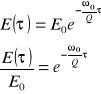
8/V ciało o masie m. zamocowane w naczyniu z lepką cieczą o współczynniku oporu r za pomocą dwu sprężyn o współczynniku sprężystości k każda. W chwili początkowej utrzymywane jest przez niezdeformowane sprężyny w pozycji równowagi. Ciało wychylamy z położenia równowagi. Obliczyć: a) współczynnik tłumienia β, b) czas relaksacji τ, c) częstotliwość drgań d) logarytmiczny dekrement tłumienia, e) liczbę drgań po których amplituda zmaleje e razy

połączenie równoległe sprężyn

siła działająca na ciało jest sumą sił pochodzących od obu sprężyn, a wychylenie sprężyn jest takie same.

F=F₁+F₂ k_wx=k₁x+k₂x

k_w=k₁+k₂

okres drgań ciała podwieszonego do sprężyny

czyli w naszym przypadku gdy: k₁=k₂=k

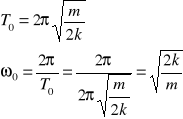
równanie drgań tłumionych

x=A₀e^-βtsin(ωt+φ)

A₀ - amplituda początkowa (t=0)

a) współczynnik tłumienia

r - współczynnik oporu cieczy

b) czas relaksacji

c) częstość drgań ω²=ω₀²-β²

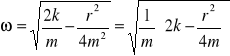
d) logarytmiczny dekrement tłumienia

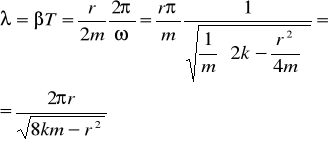
e) w czasie n drgań amplituda zmniejsza się od A₀ do A_n

A_n=A₀e^-βnt