Ćwiczenie 11- PROMIENIOWANIE TERMICZNE

Wykonanie ćwiczenia

1. przy pomocy wzorcowej lampy rtęciowej wyskalowałam położenie bębna spektroskopu w funkcji długości fali. W tym celu zmieniając położenie bębna znalazłam wszystkie wartości maksymalne prądu fotopowielacza, którym odpowiadają pewne długości fali.

2. w miejsce lampy rtęciowej i umieszczono żarówkę, a obwód zestawiono wg. Schematu załączonego w instrukcji. Dokonałam pomiaru mocy całkowitej P_c wydzielonej w obwodzie. W tym celu dokonałam pomiaru natężenia prądu w obwodzie. Zanotowałam opór wewnętrzny amperomierza i klasę mierników. Przy pomocy pirometru wyznaczyłam zależność temperatury T od prądu żarzenia żarówki I_ż. Do pomiaru użyłam filtr czerwony.

3. Wyznaczyłam zależność prądu fotopowielacza I_F od prądu żarzenia włókna I_ż dla trzech różnych długości fal. W tym celu wybrałam trzy długości fali - w okolicy maksimum, oraz po jednej z lewej i prawej strony i dla nich wykonałam pomiary.

Opracowanie wyników

1. Wykreśliłam krzywą skalowania spektroskopu
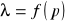
   . Wykres I.

2. Wykreśliłam zależność temperatury od T od natężenia prądu żarówki
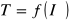
   . Zaznaczyłam niepewności pomiarowe.

3. Obliczyłam i umieściłam w tabeli:

• Opór włókna żarówki R_w uwzględniając opór wewnętrzny amperomierza r_A.

Korzystałam ze wzoru:

Wyniki zanotowałam w tabeli 1.

• Odczytałam z wykresu T=f(I_ż) brakujące wartości temperatury i umieściłam je w tabeli 1.

• Obliczyłam moc całkowitą P_c wydzieloną na włóknie, korzystając ze wzoru:

Wyniki umieściłam w tabeli 1.

• Sporządziłam wykres zależności P_c=f(R_w)

• Odejmując od wykresu P_c=f(R_w) część wynikającą z przewodnictwa cieplnego Z(R_w) obliczyłam wartości mocy wypromieniowanej przez włókno P_w i wpisałam do tabeli.

U [V]	I[A]	T*100 [C]	Rw[ ]	Pc [W]	Pw [W]
0,5	1,5	9	0,2583	0,75	-----
1	1,7	10	0,5662	1,7	-----
1,5	2	9,4	0,728	3	-----
2	2,4	13,5	0,8113	4,8	2
2,5	2,7	13,5	0,9039	6,75	3,5
3	3,1	16	0,9457	9,3	5,5
3,5	3,3	16	1,0386	11,55	7,5
4	3,6	17,8	1,0891	14,4	10
4,5	3,8	18	1,1622	17,1	12
5	4,1	19	1,1975	20,5	15,5
5,5	4,4	19,5	1,228	24,2	19,
6	4,6	21	1,2823	27,6	22,5

4. Korzystając z metody regresji liniowej obliczyłam współczynniki a i b funkcji lnPw=f(lnT)

oraz odpowiadające im odchylenia standardowe Sa i Sb.

a=5,04

b=-35,35

Sa=0,41

Sb=2,93

lp	T[C]	Pw[W]	lnT(x)	lnPw(y)	x^2	y^2	x*y
1	1350	2	7,21	0,69	51,95	0,48	5,00
2	1350	3,5	7,21	1,25	51,95	1,57	9,03
3	1600	5,5	7,38	1,70	54,43	2,91	12,58
4	1600	7,5	7,38	2,01	54,43	4,06	14,87
5	1780	10	7,48	2,30	56,02	5,30	17,23
6	1800	12	7,50	2,48	56,18	6,17	18,63
7	1900	15,5	7,55	2,74	57,00	7,51	20,69
8	1950	19	7,58	2,94	57,39	8,67	22,31
9	2100	22,5	7,65	3,11	58,52	9,69	23,82
suma	15430	97,5	66,93	19,25	497,87	46,37	144,14

Prosta teoretyczna:

y=5,04x - 35,35

y₁=4,63x-32,42

y₂=5,45x-38,28

Współczynnik a jest równy wykładnikowi potęgi n=4 w prawie Stefana-Boltzmana

Z moich obliczeń n = a, wynosi:

5.Na podstawie krzywej skalowania spektroskopu
odczytuję długości fali dla położeń p₁, p₂, p₃.

Dla p₁=91,3

Dla p₂=83

Dla p₃=100

6. wykorzystując wykres T=f(Iż) odczytałam temp. Odpowiadającą Iż.

Iż [A]	IF[ Dla	IF[ Dla	IF[ Dla	T[^0C]
2	0,05	0,05	0,05	1050
2,5	0,05	0,06	0,05	1300
3	0,14	0,13	0,11	1500
3,5	0,55	0,49	0,32	1700
4	1,6	1,52	0,83	1850
4,5	3,75	3,8	2,94	2000

7. Korzystając z metody regresji liniowej obliczyłam współczynniki a i b funkcji
oraz odchylenie standardowe Sa i Sb dla przyjętych długości fali.

Dla

8.Wyznaczyłam współczynnik C₂ występujący we wzorze Plancka

---