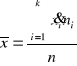
Zadanie 1.
n = 20 osób

X - czas pracy w latach od 0 do 12 lat

2 osoby mają X < 3

10 osób ma X < 6

18 osób ma X < 9

X max = 12

a) jaki był średni czas pracy w badanej grupie

xi	ni	nicum	xi	xini
<0;3>	2	2	1,5	3
<3;6>	8	10	4,5	36
<6;9>	8	18	7,5	60
<9;12>	2	20	10,5	21
Suma	20			120

To drugie x_i w tablece ma być z kółeczkiem nad x.

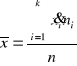
Interpretacja

Średni czas pracy w badanej grupie wynosił przeciętnie 6 [lat].

b) oceń asymetrię rozkładu stażu pracy w oparciu o wartość Pearsona

współczynnika skośności

W szeregu składającego się z przedziałów dominanty nie można

wyznaczyć, gdy dominująca liczebność występuje kilkakrotnie.

Liczebność = 8 (maksymalna) występuje dwukrotnie.

Wzór Pearsona:

Nie można do niego podstawić, bo nie można określić Dominanty,

a więc asymetrii tą miarą nie oszacujemy.

Zadanie 2.

	przyrosty	indeksy
	łańcuchowe	łańcuchowe
Lata	Yt-Y(t-1)	i t/t-1
2005	0,02	1,02
2006	0,03	1,03
2007	0,04	1,04
2008	0,05	1,05
2009	0,03	1,03
2010	0,01	1,01

a) o ile wzrosły ceny w Nibylandii w okresie od 2004 roku?

Z roku na rok przeciętnie ceny w Nibylandii rosły o 2,99 %.

b) pewien ekspert stwierdził, że średnie roczne tempo zmian cen w

Nibylandii w badanych latach wynosi dokładnie 3%. Czy ma rację?

Odpowiedź uzasadnij.
Odp. Tak, ma rację, gdyż o tyle przeciętnie rosło zjawisko poziomu cen.

Zadanie 3.
a) o ile procent wzrosły ceny i o ile procent spadla wartość produkcji

z okresu na okres

indeks cen Paschiego: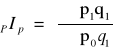
= 1,8 > 1 o 0,8= 80 %

Interpretacja:

Poziom cen wzrósł w okresie kolejnym w porównaniu do okresu

poprzedzającego o 80 % przy założeniu ilości z okresu kolejnego (badanego).

indeks wartości: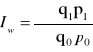
= 0,9 < 1 o 0,1

Interpretacja:

Wartość produkcji spadła w okresie kolejnym w porównaniu do okresu

poprzedzającego o 10 %.

b) oceń dynamikę zmian ilościowych w produkcji tej fabryki
Równość indeksowa dla indeksów agregatowych

= 0,5 < 1 spadek o 0,5 do 1.

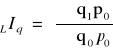
=1,0679

Interpretacja:

Poziom ilości spadł w okresie kolejnym w porównaniu do okresu

poprzedzającego o 50 % przy założeniu cen z okresu poprzedzającego.

Zadanie 4.
Y - zużycie benzyny w l/km

X - prędkość samochodu w km/h

Odchylenie standardowe dla obu cech:

- wariancja zużycia benzyny 1,96
- wariancja prędkości 36,0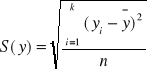

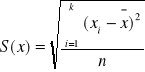
Kowariancja:

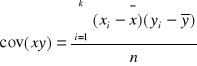
= 5,99

a) oceń siłę zależności korelacyjnej obu cech

[wsp. korelacji liniowej Pearsona]

Ocena siły korelacji (xy):

0,7

<0,9 korelacja dodatnia wysoka

Interpretacja:

Wartość współczynnika korelacji (
0,713) wskazuje, że między

cechą X a cechą Y zachodzi dodatnia wysoka korelacja. Wraz ze wzrostem X

wzrostowi podlega Y.

b) oceń kształt zależności zużycia benzyny względem prędkości samochodu

regresja Y względem X.

(wzór równania regr. liniowej cechy Y względem cechy X)

Oszacowane równanie regresji liniowej ma postać:

B - można obliczyć, jeśli będą podane wartości średnich.

Zadanie 5.
Oznaczenie:

Y - wynagrodzenie miesięczne

X - staż pracy

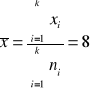
(Średnia arytmetyczna)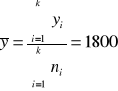

a) zapisz równanie regresji y względem x

(wzór równania regresji liniowej cechy Y względem cechy X)

- ze wzrostem stażu pracy o 1 rok wynagrodzenie wzrasta przeciętnie

o 120 zł a = 120.

Oszacowane równanie regresji liniowej ma postać:

b) ustal teoretyczne wynagrodzenie pracowników o 10-letnim stażu pracy

Y - wynagrodzenie miesięczne = ?

X - staż pracy = 10

Interpretacja

Teoretyczne wynagrodzenie pracowników o 10-letnim stażu pracy to 2040 zł.

1