Rodzaje pozycji

Podstawowe zasady prowadzenia nawigacji najłatwiej określić w kilku punktach, które warto sobie zapamiętać, jako przykazania:

"Jeśli jesteś pewien pozycji swego statku, sprawdź ją powtórnie, a gdy przekonasz się, że była prawidłowa, sprawdź ją koniecznie po raz trzeci !"

1. Podstawowym obowiązkiem nawigatora to znajomość aktualnej pozycji statku oraz granic jej błędu.

2. Należy jednak pamiętać, że prowadzenie nawigacji nie jest podstawowym obowiązkiem oficera wachtowego - nie przesiaduj mad mapą i dziennikiem, bądź na pokładzie, obserwuj widnokrąg i ruch statków, pilnuj wiatru i jakość sterowania przez sternika.

3. Na wachtę przychodź 5 minut przed jej objęciem, aby dokładnie zapoznać się z otoczeniem jachtu, a w nocy oswoić wzrok do ciemności, co jest bardzo ważne, szczególnie w czasie mgły. Prowadź na bieżąco, dokładnie i według instrukcji dziennik okrętowy. Absolutnie wszystko (łącznie z liczeniem) wpisuj najpierw do brudnopisu w porządku chronologicznym.

4. Nie ufaj zbytnio swojej pozycji obserwowanej (także z GPS-u), a tym bardziej pozycji zliczonej.

5. Pamiętaj o aktualizacji map i wydawnictw nawigacyjnych.
Używaj map najdokładniejszych, o możliwie największej podziałce. Zawsze miej przygotowaną mapę następnego akwenu morza w kierunku, którego płyniesz. Czytaj locje danych akwenów i portów.

6. Nie wymazuj nakresów z map aż do zakończenia rejsu, chyba.

7. Wyznaczaj pozycję, co godzinę lub częściej oraz zawsze przy każdej zmianie kursu.

8. Zapisuj w dzienniku współrzędne pozycji na koniec wachty oraz moment przekazania wachty.
W pobliżu przeszkód nawigacyjnych, w czasie złej pogody pozycję obserwowaną wyznaczaj przy każdej nadarzającej się okazji, czasem nawet, co kilka minut.

9. Nigdy nie namierzaj się na pławy (jedyne odstępstwo to latarniowce i pławy typu LANBY), dokładnie identyfikuj namierzane obiekty.

10. Jeżeli masz jakiekolwiek wątpliwości to natychmiast wzywaj kapitana!

11. Po wezwaniu kapitana i przejęciu przez niego prowadzenia jachtu, pamiętaj, że nikt nie zwalnia cię z obowiązku prowadzenia nawigacji i czynności związanych z bezpiecznym prowadzeniem statku.

Prowadzenie statku bezpieczną i możliwie najkrótszą drogą do punktu przeznaczenia wymaga od nawigatora stałej znajomości współrzędnych miejsca, w którym się on znajduje, czyli pozycji. W zasadzie rozróżnia się dwa rodzaje pozycji: zliczoną i obserwowaną. Istnieje jeszcze trzecia, rzadko wyznaczana w nawigacji pozycja prawdopodobna.

Pozycję zliczoną zapisuje się w ten sposób
, pozycję obserwowaną tak
.
U góry zapisuje się czas, zawsze czterocyfrowo bez kropki, na dole log, liczbą minimum trzycyfrową oddzielając ostatnia cyfrę przecinkiem. Gdy stan logu jest większy, np. 135,8 wpisuje się tylko 35,8 (całość jest wpisywana do dziennika okrętowego).

Nawigator powinien wykorzystać każdą sytuację, aby możliwie jak najdokładniej określić swoją pozycję. Taką okazją na pewno jest każdy, pojedynczy obiekt, który można namierzyć, (np. latarnia morska). Prowadząc nawigację, zawsze na mapie wykreślamy kurs, na którym w równych odstępach czasu, (co godzinę) nanosimy przebytą drogę odczytaną z logu. Tak otrzymujemy pozycje zliczone, czyli bardzo niedokładne pozycje. W momencie zauważenia jakiegoś obiektu, na który można się namierzyć (np. latarnia morska), robimy to bez zastanowienia.

Do określenia pozycji muszą być nam znane dwie wielkości (dwa parametry), które się nawzajem przecinają w jednym punkcie. Miejsce przecięcia się tych wielkości (parametrów) wyznacza nam pozycję.
Jak już wspomniano, pozycję nanosimy na mapę, jako punkt. Jednakże musimy mieć świadomość, że w praktyce pozycja nie jest punktem a zbiorem punktów na jakimś obszarze ograniczonym okręgiem, elipsą lub inna figurą geometryczną.

Wielkość tego obszaru zależy od:

• Błędu całkowitej poprawki.

• Błędu spowodowanego złym sterowaniem.

• Błędem spowodowanym niedokładnym określeniem przebytej drogi.

Długotrwałe obserwacje pozwalają empirycznie określić wielkość tego obszaru.

 

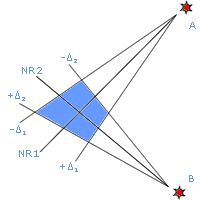
Pozycja zliczona (PZ) znajduje się gdzieś w obszarze zakreślonym na żółto. Parametry (-3) i (+3) oznaczają błędy sterowania.

 

• Pozycja zliczona
  Pozycję zliczoną otrzymuje się przez wykreślenie KDd z pozycji wyjściowej (np. z główek portu lub ostatniej pozycji obserwowanej) i odkładaniu na tej linii przebytej drogi. Co godzinę w rejsach morskich lub co cztery w rejsach oceanicznych. Pozycja otrzymana tą metodą nie jest dokładna z uwagi na błąd pomiaru przebytej drogi, błąd określenia dryfu, błędy sterowania oraz błąd całkowitej poprawki.

• Pozycja obserwowana
  Najprostszym sposobem określenia pozycji obserwowanej (zwanej też pozycją prawdziwą) jest dokonanie pomiarów (namiar, odległość, kąt poziomy) na wyróżniające się i zidentyfikowane obiekty lądowe o ściśle określonym położeniu (np. latarnie morskie), które naniesione są na mapy nawigacyjne. Pozycję obserwowaną otrzymuje się przez wykreślenie na mapie przynajmniej dwóch linii pozycyjnych. Punkt przecięcia dwóch linii pozycyjnych wyznacza pozycję obserwowaną.

• Pozycja prawdopodobna
  Pozycję prawdopodobną otrzymuje się przez wykreślenie na mapie tylko jednej linii pozycyjnej. W praktyce rzadko jest stosowana, ponieważ, na jeden punkt nawigacyjny można zrobić dwa namiary i wyznaczyć dwie linie pozycyjne gdzie już łatwo kreślić pozycję obserwowaną. Pozycją prawdopodobną jest punkt leżący na linii pozycyjnej najbliższy pozycji zliczonej. 

Linie pozycyjne

Linie pozycyjne maja tę właściwość, że pomiar tego samego parametru (kata pionowego, poziomego, namiaru) na którymkolwiek z punktów na takiej linii, da zawsze ten sam wynik.
a) linia pozycyjna z namiaru
b) linia pozycyjna z odległości (kąt pionowy, jako łuk)
c) linia pozycyjna z kąta poziomego (okrąg)
d) linia pozycyjna z sondowania (głębokości)
e) linia pozycyjna dla stałej różnicy odległości od dwóch stałych obiektów (hiperbola)

Linie pozycyjne dzielimy na:
1. dokładne
Są to linie, które nie wymagają poprawek. Robimy pomiar i bezpośrednio nanosimy go na mapę. Takimi liniami są:

• Nabieżnik, przeważnie są naniesione na mapie, ale możemy też sami nanieść nabieżnik na mapę. Wystarczy połączyć linią prostą dwa zidentyfikowane obiekty, zmierzyć jego kierunek i opisać.

• Okrąg, jako linia pozycyjna z kąta poziomego. Zmierzony kąt poziomy przy pomocy sekstantu jest tak dokładny, że nie jesteśmy w stanie wykreślić go na mapie. Wniosek - żadnej poprawki.

• Okrąg, jako linia pozycyjna z kąta pionowego. Tutaj, niestety musimy pamiętać o tym, że wysokości obiektów używanych do określenia pozycji odnoszą się do "zera mapy", co ma znaczenie w rejonach gdzie występują pływy. Na Bałtyku można przyjąć - brak pływów.

2. niedokładne
Są to linie, które przed ich wykreśleniem na mapie wymagają poprawek.

• Namiar kompasowy. Musi być poprawiony o całkowitą poprawkę.
  Całkowita poprawka to: deklinacja i dewiacja.
  Deklinacja wymaga uaktualnienia, ale mapę należy czytać z wielką uwagą. Są rejony, gdzie bardzo trudno określić deklinację z powodu zaburzeń magnetycznych, co jest naniesione na mapach. Te zaburzenia mogą być dosyć znaczne.
  Dewiacja. Praktycznie każdy rok powinna być określana od podstaw, tym bardziej, że ulega zmianie.
  Poza tym, dewiacja może się zmienić samorzutnie w czasie rejsu z różnych przyczyn. Suma tych poprawek jest wystarczająco duża, aby uznać "namiar kompasowy" za niezbyt dokładną linię pozycyjną.

Linie pozycyjne można wyznaczyć:

• Linia pozycyjna z namiaru - linią pozycyjną jest prosta (namiary opisano w

• Linia pozycyjna z odległości - linią pozycyjną jest okrąg.
  Najprostszym sposobem pomiaru odległości od obserwatora do obiektu (np. latarni morskiej), jest pomiar kąta pionowego α za pomocą sekstantu. Linią pozycyjną jest wtedy okrąg o promieniu równym tej odległości, zakreślony z punktu w którym znajduje się obiekt.

Mierząc kąt pionowy sekstansem należy doprowadzić do styku wierzchołka rzeczywistego obrazu z podstawą obrazu odbitego, manewrując odpowiednio alidadą. Odczytana wartość z podziałki sekstansu, poprawiona o błąd sekstansu i indeksu jest równa kątowi α. Znając wartość kąta pionowego α i wysokości obiektu można skorzystać z Tablic Nawigacyjnych i odczytać w odpowiedniej tablicy wynik, czyli odległość. Odległość można również obliczyć ze wzoru:

D - odległość obiektu (np. latarni morskiej) w milach morskich [Mm]; H - wysokość obiektu w metrach [m]; α - zmierzony kąt pionowy w minutach [']. Jeżeli kąt zmierzony jest w stopniach i minutach, stopnie zamieniamy na minuty.

• Linia pozycyjna z kata poziomego - linią pozycyjną jest łuk.
  Kąt poziomy β mierzy się sekstantem. Linia pozycyjna z kata poziomego mierzonego za pomocą sekstantu jest najdokładniejsza z uwagi dużą dokładność sekstantu wysokie wartości mierzonych kątów, no i przede wszystkim niezależność pomiaru od deklinacji i dewiacji. Ze względu na dokładność, kąt poziomy powinien zawierać się w granicach 030° - 150°. Czyli nie powinien być mniejszy od 30° i nie większy od 150°.

 Konstrukcja linii pozycyjnej z kąta poziomego

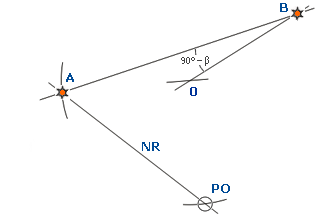
Zmierzyć kąt poziomy β pod jakim znajdują się obiekty A i B, wcześniej zidentyfikowane na mapie. Połączyć linią prostą obiekty A i B (na mapie) i z punktów A i B poprowadzić proste pod kątem (90° - β) w stosunku do prostej A B. Punkt 0 jest punktem przecięcia się tych prostych. Z punktu 0 zakreślić okrąg o promieniu A0 = B0. Łuk A P B tego okręgu jest, szukaną linią pozycyjną - rys.1

Gdy zmierzony kąt poziomy β będzie większy niż 90° , wartość (90° - β) stanie się ujemna i proste A0 i B0 należy poprowadzić po przeciwnej stronie linii A B w stosunku do obserwatora - rys.2
Jak wiadomo, nie ma ujemnych kątów. W tym wypadku znak "-" oznacza, że środek koła będzie się znajdował "od" nas, czyli po drugiej stronie linii łączącej dwa obiekty. Odwrotnie niż na rys.1, tam znak "+" oznacza, że środek koła jest "ku" nam, w naszym kierunku.

Gdy wartość zmierzonego kąta poziomego β wyniesie 90° wtedy punkt 0 z którego należy zakreślić okrąg leży w środku prostej A B - rys.3

 

Kąt poziomy można również uzyskać przez dokonanie dwóch namiarów, ich różnica będzie wtedy kątem poziomym. Jednak niedokładność wartości takiego kąta, skłania do wyznaczenia od razu pozycji obserwowanej z owych dwóch namiarów.

• Linia pozycyjna z głębokości - linią pozycyjną jest krzywa
  Linia pozycyjna z głębokości jest nie dokładna, ale w sytuacji, gdy nie ma możliwości wykreślenia innej może być przydatna.

 

W nawigacji pozycję można określić:

1.  z jednego obiektu

• namiar + odległość

• namiar + namiar (przesunięcie linii pozycyjnej)

• namiar + n-namiarów (wachlarz namiarów, określenie aktualnego znosu)

• namiar + głębokość

2.  z dwóch obiektów

• namiar + namiar

• namiar + kąt poziomy

• odległość + odległość

3.  z trzech obiektów

• namiar + namiar + namiar

• kąt poziomy + kąt poziomy

• odległość + odległość + odległość

• nabieżnik + namiar

4.   z więcej niż trzech obiektów (rzadko brane pod uwagę)

Mając do dyspozycji dwa obiekty, z których określamy pozycję, możemy otrzymać pozycję obserwowaną PO, ale z różnymi dokładnościami. Biorąc pod uwagę, czym określamy pozycję możemy przyjąć: namiernik i sekstant.

• Pozycja z dwóch namiarów kompasowych jest najmniej dokładna, ponieważ obciążona dużej ilości błędami (dewiacja, deklinacja), zarówno w pierwszym jak i drugim namiarze.

• Pozycja z namiaru kompasowego i kąta poziomego jest dokładniejsza od poprzedniej, ponieważ tylko jeden namiar jest obciążony błędem (dewiacja, deklinacja), natomiast pomiar kąta poziomego jest obciążony tak minimalnym błędem, że nie bierzemy go pod uwagę.

• Pozycja z dwóch kątów pionowych jest niebezpieczna, ponieważ z odległości np. 5 Mm możemy nie widzieć dokładnie podstawy mierzonego obiektu i albo go skrócić, albo wydłużyć, co natychmiast odbije się na odczycie odległości, a ta różnica może być dosyć duża.

Mając do dyspozycji trzy obiekty możemy otrzymać pozycję z dwóch kątów poziomych, która jest najdokładniejsza z uwagi na brak błędów (dewiacja, deklinacja). Pozycja z dwóch kątów poziomych jest dokładna do tego stopnia, że pomiaru nie jesteśmy w stanie tak dokładnie wykreślić na mapie, w stosunku jak go odczytaliśmy.

 

Dokładność pozycji obserwowanej z namiarów kompasowych

Aby przejść z KDd na KK musimy uwzględnić szereg poprawek:

• Całkowita poprawka (±cp) - deklinacja odczytana z mapy oraz dewiacja z tabeli, co praktycznie rozwiązuje problem.

• Poprawka na wiatr (±pw) - tu już jest problem, jeszcze nikomu nie udało się ustalić jaka jest dokładna wartość pw w żądanej chwili, wszystko zależy jak wiatr zawieje. Jedynie czego jesteśmy pewni to jej znaku "+" lub "-". O dziwo, poprawkę na wiatr najtrudniej określić można przy słabych wiatrach, rzędu 3 - 4° B. A więc można przyjąć, że pw jest poprawką na oko.

• Poprawka na prąd (±pp) - to samo co z wiatrem. Co prawda są rejony, gdzie prądy wykazano tabelarycznie, ale tak naprawdę to nikt głowy nie da, że to co w tabeli, jest akurat na morzu, łącznie ze znakiem "+" lub "-".

• Poprawka na sternika (±ps) - bez komentarza, chyba że w załodze jest sternik regatowiec.

• Poprawka na falowanie (±pf) - proszę utrzymać kurs KK chociaż przez 2 minuty, na fali.

Wynik każdego pomiaru zawsze jest obarczony pewnym błędem. Dotyczy to przede wszystkim wyznaczanych linii pozycyjnych z namiarów, a więc i pozycji obserwowanej (PO).
Jak widać na rysunku namiary NR1 i NR2 są obarczone błędami o maksymalnych wartościach ±Δ1 oraz ±Δ2
Pozycji obserwowanej nie wyznacza, więc punkt przecięcia się linii pozycyjnych z namiarów NR1 i NR2. Pozycja obserwowana leży gdzieś w obrębie zaznaczonego na niebiesko obszaru, a największa przekątna tego obszaru jest miarą błędu pozycji obserwowanej.
Pomijając wiele czynników takich jak deklinacja, dewiacja czy warunki atmosferyczne, w jakich nawigator wykonuje namiary, obszar, w którym znajduje się pozycja obserwowania będzie się zwiększał wraz ze wzrostem odległości do namierzanych obiektów. Zatem nawigator powinien umieć oszacować, z jakiej odległości najlepiej wykonać namiary dla zwiększenia dokładności pozycji obserwowanej.

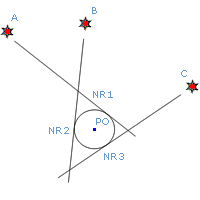
Jedną z metod ułatwiających ocenę dokładności pozycji obserwowanej (PO) jest dokonanie minimum trzech jednoczesnych namiarów. Wykreślone na mapie linie pozycyjne nie przetną się w jednym punkcie, ale utworzą tzw. trójkąt błędów (rysunek).

Małe rozmiary trójkąta świadczą o niewielkich błędach, przyjmuje się wtedy, że pozycją obserwowaną jest środek koła wpisanego w trójkąt błędów.

Duże rozmiary trójkąta spowodowane są większym błędem określenia przynajmniej jednej z linii pozycyjnych w stosunku do pozostałych dwóch. Pozycja obserwowana leży wtedy prawdopodobnie bliżej któregoś wierzchołka trójkąta błędów.

Wykreślenie trzech linii pozycyjnych z małą dokładnością może spowodować, że PO znaleźć się może poza trójkątem błędów!

Przykłady wyznaczania pozycji obserwowanej

 Pozycja obserwowana, najbardziej dokładna w nawigacji terestrycznej wymaga wyznaczenia przynajmniej dwóch linii pozycyjnych. W wypadku, kiedy linie pozycyjne określamy przy pomocy namiarów, linie te należy tak dobierać, aby kąt zawarty między nimi był większy od 030°, a mniejszy, od 150°, czyli mieścił się w granicach 030° - 150°

Pozycja obserwowana z dwóch namiarów jednoczesnych
Zrobić namiary na obiekty A oraz B w odstępie nie większym niż 1min i wykreślić na mapie namiary rzeczywiste. Punkt przecięcia się tych linii jest pozycją obserwowaną.

 

Pozycja obserwowana z dwóch namiarów niejednoczesnych
Zrobić namiar kompasowy NK na obiekt A. Poprawić NK, aby otrzymać NR1, i ten wykreślić na mapie. Punkt przecięcia się naszego kursu z namiarem daje pozycję prawdopodobną PP, którą opisujemy ułamkiem (czas w liczniku, stan logu w mianowniku). Od momentu zrobienia namiaru nie zmieniamy kursu i szybkości. Po jakimś czasie, kiedy namiar na oko na ten sam obiekt zmieni się więcej niż 030°, robimy drugi namiar na ten sam obiekt. Nanosimy na linię kursu przebytą drogę, odczytaną z logu, (PZ pozycja zliczona). Okazuje się, że linia pozycyjna z namiaru NR2 nie przechodzi przez punkt, w którym nanieśliśmy odczyt z logu (PZ), a przebiega obok. Jest to spowodowane błędami sterowania jak i wskazaniami logu (w wypadku, gdy nieznany jest współczynnik korekcyjny logu). Aby otrzymać pozycję obserwowaną PO, przesuwamy równolegle linię pozycyjną NR1 tak, aby przeszła przez PZ i przecięła linię pozycyjną NR2. Miejsce przecięcia się przesuniętej linii pozycyjnej NR1 z linią pozycyjną NR2 daje nam pozycję obserwowaną PO, z której dalej wykreślamy nasz kurs i po nim prowadzimy nawigację.

Wygodnie jest wykonać namiary w takich momentach by jeden był skierowany pod kątem 45° w stosunku do KDd a drugi był prostopadły do KDd. W chwili wykonywania drugiego namiaru odległość do mierzonego obiektu będzie równa przebytej drodze pomiędzy wykonanymi namiarami.

Jak to się robi:

• Na kursie KDd wyznaczyć PZ. Jak tylko znajdujemy się w zasięgu jakiegoś obiektu, z którego można określić PO, natychmiast to robimy.

• Wykonujemy pierwszy namiar, który nanosimy na mapę, jako NR1, jednocześnie nanosząc PZ.
  Uwaga: Punkt przecięcia się NR 1 z KDd nie jest naszą PZ.

• Wiadomo, że każda PZ posiada jakiś błąd, co ukazuje nam NR1. Wobec tego wstępnie mamy PP, która musi być wypośrodkowana między PZ a NR1. Namiar jest dokładniejszy, więc PP będzie się znajdowała na NR1 w punkcie jak najbliższym PZ.
  Czyli trzeba wyznaczyć prostopadłą do NR1 przechodzącą przez PZ (określoną w tym samym czasie, co NR 1)

• Punkt przecięcia się prostopadłej z NR1 wyznacza nam PP. Tym sposobem mamy wstępną najbardziej przybliżoną 'PO'

• Od PP wyznaczamy dalej nasz KDd (będzie to linia równoległa do poprzedniego KDd)

• Po jakimś czasie robimy drugi namiar i nanosimy go na mapę, jako NR2 i jednocześnie na nowej KDd odkładamy log w momencie zrobienia NR2.

• Następnie przenosimy NR1 równolegle do PZ'. Punkt przecięcia się NR2 z przeniesionym równolegle NR1' jest naszą PO.

 

Pozycja obserwowana z głębokości i namiaru
W sytuacji, gdy nie można skorzystać z innych metod wykreślenia linii pozycyjnych, pomiar głębokości (sondowanie dna) może być podstawą do jej wyznaczenia. Warunkiem jest ukształtowanie dna morskiego, by można było wykluczyć niejednoznaczność pomiaru. Jeżeli jest możliwość, dokładność takiej pozycji można zwiększyć wykonując namiar.

 

Pozycja obserwowana z nabieżnika i namiaru
Płynąc blisko brzegu często można wykorzystać nabieżniki do określenia pozycji.
Nabieżnikami są na ogół linie namiarowe naniesione na mapie, na podejściach do portów lub na wąskich przejściach - pomocne szczególnie pilotom morskim.
Jeżeli taki nabieżnik naniesiony jest na mapie nawigacyjnej, to nie ma problemu, bo już mamy linię pozycyjną, na której wystarczy się tylko znaleźć.

Jeżeli go nie ma, nanosimy go sami:

• Identyfikujemy dwa obiekty na brzegu, które są naniesione na mapie.

• Łączymy je liną i odczytujemy jak KDd i tak też opisujemy.

• Mamy gotową linię pozycyjną, jako NR, a co najważniejsze nie poprawiamy go.

• W momencie, kiedy się na niej znajdziemy wystarczy namierzyć się na jakiś trzeci obiekt i w ten sposób otrzymujemy pozycję obserwowaną PO.

Wadą takiego określenia pozycji jest to, że musi to robić na ogół dwoje ludzi. Jeżeli dłuższy czas płyniemy wzdłuż lądu, to możemy sobie przygotować na całej trasie tyle nabieżników na ile nam mapa pozwoli. Jest to dokładniejsza pozycja od pozycji określonej z dwóch namiarów kompasowych.

 

Pozycja obserwowana z kąta poziomego i namiaru
Sposób wykreślenia na mapie pozycji obserwowanej z namiaru i kąta poziomego, mając do dyspozycji jedynie trójkąty nawigacyjne i cyrkiel (przenośnik) nawigacyjny.

Dane: NR = 315°, kąt poziomy = 75°

Wykreślić NR na latarnię A.

• Połączyć prostą latarnie, obiekty A i B (długą linią ze względu na rozmiar trójkątów nawigacyjnych, aby swobodnie nimi operować).

• Z jednego z obiektów, np. latarni B względem wykreślonej prostej odmierzyć kąt 90° - 75° (90° - β) i wykreślić prostą.

• Tą samą czynność robimy w odniesieniu do drugiego obiektu, z tym że już nie wykreślamy prostej (bo nie jest potrzebna), a mały odcinek, tak aby przeciął prostą wykreśloną z obiektu B. W ten sposób otrzymujemy środek okręgu 0, z którego można wykreślić okrąg, jako linię pozycyjną. Ale tego nie robimy (nie mamy przecież szkolnego cyrkla, grafit i ostrze), zresztą linia pozycyjna jako okrąg nie jest nam teraz potrzebna.

• Do tej chwili mamy wykreślony NR i środek okręgu 0. Kolej na cyrkiel nawigacyjny. Odmierzamy odległość z punktu 0 do obiektu A lub B (promień okręgu). Następnie jedna nóżka na środek okręgu, a druga na linię NR i otrzymujemy pozycję obserwowaną PO.

 

 

Pozycja obserwowana z dwóch kątów poziomych

Pozycja z dwóch kątów poziomych (β) jest pozycją bardzo dokładną, nie wymaga żadnych poprawek, ponieważ odczytane wartości kątów poziomych zmierzonych przy pomocy sekstantu nie wymagają korekty z uwagi na dużą dokładność (praktycznie brak poprawek). Odczyty wartości mierzonych kątów są tak dokładne, że nie jesteśmy ich w stanie wykreślić na mapie, w stosunku jak je odczytaliśmy. I na tym polega dokładność tej pozycji. Nawet początkujący nawigator, przy pomocy trójkątów nawigacyjnych jest w stanie wykreślić pomierzone kąty poziome z dokładnością do 1/4 (ćwierć stopnia).
Kąt poziomy można też zmierzyć lornetką z podziałką artyleryjską.

Minimum teorii
Suma kątów w dowolnym trójkącie równa się 180°
Suma dwóch kątów w trójkącie prostokątnym równa się 90° i na tym będziemy się opierali wykreślając pozycję.
Pamiętamy, że "+" oznacza "ku" nam, a "-" oznacza "od" nas.

Pozycję obserwowaną z dwóch kątów poziomych możemy wyznaczyć, używając do tego:

• Protraktora - przyrząd nawigacyjny do szybkiego wykreślania na mapie pozycji statku, po dokonaniu namiarów dwóch kątów poziomych. Protraktor składa się z trzech ramion: środkowego - nieruchomego i dwóch zewnętrznych - ruchomych. Ramiona osadzone są na tarczy wyskalowanej od 000 do 180 w lewo i prawo. W środku na wspólnej osi jest mały otwór, przez który ołówkiem zaznaczamy pozycję na mapie. Ruchomymi ramionami ustawiamy odczytane kąty poziome w stosunku do ramienia nieruchomego. Następnie tak przesuwamy protraktor po mapie, aby każde z ramion pokryło się z odpowiednim obiektem (środkowe ze środkowym obiektem).
  Ołówkiem zaznaczamy punkt i opisujemy (czas i log), jeżeli płyniemy, lub (czas), jeżeli kotwiczymy.

• Trójkątów nawigacyjnych - Wyznaczanie pozycji obserwowanej za pomocą trójkątów nawigacyjnych.

• Identyfikujemy trzy obiekty (A, B, C), które bierzemy pod uwagę do pomiarów.

• Mierzymy między nimi kąty poziome
  β1 pomiędzy obiektami A i B
  β2 pomiędzy obiektami B i C
  Pamiętając, że zmierzony kąt poziomy nie powinien być mniejszy od 030° i nie większy od 150° (większe od 150° nie będą, ponieważ sekstanty są wyskalowane do max. 145°, a przeważnie, do 135°, więc z tą wartością kąta nie ma problemu).
  Obiekt D celowo pominięto ze względu na dokładność pozycji. Kąt zawarty między latarnią D i B jest bliski 030°

• Ze środkowego obiektu B prowadzimy proste poprzez zewnętrzne obiekty A i C. Na mapie linie rysujemy daleko po za obiekty, ze względu na rozmiary trójkątów nawigacyjnych.

• Następnie rysujemy prostopadłe linie do w/w prostych, od obiektów A i C. W którą stronę rysujemy prostopadłe linie decyduje wartość kąta uzupełniającego, czyli (90° - β). Jeżeli ma wartość "+" rysujemy "ku" nam, a jeżeli ma wartość "-" rysujemy "od" nas, czyli w przeciwną stronę.

• Położenie obiektów namierzanych oraz jachtu względem siebie, może doprowadzić do następujących przypadków:
  β₁<90 i β₂<90
  β₁=90 i β₂<90 oraz odwrotnie
  β₁>90 i β₂<90 oraz odwrotnie
  β₁=90 i β₂=90
  β₁>90 i β₂>90

• Po zmierzeniu kątów poziomych odejmujemy je od 90°

• Rozpatrujemy przypadek β₁ < 90° ; β₂ < 90°
  Dane: β₁ = 70° ; β₂ = 50°
  Obliczenie kątów dopełniających:
  β₁ dopełniający = (90° - 70°) = 20°
  β₂ dopełniający = (90° - 50°) = 40°
  mamy tu spełniony warunek β₁<90° i β₂<90° a to oznacza, że linie prostopadłe rysujemy "ku" nam, czyli od obiektów A i C w stronę jachtu, czyli na morze.

• Po obliczeniu kąta dopełniającego wykreślamy go w stosunku do linii prostej łączącej obiekty, wierzchołek kąta to obiekt środkowy.
  Uwaga: nie rysujemy całego ramienia kąta (linia przerywana), a jedynie mały odcinek przecinający odpowiednią prostopadłą.
  Otrzymane punkty X i Y są wierzchołkami naszych kątów poziomych.

• Punkty X i Y łączymy prostą, która powinna być dłuższa niż odcinek XY.

• Następnie rysujemy linię prostopadłą do prostej XY, ale tak, żeby przechodziła przez środkowy obiekt B (nie jest konieczne rysowanie całej prostej).

• Punkt przecięcia się prostej XY z narysowaną prostopadłą do obiektu B jest naszą pozycją obserwowaną PO

 

 

Przykłady przy różnych warunkach

Pozycja obserwowana z dwóch kątów poziomych przy warunkach:
β₁ = 90° ; β₂ < 90° lub odwrotnie.
Suma dwóch kątów w trójkącie prostokątnym równa się 90°.
Dane: β₁=90° ; β₂=30°
Obliczenie kątów dopełniających:
β₁ dop. = (90 - 90) = (±0)
β₂ dop. = (90 - 30) = (+60)

W przypadku, gdy β = 0 nie rysujemy linii prostopadłej z obiektu (A), kąt β ma punkt X na pozycji obiektu A, a więc pokrywa się z tym obiektem.




 

Pozycja obserwowana z dwóch kątów poziomych przy warunkach:
β₁ = 90° ; β₂ = 90°
Taka sytuacja mimo, że komfortowa dla nawigatora jest niestety bardzo rzadka, ale możliwa.
Dane: β₁ = 90° ; β₂ = 90°
Obliczenie kątów dopełniających:
β₁ dop. = (90 - 90) = (±0)
β₂ dop. = (90 - 90) = (±0)

Sytuacja jasna, nasze pomocnicze punkty X i Y, znajdą się na pozycjach obiektów A i C




 

Pozycja obserwowana z dwóch kątów poziomych przy warunkach:
β₁ > 90° ; β₂ < 90° lub odwrotnie.
Dane: β₁ = 100° ; β₁ = 60°
Obliczenie kątów dopełniających:
β₁ dop. = 90 - 100 = (-10)
β₂ dop. = 90 - 60 = (+30)
Jeden z kątów jest kątem ujemnym. Jak wiemy kątów ujemnych nie ma, toteż kąt dopełniający ma bezwzględną wartość 10, natomiast (-) jest dla nas wskazówką, że kąt jest poza układem. "Układ" jak pamiętamy to obszar znajdujący się między nami (jachtem), a obiektami namierzanymi (latarnie, wieże, kominy, itd.). Wobec tego z pozycji A rysujemy prostopadłą do linii łączącej A z B, ale w przeciwnym kierunku, czyli "od nas" lub inaczej "na zewnątrz układu". Dalej postępujemy identycznie jak w pozostałych przypadkach i wyznaczamy PO.




 

Pozycja obserwowana z dwóch kątów poziomych przy warunkach:
β₁ > 90° ; β₂ > 90°, czyli oba kąty rozwarte.
Dane: β₁ = 100° ; β₂ = 125°
Obliczenie kątów dopełniających:
β₁ dop. = 90 - 100 = (-10)
β₂ dop. = 90 - 125 = (-35)
Już wiemy, że oba kąty wyjdą poza układ, więc prostopadłe rysujemy "od siebie". Rysujemy ramiona kątów dopełniających, łączymy punkty X i Y. Następnie prostopadła do linii XY, przechodząca przez latarnię B. Przecięcie się prostopadłej z linią XY to nasza PO.




---