11. Obwody rozgałęzione prądu sinusoidalnego

1. Równanie macierzowe do obliczania obwodów prądu zmiennego metodą oczkową

Z x I₀ = E

Z₁₁ , Z₁₂ , . . . Z_1n - macierz impedancji własnych i wzajemnych

Z₂₁ , Z₂₂ , . . . Z_2n (macierz kwadratowa symetryczna):

Z= na głównej przekątnej występują impedancje

własne oczkowe (Z_kk), poza główną przekątną

impedancje wzajemne (Z_kl)

Z_n1 , Z_n2 , . . . Z_nn

Z_kk - impedancja własna k-tego oczka jest równa sumie impedancji wszystkich gałęzi należących do tego oczka. Impedancje własne oczek przyjmujemy zawsze ze znakiem (+).

Z_kl - impedancja wzajemna k-tego oczka z oczkiem l-tym jest równa impedancji gałęzi wspólnej oczka k-tego i l-tego. Znak impedancji wzajemnej zależy od zwrotów prądów oczkowych w gałęzi wspólnej. Jeżeli zwroty prądów oczkowych są zgodne to przyjmujemy znak (+), jeżeli przeciwne to znak (-).

I₀₁ - macierz prądów oczkowych (macierz kolumnowa)

I₀₂ o liczbie wierszy n równej liczbie oczek liniowo

niezależnych obwodów.

I_o =

I_on

E₁₁ - macierz napięć źródłowych oczkowych (macierz kolumnowa)

E₂₂ o liczbie wierszy n równej liczbie oczek liniowo niezależnych obwodów.

E =

E_kk - napięcie źródłowe k-tego oczka jest równe sumie napięć źródłowych gałęzi nieleżących do k-tego oczka.

E_nn

2. Równanie macierzowe do obliczania obwodów prądu zmiennego metodą potencjałów węzłowych

Y x V = I_źr

Y₁₁, Y₁₂ , . . . Y_1n - macierz admitancji własnych i wzajemnych

Y₂₁, Y₂₂ , . . . Y_2n (macierz kwadratowa symetryczna): na głównej

Y = . przekątnej występują admitancje własne węzłów . ze znakiem (+), poza główną przekątną (-).

Y_n1 , Y_n2 , . . . Y_nn

V₁

V₂ - macierz napięć węzłowych (macierz kolumnowa) o liczbie wierszy równej n , tzn. liczbie n węzłów liniowo niezależnych.

V = .

.

Vn

I_źr1

I_źr2 - macierz prądów źródłowych wypadkowych w węzłach

. (macierz kolumnowa) o liczbie wierszy n równej liczbie

I_źr = . węzłów liniowo niezależnych.

.

I_źrn

Twierdzenie Thevenina

Każdy dowolny aktywny obwód liniowy można od strony wybranych dwóch zacisków ab zastąpić obwodem równoważnym złożonym z połączonego szeregowo jednego idealnego napięcia E_z i jednej idealnej impedancji zastępczej Z_z.

Z_z

I

Z - impedancja odbiornika

Z

E_z

I = E_z / [Z_z + Z]

Napięcie zastępcze E_z jest równe napięciu, jakie wystąpi na zaciskach ab po odłączeniu odbiornika o impedancji Z , tzn w stanie jałowym.

Impedancja zastępcza Z_z jest równa impedancji, widzianej z zacisków ab po zwarciu wszystkich źródeł napięcia i rozwarciu wszystkich źródeł prądu.

Twierdzenie Nortona

Każdy dowolny aktywny obwód liniowy można od strony wybranych dwóch zacisków ab zastąpić obwodem równoważnym złożonym z połączonego równolegle jednego idealnego źródła prądu I_żr oraz jednej admitancji zastępczej Y_z.

I_źr = E_z / Z_z , Y_z = 1 / Z_z Y - admitancja odbiornika

I

I_źr Y_z Y

I = {Y / [Y + Y_z]} I_źr

Prąd źródłowy zastępczego źródła prądu I_źr jest równy prądowi zwarcia I_z zacisków ab, do których dołączony jest odbiornik.

Admitancja zastępcza Y_z jest równa admitancji widzianej z zacisków ab po zwarciu wszystkich źródeł napięcia i rozwarcia wszystkich źródeł prądu.

METODA KLASYCZNA

Zadanie 1

Oblicz wartości symboliczne prądów gałęziowych w przedstawionym obwodzie prądu sinusoidalnego stosując metodę klasyczną ( równań Kirchhoffa).

Ustalamy liczbę węzłów w = 4.

Ustalamy liczbę niezależnych węzłów m = w - 1 = 4 - 1 = 3.

Wniosek. Możemy napisać 3 niezależne równania zgodnie z I prawem Kirchhoffa dla wybranych węzłów (np. 1, 2, 3).

Ustalamy liczbę gałęzi g = 6.

Ustalamy liczbę oczek niezależnych.

n = g - m = 6 - 3 = 3

Wniosek. Możemy napisać 3 niezależne równania zgodnie z II prawem Kirchhoffa dla wybranych 3 oczek.

Z I p. Kirchhoffa

Dla 1 węzła I = I₁₂ + I₁₃ -I + I₁₂ + I₁₃ = 0

Dla 2 węzła I₁₂ = I₂₃ + I₂₄ => -I₁₂ + I₂₃ + I₂₄ = 0

Dla 3 węzła I₂₃ + I₁₃ = I₃₄ -I₁₃ -I₂₃ + I₃₄ = 0

Z II p. Kirchhoffa

Dla 1 oczka I₁₂ x Z_L + I₂₄ x Z_L = U

Dla 2 oczka I₂₃ x Z_C + I₃₄ x Z_C - I₂₄ x Z_L = 0

Dla 3 oczka I₁₃ x Z_R - I₂₃ x Z_C - I₁₂ x Z_L = 0

Grupujemy odpowiednio 6 równań

-I + I₁₂ + I₁₃ + 0 x I₂₃ + 0 x I₂₄ + 0 x I₃₄ = 0

0 x I - I₁₂ + 0 x I₁₃ + I₂₃ + I₂₄ + 0 x I₃₄ = 0

0 x I + 0 x I₁₂ - I₁₃ - I₂₃ + 0 x I₂₄ + I₃₄ = 0

0 x I + Z_L I₁₂ + 0 x I₁₃ + 0 x I₂₃ + Z_L x I₂₄ + 0 x I₃₄ = U

0 x I + 0 x I₁₂ + 0 x I₁₃ + Z_C x I₂₃ - Z_L x I₂₄ + Z_C x I₃₄ = 0

0 x I - Z_L I₁₂ + Z_R I₁₃ - Z_C x I₂₃ + 0 x I₂₄ + 0 x I₃₄ = 0

stąd równanie macierzowe

-1 +1 +1 0 0 0 I 0

0 -1 0 1 1 0 I₁₂ 0

0 0 -1 -1 0 1 I₁₃ = 0

0 Z_L 0 0 Z_L 0 I₂₃ U

0 0 0 Z_C - Z_L Z_C I₂₄ 0

0 - Z_L Z_R - Z_C 0 0 I₃₄ 0

Rozwiązywanie układu 6 równań liniowych z 6-cioma niewiadomymi dla prądów gałęziowych uzyskamy korzystając z wzorów Cramera. Jednak przy 6 niewiadomych obliczenia są dość pracochłonne.

Pierwsze prawo Kirhoffa

Dla każdego węzła obwodu elektrycznego suma prądów dopływających do węzła jest równa sumie prądów odpływających od węzła.

ΣI_d = ΣI_odp

Drugie prawo Kirhoffa

W dowolnym oczku obwodu elektrycznego suma algebraiczna napięć odbiornikowych oraz suma algebraiczna napięć źródłowych jest równa zero.

ΣZ I + ΣE = 0

Zadanie 2

Oblicz wartość prądu I płynącego przez odbiornik o impedancji Z w obwodzie prądu sinusoidalnego stosując twierdzenie Thevenina oraz zasadę superpozycji do obliczania napięcia stanu jałowego E_z

Z₁ E₂

I

Z

E₁ Z₂

I_źr

Dane: E₁ = 10V , E₂ = j20V

Z₁ = 5 + j5 Ω , Z₂ = 5 -j5 Ω , Z = 5 Ω

I_źr = 4A

I = E_z / [Z_z + Z]

Do wyznaczenia prądu I zastosujemy twierdzenie Thevenina

1 / Z_z = 1 / Z₁ + 1 / Z₂ = [Z₂ + Z₁] / Z₁ Z₂ = [(5 + j5) + (5 - j5)] /

[(5 + j5) x (5 - j5)] = 10 / (25 + 25) = 10 / 50

Z_z = 5 [Ω]

^`'

Napięcie zastępcze E_z, napięcie stanu jałowego, obliczymy korzystając z zasady superpozycji.

A B

E_z = E_z' + E_z”

Dla schematu A:

a)

I_o^' x Z₁ + E₂ + I_o' x Z₂ - E₁ = 0

I₀'(Z₁ + Z₂) = - E₂ + E₁

I_o`= [E₁ - E₂ ] / [Z₁ + Z₂] = [10 - j20] / {[5+j5] [5-j5]} = [10 - j20] /10

I₀' = 1 - 2j [A]

b)

-E_z' = E₂' + I₀' x Z₂ = j20 + (1 - j2) (5 - j5)=

= j20 + 5 - j5 - 10j - 10 = -5 + j5

- E_z' = -5 + j5

czyli: E_z' = 5 - j5 [V]

Dla schematu B

Z I prawa Kirchoffa

a)

I_x + I_źr = I₀”

I_x = I₀” - I_źr

b)

I_x Z₂ + I₀” Z₁= 0

(I₀” - I_źr ) Z₂ + I₀” x Z₁ = 0

I₀” (E_z Z₂ + Z₁) = I_źr x Z₂

I₀” = [I_źr x Z₂] / [Z₂ + Z₁] = { 4 x [5 - j5]} / {[5 - j5] + [5 + j5]} =

= {20 -j20} / 10 = 2 - j2

I₀” = 2 - 2j [A]

c)

E_z” = I₀” x Z₁ = (2 - 2j)(5 + j5) =

= 10 + 10j - 10j + 10 = 20 [V]

E_z”= 20 [V]

E_z = E_z' + E_z” = 5 - j5 + 20 = 25 - j5 [V]

I = E_z / [Z_z + Z] = [25 -j5] / [5 + 5] = [25 - j5] / 10 = 2,5 -j 0,5

I_z= 2,5 - j0,5 [A]

Zadanie 3

Oblicz wartość prądu I płynącego przez odbiornik o impedancji Z w obwodzie prądu sinusoidalnego stosując twierdzenie Nortona oraz zasadę superpozycji do obliczania prądu zwarcia I_z.

Z₁ E₂

I

Z

E₁ Z₂

I_żr

Dane :E₁ = 10 [V], E₂ = j20 [V]

Z₁ = 5 + j5 [Ω], Z₂ = 5 - j5 [Ω], Z = 5 [Ω]

I_źr = 4 [A]

Do wyznaczenia prądu I zastosujemy twierdzenie Nortona.

I_źr Y_z Y

I = {Y / [Y + Y_z]} I_źr

I_źr = I_z

Obliczamy admitację zastępczą Y_z

Y₁

Y_z

Y₂

1 1 5 - j5 5 - j5 5 - j5

Y₁ = Z₁ = 5 + j5 = (5 + j5)(5 - j5) = 25 + 25 = 50 =

=0,1 - j0,1 [S]

1 1 5 + j5 5 + j5

Y₂ = Z₂ = 5 - j5 = (5 - j5)(5 + j5) = 50 = 0,1 + j0,1 [S]

Y_z = Y₁ + Y₂ = 0,1 - j0,1 + 0,1 + j0,1 = 0,2 [S]

Obliczamy wartości prądu zwarcia I_z korzystając z zasady superpozycji.

a) b) c)

Dla obwodu a)

E₂+ I_z' Z₂ = 0

I_z' = - E₂ / Z₂ = -j20 / (5 -j5) = -j20(5 +j5) / {[(5 -j5) (5 +j5)]}

= 2 - j2 [A]

Dla obwodu b)

E₁+ I_z” Z₁ = 0

- E₁ -10 -10(5 - j5)

I_z”
= Z₁ = 5 + j5 = 50 = (-1 + j) [A]

Dla obwodu c)

I_z”' = I_źr = 4[A]

Prąd zwarcia I_z.

I_z = I_z' + I_z” + I_z ^`'' = (2 - 2j) + (-1 + j) + 4 = (5 - j) [A]

Prąd ten przepływa przez gałąź ab w przypadku zwarcia zacisków ab, natomiast admitancja Y_z jest admitancją zastępczą sieci pasywnej widzianej z zacisków ab przy przerwie w gałązi ab.

Prąd I_źr zastępczego źródła prądu jest zatem prądem zwarcia gałęzi ab. Mając I_z oraz Y_z obliczamy prąd I w odbiorniku o admitancji Y = 1 / Z

I = {Z_z / ( Z_z + Z)} I_z = {Y / (Y + Y_z)} I_z

Obliczamy admitancję zastępczą Y_z.

Y₁

Y_z

Y₂

1 1 5 - j5 5 - j5 5 - j5

Y₁ = Z₁ = 5 + j5 = (5 + j5)(5 - j5) = 25 + 25 = 50 = 0,1 - j0,1 [S]

1 1 5 + j5 5 + j5

Y₂ = Z₂ = 5 - j5 = (5 - j5)(5 + j5) = 50 = 0,1 + j0,1 [S]

Y_z = Y₁ + Y₂ = (0,1 - j0,1) + (0,1 + j0,1) = 0,2 [S]

Y = 1 / Z = 1/5 = 0,2 [S]

stąd

I = {Y / [Y + Y_z]} I_z = {0,2 / (0,2 + 0,2)} (5 + j) = 0,5 (5 + j) =

= 2,5 + j0,5 [A]

Zadanie 4

Oblicz wartość prądu I płynącego przez amperomierz stosując twierdzenie Thevenina.

Dane:

I₁ I₂

Z₁ = 1 + j

Z₂ = 2 - j2

Z₁ Z₃ U₃ Z₃ = 1 - j

Z₄ = 2 + j2

U = 10V

U I

Z₄ U₄

Z₂

Napięcie zastępcze E_z obliczamy jako napięcie na zaciskach ab w stanie jałowym, tzn przy odłączonym amperomierzu.

U 10 10 10(3 + j1) 10(3 + j1)

I₁ = Z₁ + Z₂ = (1 + j)(2 - j2) = 3 - j1 = (3 - j1)(3 + j1) = 10 = 3 + j1 =

= (3 + j1) [A]

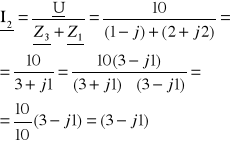
[A]

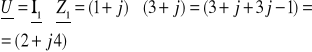
[v]

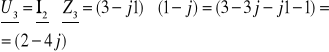
[v]

Obliczamy impedancję zastępczą Z_z widzianą z zacisków ab przy rozwarciu źródła zasilania

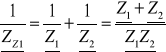
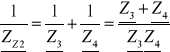
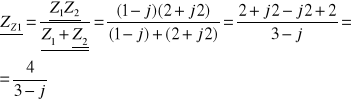
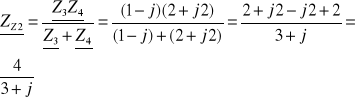
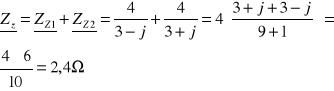
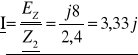
[A]

13

E_z

+

Ⴚ

4

3

2

1

2

1

3

2

1

3

I

I₃₄

C

C

L

L

R

I₂₄

I₂₃

I₁₃

I₁₂

U

4

3

2

1

Z₁

E₁

E₂

Z₂

I_źr

E₁

Z₁

E₂

Z₂

E_z'

I₀'

Z₁ I₀”

Z₂

I_źr

E_z''

Z₁

Z₂

Z_w

Z_z

E_z

I

Z

I_z

Z₁

E₁

E₂

Z₂

I_źr

Z₁

Ⴚ

+

+

I_z'''

Z₂

I_źr

I_z''

Z₁

E₁

Z₂

I_z'

Z₁

E₂

Z₂

_Z

Z₁

Z₃

Z₄

Z₂

I

a

b

d

c

---