Teoria sterowania

Laboratorium

Projektowanie liniowych układów dynamicznych w przestrzeni stanów, sterowalność i obserwowalność liniowych układów dynamicznych

Rafał Dobosz

gr. 23 A

rok II WIMiR

1. Cel ćwiczenia

- modelowanie układów dynamicznych w przestrzeni stanów,

- badanie sterowalności i obserwowalności liniowych układów dynamicznych.

2. Modelowanie układu dynamicznego:

- wielkość wejściowa: U_w

- wielkość wyjściowa: U_L

- R=10Ω, L=1H, C=2F

,
,

,

Wykres odpowiedzi dla powyższego schematu:

3.Modelowanie układu dynamicznego w przestrzeni stanów.

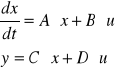
gdzie: x1=i , x2= Uc , y= UL , u= UW

Zapisanie równań stanu i wyjścia w postaci macierzowej:

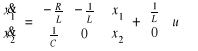
Następnie wykorzystując blok State-Space w pakiecie Simulink, po wpisaniu odpowiednich macierzy otrzymano wykres:

Jak widać odpowiedź pokrywa się z wykresem uzyskanym za pomocą poprzedniej metody. Rozwiązania obydwoma sposobami dają taki sam efekt.

3.Badanie sterowalności.

W programie Matlak macierz sterowalności możemy otrzymać za pomocą komendy Qs=ctrb(A,B), gdzie A,B - macierze parametrów układu

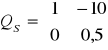
Kod programu Matlab:

A=[-10 -1;0.5 0];

B=[1;0];

Qs=ctrb(A,B);

rank(A)

rank(Qs)

Komendy rank(A) i rank(Qs),posłużyły do obliczenia rzędów macierzy A i Qs. W obu przypadkach rząd ten wyniósł 2, tak więc układ jest w pełni sterowalny.

4.Badanie obserwowalności.

Za pomocą komendy Qs=obsv(A,C) w programie Matlab, otrzymujemy macierz sterowalności dla zadanych wyjść układu:

a) wyjściem układu jest U_L

Kod programu Matlab:

A=[-10 -1;0.5 0];

C=[-10 -1];

Qo=obsv(A,C);

rank(Qo)

,

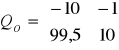
Za pomocą komend rank(Qs) otrzymujemy wartość rzędu macierzy Qs. Podobnie jak rząd macierzy A wynosi on 2, więc układ jest w pełni obserwowalny.

b) wyjściem układu jest U_C

Kod programu Matlab:

A=[-10 -1;0.5 0];

C=[0 1];

Qo=obsv(A,C);

rank(Qo)

,

Podobnie jak w podpunkcie a) rząd macierzy Q_O (=2) jest równy rzędowi macierzy A, więc układ jest w pełni obserwowalny.

---