Inżynieria materiałowa (laboratoria IWN)				Grupa dziekańska	E1
Temat:	Badanie pętli histerezy magnetycznej ferromagnetyków			Nr ćw.	5
Imię i nazwisko				Grupa laborat.	2
Data wykonania:	03.12.2009	Data oddania:	17.12.2009	Ocena:

1. Wprowadzenie teoretyczne

1.1 Pole magnetyczne

W uproszczeniu pole magnetyczne jest obszarem w którym na poruszające się, naładowane cząstki działa siła zależna od iloczynu ładunku i prędkości. Poruszające ładunki wytwarzają pole magnetyczne opisane wektorowo wielkościami: indukcji magnetycznej
, natężenia pola magnetycznego
i polaryzacją magnetyczną
. Występujące w ciałach stałych trwałe momenty magnetyczne pod działaniem zewnętrznego pola magnetycznego ulegają uporządkowaniu, materiał podlega namagnesowaniu inaczej polaryzacją magnetyczną. Namagnesowanie magnetyka jest wprost proporcjonalnego do pola makroskopowego, opisanego przez wektor indukcji magnetycznej wewnątrz ciała stałego , jest proporcjonalne do natężenia pola magnetycznego:

gdzie: μ₀ - bezwzględna przenikalność magnetyczna próżni równa 4μ*10^-7 [H/m], μ - względna przenikalność magnetyczna materiału

1.2 Ferromagnetyki

Dla większości ciał stałych μ ma wartość zbliżoną do 1, zatem wykres funkcji B=f(H) jest prostą przechodzącą przez początek układu współrzędnych, namagnesowanie podczas braku pola jest zerowe. Szczególną klasę pośród diamagnetyzmu i paramagnetyzmu stanowią ferromagnetyki, o μ wynoszącym rzędu 10³-10⁴ oraz silnie zależącego od natężenia zewnętrznego pola magnetycznego. W ferromagnetyku, momenty magnetyczne na skutek spontanicznego namagnesowania ustawiają się równoległe wzdłuż jednego kierunku tworząc obszar zwany domeną magnetyczną. W ciele stałym występuje wiele domen magnetycznych ustawionych w różnych kierunkach, konfiguracja w krysztale jest taka że energia całkowita osiąga minimum. Magnesowanie ferromagnetyka powoduje zmiany w strukturze domen, tj. przesuwanie granic i obrót domen. Każdy ferromagnetyk ma określoną temperaturę Curie zależną od materiału, po przekroczeniu tej temperatury zmienia właściwości ferromagnetyka i staje się paramagnetykiem.

1.3 Krzywa namagnesowania

Rzeczywista krzywa namagnesowania wyznacza się przez równoczesny pomiar indukcji magnetycznej B oraz natężenia zewnętrznego pola H. Kształt krzywej namagnesowania zależy m.in. od warunków początkowych i kierunku zmienności pola (zwiększenie lub zmniejszenie). Zwykle rozpoczyna się ono od stanu idealnego namagnesowania. Krzywa rozpoczynająca się w początku układu, odpowiadająca monotonicznemu wzrostowi natężenia pola podczas pierwszego namagnesowania, nazywa się krzywa pierwotnego. Pełne przemagnesowanie, czyli zmiana natężenia od Hmax do -Hmax i z powrotem do Hmax, odbywa się wzdłuż krzywej zamkniętej: pętla histerezy.

Współrzędne punktów przecięcia pętli histerezy z osiami układu współrzędnych sa punktami charakterystycznymi: Br - indukcja resztkowa, Hc - natężenie koercji. Wartość koercji jest podstawą podziału ferromagnetyków na materiały magnetyczne miękkie o małej koercji (zwykle poniżej 100 A/m) i materiały twarde o dużej koercji.

2. Zasada pomiaru i opis czynności

2.1 Zasada pomiaru

Jednym ze sposobów obserwacji pętli histerezy jest zastosowanie oscyloskopu. Układ pomiarowy musi być tak dobrany, aby wytwarzał sygnał napięciowy proporcjonalny do pola H (podawany jest on na płytki odchylające X) i sygnał napięciowy proporcjonalny do pola B (podawany na płytki odchylające Y). Układ pomiarowy zestawia się jak pokazano na rysunku:

Rys. 1 Schemat układu pomiarowego

Układ zasilamy prądem przemiennym, zatem na ekranie oscyloskopu uzyskamy pętle histerezy magnetycznej zgodnie z poniższym rysunkiem.

Rys. 2. Sposób wzorcowania pętli histerezy magnetycznej

2.2 Czynności:

1. Zestawienie układu pomiarowego zgodnie z schematem z rysunku 1.

2. Kalibracja/ustawienie parametrów pracy oscyloskopu (w trybie X-Y).

3. Ustawienie autotransformatora w punkcie zerowym, włączenie zasilania układu pomiarowego.

4. Dobranie wartości napięcia za pomocą autotransformatora tak, aby przy odpowiednio dobranych czułościach wzmacniacza kx i ky uzyskać dla badanego materiału na ekranie oscyloskopu pętle histerezy B(H).

5. Wykonanie pomiarów, odczytanie charakterystycznych punktów pętli histerezy dla rdzenia wykonanego z trzech badanych materiałów: xc, xmax, x'max, yr, ymax, y'max .

6. Wykonanie wykresów na podstawie pomiarów i obserwacji pętli histerezy (charakterystyka B(H)), aproksymowanie przebiegu charakterystyki indukcji magnetycznej w próżni B0(H) i indukcji namagnesowania materiału B_w(H).

7. Obliczenie potrzebnych wartości.

8. Wyciągnięcie wniosków końcowych.

3. Obliczenia tablice wykresy

3.1 Wzory obliczeniowe

Przykładowe dla blachy anizotropowej

H_max=
=

H_c=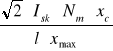
=

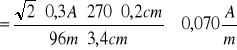
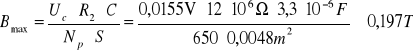
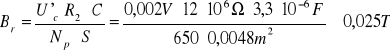
3.2 Tabele pomiarowo obliczeniowe

Tabela 3.1 Parametry badanych materiałów

Badany materiał	Pole przekroju poprzecznego rdzenia S[m2]	Liczba zwojów uzwojenia pierwotnego (magnesującego) Nm	Liczba zwojów uzwojenia wtórnego (pomiarowego) Np.	Długośc uzwojenia l [m]
Blacha anizotropowa	0,0048	270	650	96
Blacha izotropowa	0,0027	150	4000	368
Ferryt	0,0013	200	1000	58

Tabela 3.2 Wartości mierzone i obliczone parametrów pętli histerezy magnetycznej

Badany materiał	Isk [A]	kx [V]	ky [mV]	Uc [mV]	U'c [mV]	R2 [MΩ]	C [μF]	Hmax [A/m]	Hc [A/m]	Bmax [T]	Br [T]	Xc [cm]	Xmax [cm]	Yr [cm]	Ymax [cm]	X'max [cm]	Y'max [cm]
Blacha anizotropowa	0,3	10	5	15,5	2	12	3,3	1,193	0,070	0,197	0,025	0,2	3,4	0,4	3,1	4,2	3,2
Blacha izotropowa	0,25	10	10	25	13	12	3,3	0,144	0,015	0,092	0,048	0,3	2,8	1,3	2,5	3,4	2,6
Ferryt	0,4	10	1	1,5	1,2	12	3,3	1,951	0,900	0,046	0,037	1,2	2,6	1,2	1,5	4	1,6

Tabela 3.3 Wartości mierzone i obliczone dla jednego materiału i różnych Isk

Badany materiał	Isk [A]	kx [V]	ky [mV]	Uc [mV]	U'c [mV]	R2 [MΩ]	C [μF]	Hmax [A/m]	Hc [A/m]	Bmax [T]	Br [T]	Xc [cm]	Xmax [cm]	Yr [cm]	Ymax [cm]	X'max [cm]	Y'max [cm]
Blacha izotropowa   *pkt 6	0,02	2	5	9	6,5	12	3,3	0,012	0,007	0,033	0,024	0,7	1,1	1,3	1,8	1,1	1,8
				0,05					13	9			0,029	0,013	0,048	0,033	0,8	1,8	1,8	2,6	1,8	2,6
				0,1					17	11			0,058	0,015	0,062	0,040	1	3,8	2,2	3,4	4	3,5
				0,14					18,5	11,5			0,081	0,018	0,068	0,042	1,1	4,8	2,3	3,7	4,9	3,8

3.3 Wykresy B(fH)

Wykresy wykonane na papierze milimetrowym dla trzech badanych materiałów z aproksymowanymi B0(H) i Bw(H) oraz jeden dla blachy izotropowej dla różnych Isk

Wykres 1 - dla blachy anizotropowej

Wykres 2 - dla blachy izotropowej

Wykres 3 - dla ferrytu

Wykres 4 - dla blachy izotropowej dla czterech różnych Isk

4. Wnioski końcowe

1. Po osiągnięciu przez namagnesowany materiał stan nasycenia, w pętli histerezy wzrasta tylko składowa B₀(H), natomiast B_w(H) pozostaje stała.

2. Szeroka pętla histerezy wiąże się ze stratami mocy, im większe jest pole powierzchni taj pętli tym większa potrzebna jest energia na przemagnesowanie rdzenia.

3. Magnetyki dzielimy na twarde lub miękkie, zależnie od wykresu pętli histerezy. Im pętla szersza tym badany materiał jest twardszy.

4. Blacha anizotropowa jest materiałem miękkim, ponieważ ma wąską pętlę histerezy, szybko się namagnesowuje i rozmagnesowuje, namagnesowanie jest nietrwałe.

5. Podobnie do blachy anizotropowej, blacha izotropowa jest materiałem miękkich, jednak pętla histerezy jest nieco szersza, większa ilość krzemu polepsza trwałość i zwiększą przenikalność magnetyczną względną.

6. Najszerszą pętlę histerezy pośród badanych materiałów posiada ferryt, zatem jest on magnetykiem twardym. Jego przewodnictwo zwiększa się wraz z przyrostem temperatury. Po wyłączeniu zewnętrznego pola magnetycznego ferryt pozostaje przez pewien czas namagnesowany.

7. Dla blachy krzemowej zwiększając prąd Isk pętla przechodzi od soczewkowego kształtu do podobnego z rysunku 2. Przemieszczenie punktu Bmax, Hmax następuje po linii krzywej.

8. Za pomocą pętli histerezy można dobrać odpowiednie materiały do potrzeb, np. dla transformatorów dobiera się materiały miękkie (szybkie przemagnesowywanie), a do zapisu danych (kasety magnetofonowe, dyski twarde) dobiera się materiały półtwarde, magnetyki twarde to magnesy trwałe o bardzo szerokiej pętli histerezy i koercji sięgającej nawet 10MA/m

---