Sprawozdanie nr 7

Logika układów cyfrowych

Prow. A. Sterna

Zadanie 1

Zaprojektować automat przy zastosowaniu języka wyrażeń regularnych

Z2(Z1Z1Z2 + Z1Z2) * Z2

1. Przeprowadzono analizę wyrażenia:

| Z2 | ( | Z1 | Z1 | Z2 | + | Z1 | Z2 | ) * Z2 |

0 1 2 2 3 4 2 3 4 5

2. Stworzono tablicę przejść:

WY	Y0	Y0	Y0	Y0	Y0	Y1
WE	0	1	2	3	4	5
Z1	*	2	3	*	*	*
Z2	1	*	*	4	5	*

WE	0	1	2	3	4	5
Z1	*	2	3	6	5	6
Z2	1	6	6	4	6	4

WE	0	1	2	3	4	5
Z1	Q0	Q4	Q3	Q3	Q5	Q3
Z2	Q1	Q2	Q3	Q3	Q1	Q1

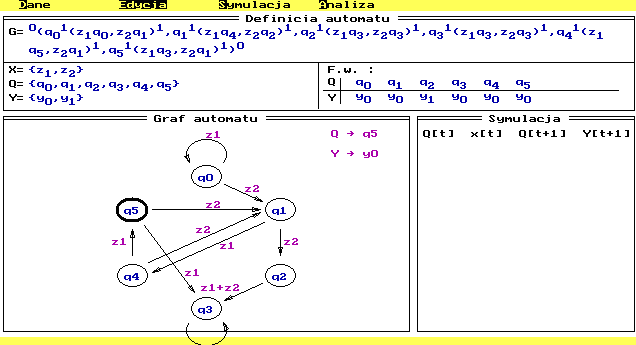
3. Graf zaprojektowanego automatu wygląda następująco:

(docelowo ze stanu q0 po z1 powinno nastąpić przejście do stanu q3, jednak w zaprojektowanym automacie następuje pętla w q0)

4. Tablice prawdy dla automatu:

	Q2	Q1	Q0
q0	0	0	0
q1	0	0	1
q2	0	1	0
q3	0	1	1
q4	1	0	0
q5	1	0	1

Przy przejściach JK następuje:

00 0 -

01 1 -

10 - 1

11 - 0

Mamy do uwzględnienia Q1, Q2, Q3 oraz Z, który wg alfabetu wejściowego przyjmuje wartości 0 lub 1 (z1 i z2)

Q2	Q1	Q0	Z	Q2	Q1	Q0	J2	K2	J1	K1	J0	K0
0	0	0	0	0	0	0	0	-	0	-	0	-
0	0	1	0	1	0	0	1	-	0	-	-	1
0	1	0	0	0	1	1	0	-	-	0	1	-
0	1	1	0	0	1	1	0	-	-	0	-	0
1	0	0	0	1	0	1	-	0	0	-	1	-
1	0	1	0	0	1	1	-	1	1	-	-	0
0	0	0	1	0	0	1	0	-	0	-	1	-
0	0	1	1	0	1	0	0	-	1	-	-	1
0	1	0	1	0	1	1	0	-	-	0	1	-
0	1	1	1	0	1	1	0	-	-	0	-	0
1	0	0	1	0	0	1	-	1	0	-	1	-
1	0	1	1	0	0	1	-	1	0	-	-	0

5. Siatki Karnaugh'a dla każdego J i K

Q0Q1 Q2 Z	00	01	11	10
00	0	0	0	1
01	0	0	0	0
11	-	-	-	-
10	-	-	-	-
Q0Q1 Q2 Z	00	01	11	10
00	-	-	-	-
01	-	-	-	-
11	1	-	-	1
10	0	-	-	1

Q0Q1 Q2 Z	00	01	11	10
00	0	-	-	0
01	0	-	-	1
11	0	-	-	0
10	0	-	-	1
Q0Q1 Q2 Z	00	01	11	10
00		0	0
01		0	0
11
10

Q0Q1 Q2 Z	00	01	11	10
00	-	-	0	1
01	-	-	0	1
11	-	-	-	0
10	-	-	-	0

Q0Q1 Q2 Z	00	01	11	10
00	0	1	-	-
01	1	1	-	-
11	1	-	-	-
10	1	-	-	-

6. Równania do siatek :

K₁ = 1

K₂ = Z + Q₀

7. Przekształcenia równań:

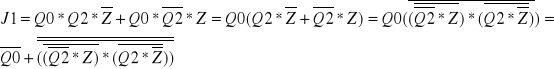
K1= 1

8. Rysowanie schematu:

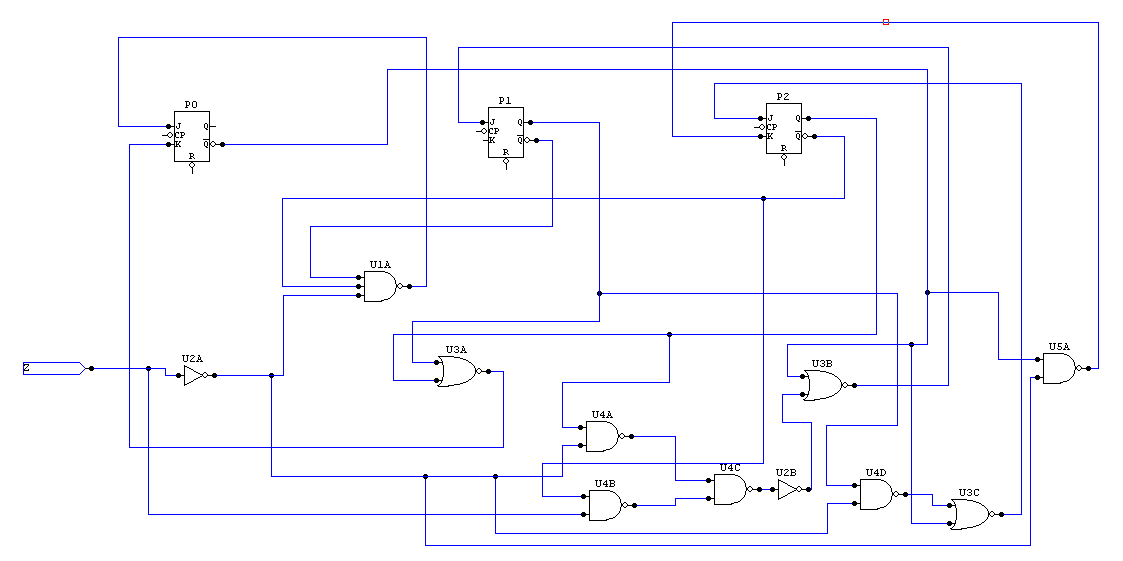
9. Wnioski:

Układ podłączony poprawnie.

K0

J1

K2

J2

K1

J0