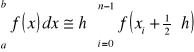
1.Całkowanie funkcji metodą prostokątów.

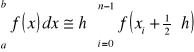
2.Całkowanie funkcji metodą trapezów.

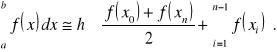
3.Rozwiązanie równania nieliniowego metodą połowicznego podziału

[a_i, b_i]; f(a_i)⋅ f(b_i)<0

4.Rozwiązanie równania nieliniowego metodą Newtona (metoda stycznych)

5.Interpolacja funkcji za pomocą wielomianu Lagrange'a

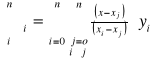
6.Interpolacja funkcji za pomocą funkcji sklejanej z wielomianów stopnia pierwszego

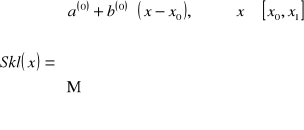
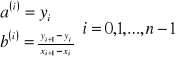
7.Aproksymacja funkcji, za pomocą funkcji potęgowej.

8.Aproksymacja funkcji, za pomocą funkcji wykładniczej

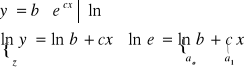
9.Rozwiązanie zagadnienia początkowego metodą Eulera.

lub

w₁ = α +h ⋅ f(x_o, w_o)

w'(x₁)=f (x₁,w₁)

w₂ = w₁ +h ⋅ f(x_1,w₁)

10. Rozwiązanie zagadnienia początkowego metodą Rungego - Kutty II-go rzędu.

w1 = w0 + h* f (x0 + ½*h , w0 + ½ * h * f (x0, w0))

w _{i +1} = w _i + h * f (x _i + ½*h, w _i + ½ * h * f (x _i , w _i)) i = 0,1, ... , n-1

k1 = * h * f (x _i , w _i)

k2 = h * f (x _i + ½*h, w _i + ½ * h * f (x _i , w _i))

11. Rozwiązywanie układu równań liniowych metodą Gaussa

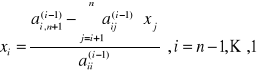
12. Rozwiązywanie układu równań liniowych metodą Thomasa.

13. Rozwiązanie zagadnienia początkowo - brzegowego, z równaniem różniczkowym typu parabolicznego, przy użyciu schematu 4 - punktowego niejawnego.

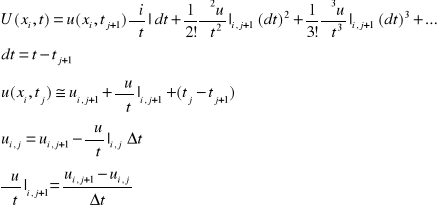
15. Rozwiązanie zagadnienia początkowo - brzegowego, z równaniem różniczkowym typu parabolicznego, przy użyciu schematu 4 - punktowego jawnego.

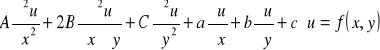
1]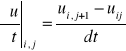

[2]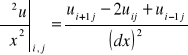

do rów. [0] podstawiamy równ.[1] i [2] i otrzymujemy

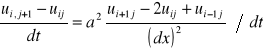
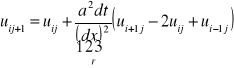
Ostateczna postać RR przy sch. jawnym.