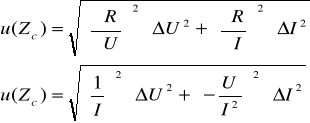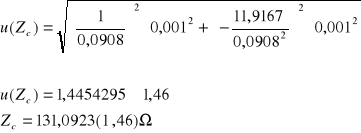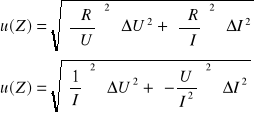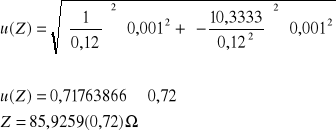I = l0 sin![]()
t ![]()
= ![]()
0 sin![]()
t
U = U0 sin![]()
t
ĆWICZENIA LABORATORYJNE Z FIZYKI
S P R A W O Z D A N I E
Temat: Wpływ oporu, indukcji i pojemności na natężenie prądu zmiennego.
para nr 8, ćwiczenie nr 40
Towaroznawstwo
Grupa 14
Prądem zmiennym (przemiennym) nazywa się taki prąd, którego natężenie I oraz siła elektromotoryczna E lub napięcie U są okresowymi funkcjami czasu.
I = l0 sin![]()
t ![]()
= ![]()
0 sin![]()
t
U = U0 sin![]()
t
gdzie:
![]()
= 2![]()
,
![]()
- częstotliwość prądu (dla prądu sieciowego ![]()
= 50 Hz).
Przyrządy używane w tym ćwiczeniu, jak - amperomierz i woltomierz nie rejestrują okresowych zmian natężenia i napięcia w czasie, O natomiast mierzą natężenie i napięcie skuteczne. W dowolnym obwodzie prądu zmiennego można wyróżnić trzy podstawowe grupy elementów o charakterystycznych parametrach elektrycznych są to:
oporność - elementy obwodu, których charakterystycznym parametrem elektrycznym jest rezystancja R, czyli tzw. opór omowy (rezystory, zwojnice, przewody),
indukcyjność - elementy obwodu o współczynniku indukcji własnej L, w których zachodzi zjawisko indukcji elektromagnetycznej (zwojnice, cewki),
pojemność - kondensatory i inne elementy o pojemności C.
Jako modelowy obwód prądu zmiennego można traktować obwód składający się z oporu, indukcyjności i pojemności, połączonych szeregowo, czyli obwód RLC.
Rozpatrzymy wpływ poszczególnych elementów obwodu RLC na przepływ prądu zmiennego.
a. Wpływ rezystancji na przepływ prądu stałego i zmiennego
Związek między napięciem U lub siłą elektromotoryczną ![]()
a natężeniem prądu I wyraża prawo Ohma:
![]()
gdzie:
R - rezystancja.
Prawo Ohma opisuje przepływ prądu zarówno ze źródła prądu stałego, jak i prądu zmiennego.
Podczas przepływu prądu przez rezystor zostaje wykonana praca W. Zgodnie z zasadą zachowania energii układ przekazuje otoczeniu energię w postaci ciepła Q, w ilości równej wykonanej pracy.
Q = W
Ciepło wydzielone w czasie t, oblicza się ze wzoru Joule'a-Lenza:
Q = R I 2 t
W ten sposób część energii źródła prądu zostaje rozproszona na rezystorze w ilości zależnej od oporu omowego R.
Z powyższych rozważań wynika, że rezystancja R w obwodzie zarówno prądu stałego, jak i zmiennego powoduje rozpraszanie energii elektrycznej, a więc wpływa na zmniejszenie natężeni.a prądu I.
W ćwiczeniu aby obliczyć rezystancję R cewki należy połączyć ją ze źródłem prądu stałego. Za pomocą woltomierza i amperomierza zmierzyć napięcie U i natężenie I prądu stałego, a następnie z prawa Ohma wyliczyć rezystancję R.
![]()
b. Wpływ indukcyjności i pojemności na natężenie prądu zmiennego
Prostym modelem symulującym obwody RLC jest obwód, składający się z cewki (solenoidu) o współczynniku indukcji własnej L i kondensatora o pojemności C, zasilany źródłem o sile elektromotorycznej ![]()
= ![]()
0 sin![]()
t. Cewka indukcyjna wykazuje także opór omowy R, ponieważ włączona do obwodu prądu stałego zachowuje się jak rezystor. Stąd wniosek, że obwód zamknięty składający się z cewki i kondensatora jest obwodem RLC. Istotną rolę w takim obwodzie odgrywa zjawisko indukcji elektromagnetycznej. Zgodnie z podstawowymi prawami elektromagnetyzmu (prawa Maxwell'a), zjawisko indukcji elektromagnetycznej polega na powstawaniu w przewodniku siły elektromotorycznej c wywołanej przez zmienne w czasie pole magnetyczne. Wartość indukowanej siły elektromotorycznej c w obwodzie jest proporcjonalna do szybkości zmian strumienia pola magnetycznego:
![]()
gdzie:
![]()
- strumień pola magnetycznego.
Wzór ten jest ogólnym opisem matematycznym zjawiska indukcji elektromagnetycznej. Pozwala wyjaśnić zjawisko i obliczyć indukowaną w obwodzie siłę elektromagnetyczną w różnych przypadkach. Za pomocą tego wzoru można również opisać zjawisko indukcji elektromagnetycznej wzajemnej i własnej oraz wyjaśnić zasadę działania prądnicy i innych urządzeń, w których zachodzi zjawisko indukcji elektromagnetycznej.
W tym ćwiczeniu zjawisko indukcji elektromagnetycznej własnej występuje w cewce (zwojnicy), gdy w obwodzie RLC płynie prąd zmienny. Strumień ![]()
pola magnetycznego w zwojnicy jest proporcjonalny do natężenia prądu zmiennego I:
![]()
czyli
![]()
gdzie:
L - współczynnik indukcji własnej.
Siła elektromotoryczna indukcji własnej jest więc proporcjonalna do szybkości zmian w czasie natężenia prądu płynącego przez zwojnicę. Współczynnik L jest charakterystyczny dla danej zwojnicy i zależy od jej parametrów geometrycznych. Zależność ta wyraża się wzorem:
![]()
gdzie:
![]()
- względna przenikalność magnetyczna ośrodka,
![]()
0 - przenikalność magnetyczna próżni,
n - liczba zwojów,
l - długość cewki,
r - promień poprzecznego przekroju cewki.
Należy wziąć pod uwagę fakt, że wartość oporu omowego R przewodnika zależy od parametrów charakterystycznych dla danego przewodnika: jego długości, pola przekroju poprzecznego i oporu właściwego. Wartość oporu indukcyjnego RL i oporu pojemnościowego Re (tzw. oporów biernych), oprócz parametrów charakteryzujących cewkę (L) i kondensator (C), zależy również od częstotliwości w siły elektromotorycznej wymuszającej przepływ prądu zmiennego w obwodzie.
Z przedstawionej wyżej dyskusji przepływu prądu zmiennego w obwodzie RLC wynika, że włączenie w obwód elementów o indukcyjności L i pojemności C powoduje zmniejszenie natężenia prądu zmiennego.
Jak wynika ze wzoru:
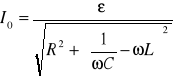
amplituda prądu w obwodzie RLC jest mniejsza niż amplituda prądu zmiennego płynącego w obwodzie, w którym jest tylko opór R. Jest to spowodowane powstawaniem pola elektrycznego w kondensatorze i pola magnetycznego w cewce. Energia źródła prądu, dzięki której są przemieszczane nośniki prądu w obwodzie, jest pomniejszona o straty energii przy powstawaniu pola elektrycznego w kondensatorze i pola magnetycznego w cewce indukcyjnej.
Z tego wyrażenia wynika również, że natężenie prądu w obwodzie w decydujący sposób zależy od różnicy między oporem indukcyjnym i oporem pojemnościowym. Jeżeli
RL > RC, to obwód ma charakter indukcyjny. Występuje wtedy przewaga kumulacji energii źródła prądu w polu magnetycznym cewki. Gdy RL < RC, wówczas obwód ma charakter pojemnościowy, tzn., że energia źródła prądu gromadzi się głównie w polu elektrycznym kondensatora. Szczególny przypadek zachodzi wtedy, gdy wymuszająca przepływ prądu siła elektyromotoryczna jest w rezonansie z obwodem RLC, czyli amplituda 10 natężenia prądu osiąga wartość maksymalną. Jak wynika z powyższego wzoru ma to miejsce wtedy, gdy wyrażenie w nawiasie, pod pierwiastkiem, równa się zeru, czyli:
Rc = RL
![]()
stąd
![]()
gdzie:
![]()
- częstotliwość rezonansowa,
![]()
- częstotliwość drgań własnych obwodu.
Zjawisko rezonansu dla natężenia prądu zachodzi więc wtedy, gdy częstotliwość siły elektromotorycznej, powodującej przepływ prądu, równa się częstotliwości drgań własnych obwodu RLC. Są to najkorzystniejsze warunki przepływu prądu ze względu na wartość natężenia prądu. Możemy je uzyskać, odpowiednio zmieniając parametry L i C obwodu bądź dobierając siłę elektromotoryczną ![]()
o odpowiedniej częstotliwości ![]()
Zgodnie z równaniem ![]()
zawada obwodu wyrazi się wzorem:
![]()
Jest to tzw. zawada indukcyjna. Wystarczy zmierzyć napięcie skuteczne U na cewce oraz natężenie skuteczne I prądu płynącego w obwodzie, aby obliczyć wartość zawady indukcyjnej ze wzoru:
![]()
Tak zmierzoną wartość zawady indukcyjnej można wykorzystać do wyznaczania współczynnika indukcji własnej L cewki. Po przekształceniu wzoru (5.90) otrzymuje się:
![]()
L=![]()
Można przyjąć, że opór indukcyjny RL obwodu jest równy zeru. Wzór na zawadę takiego obwodu, zgodnie z równaniem, przyjmie postać:
![]()
- zawada pojemnościowa
gdzie:
Rl - opór przewodników łączących elementy obwodu.
W tym ćwiczeniu oraz w wielu innych przypadkach, opór RI jest znacznie mniejszy od oporu pojemnościowego Re, stąd można zapisać:
Zc=Rc
Zawadę pojemnościową wyznacza się ze wzoru:
![]()
gdzie:
U oraz I to napięcie i natężenie skuteczne prądu zmiennego w obwodzie z kondensatorem.
Zawada obwodu RLC. Aby wyznaczyć zawadę obwodu RLC, należy elementy obwodu połączyć ze źródłem prądu zmiennego. Zmierzyć napięcie skuteczne U i natężenie skuteczne I prądu zmiennego, płynącego w tym obwodzie oraz obliczyć zawadę ze wzoru ![]()
OBLICZENIA I POMIARY:
Wpływ oporu, indukcji i pojemności na natężenie prądu zmiennego.
|
Pomiary |
U |
I |
R |
ZL |
RL |
L |
ZC = RC |
Z |
|
|
V |
A |
Ω |
Ω |
Ω |
H |
Ω |
Ω |
Układ I (prąd stały) |
1 2 3 |
0,325 0,5 0,975 |
0,024 0,035 0,065 |
13,5417 14,2857 15 |
|
57,3036 |
0,1318 - ze wzoru (1) 0,0241 - ze wzoru (2) |
|
|
Układ II (prąd zmienny) |
1 2 3 |
5,75 8,25 12,5 |
0,09 0,14 0,23 |
|
63,8888 58,9286 54,3478 |
|
|
|
|
Układ III (prąd zmienny) |
1 2 3 |
10,5 11,75 13,5 |
0,08 0,0925 0,1 |
|
|
|
|
131,25 127,027 135 |
|
Układ IV (prąd zmienny) |
1 2 3 |
7,75 10 13,25 |
0,09 0,12 0,15 |
|
|
|
|
|
86,1111 83,3333 88,3333 |
średnie |
|
14,2758 |
59,0551 |
|
131,0923 |
85,9259 |
|||
zawada ze wzoru (2) |
75,1569 |
||||||||
Henr: ![]()
Opór omowy cewki: ![]()
Wartość zwady indukcyjnej: ![]()
Opór indukcyjny cewki: ![]()
Współczynnik samoindukcji (1): ![]()
Współczynnik samoindukcji (2): ![]()
Zawada pojemnościowa: ![]()
Zawada (1): ![]()
Zawada (2): ![]()
n = 2050
r = 0,026 m
l = 0,085 m
![]()
= 2![]()
![]()
= 50 Hz
Obliczenie wartości niepewności:
ΔU = 0,001 V
ΔI = 0,001 A
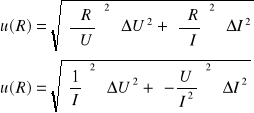

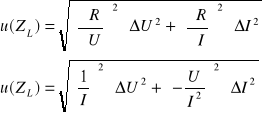
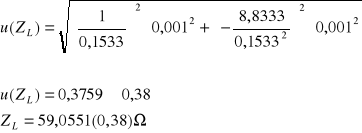
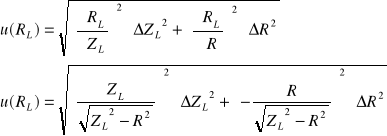
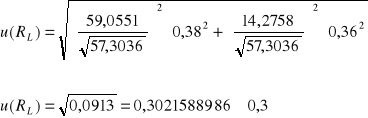
![]()
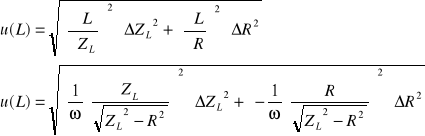
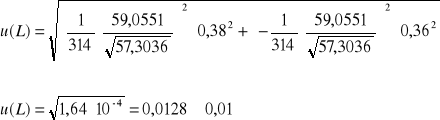
![]()