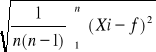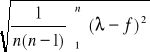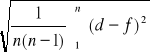Informatyka I rok |
Rudlicki Krzysztof |
Data pomiarów : 10.03.2008 |
|
Numer ćwiczenia: 17 |
|
Ocena : |
|
Uwagi |
|||
Wiadomości wstępne- wprowadzenie do teorii lasera
Zasada działania lasera wynika wprost z rozwinięcia skrótu LASER - Light Amplification by Stimulated Emission of Radiation - wzmocnienie światła przez wymuszona emisję promieniowania. Fenomen lasera nie jest zawarty w sposobie działania czy konstrukcji, lecz w rodzaju światła jakie urządzenie to emituje. Jest to bardzo skupiona wiązka światła monochromatycznego, czyli o jednej, ściśle określonej barwie (długości fali). Cechy te dają laserowi niezwykłą przewagę nad innymi źródłami światła.
W laserze wykorzystuje się efekty wzajemnego oddziaływania promieniowania elektromagnetycznego z materią - tzw. ośrodkiem aktywnym, którym może być ciało stałe, ciecz lub gaz. Zasadniczymi częściami lasera są: ośrodek czynny, rezonator optyczny, układ pompujący. Układ pompujący dostarcza energię do ośrodka czynnego, w ośrodku czynnym w odpowiednich warunkach zachodzi akcja laserowa, czyli kwantowe wzmacnianie (powielanie) fotonów, a układ optyczny umożliwia wybranie odpowiednich fotonów.
Lasery dzielą się ze względu na materiał aktywny i sposób pobudzania. Stan skupienia ośrodków wzmacniających jest najbardziej ogólnym i najczęściej stosowanym kryterium podziału laserów. Materiał aktywny pozwala wyróżnić lasery: gazowe, cieczowe, na ciele stałym i półprzewodnikowe.
Zastosowania lasera:
Wojskowe: z początku główna idea (do której następuje teraz powrót): lasery dużej mocy niszczące obiekty powietrzne i naziemne, z czasem jednak najbardziej powszechne zastosowanie w urządzeniach „oznaczających” cele, które są następnie niszczone przez rakiety naprowadzane wiązką światła.
„Nad poligonem White Sands w Nowym Meksyku dokonano pierwszego przechwycenia i zestrzelenia laserem pocisku lecącego z prędkością naddźwiękową. Naświetlenie trwało kilka sekund, po czym cel został rozerwany na części. (…)”
Minister Obrony Donald Rumsfeld przyznał temu programowi najwyższy priorytet.
Medycyna:
Chirurgia - rozcinanie tkanek - lepsze niż skalpel, gdyż skalpel się tępi i trzeba go sterylizować, poza tym tkanki cięte laserem zasklepiają się na skutek działającej temperatury.
Okulistyka - przyklejanie uszkodzonej siatkówki do dna oka,
Stomatologia - bezbolesne „wiercenie” zęba - chora tkanka odparowywuje
Dermatologia i chirurgia plastyczna - usuwanie zmian naczyniowych, brodawek, przebarwień skóry… a nawet diagnostyka nowotworów!
Zastosowania techniczne:
Spawanie materiałów:
Precyzja, czystość, automatyzacja, bez dodatkowego spoiwa, wysoka jakość spawu
możliwość spawu w gazach ochronnych: hel, argon, dwutlenek węgla, azot.
Cięcie materiałów:
wysoka jakość i wysoka prędkość procesu, gładkie krawędzie, mała strata materiału, łatwa automatyzacja procesu
materiały wszelkiego rodzaju: stal, tytan, pleksi, drewno, szkło, papier, tekstylia
różnorodność technologiczna procesu (odparowanie, wypalanie, topienie + wydmuch, poprzez pęknięcia termiczne itp.)
przemysł maszynowy, włókienniczy, samochodowy.
A także:
Skanowanie kodu paskowego w sklepach, płyty (CD, DVD, H-DVD, Blue-Ray), geodezja (głównie pomiary odległości, wyznaczanie linii prostych), hologramy, oraz w poligrafii do stworzenia cyfrowych kserokopiarek.
2. Tabele pomiarowe i sposoby liczenia
Stala d
|
Odleglosc l
|
Odleglosc a
|
Dl . fali
|
Rząd widma n |
Srednica D
|
SIATKA DYFRAKCYJNA |
|||||
5000 |
665
|
180 |
670.5787 |
1 |
|
|
|
370 |
670,0436125 |
2 |
|
|
|
584 |
670,0772868 |
3 |
|
SZCZELINA |
|||||
|
2350 |
26 |
680 |
1 |
0,1843846154 |
|
|
44 |
|
2 |
0,1815909091 |
|
|
62 |
|
3 |
0,1804193548 |
|
|
78 |
|
4 |
0,1843846154 |
|
|
114 |
|
6 |
0,1822280702 |
DRUCIK ( 0,1mm) |
|||||
|
2330 |
72 |
680 |
1 |
0,0660166666 |
|
|
120 |
|
2 |
0,0660166666 |
|
|
172 |
|
3 |
0,0644813935 |
|
|
324 |
|
6 |
0,0635716049 |
Wyznaczenie długości fali :
gdzie
-długość fali;
-odległość między maksimami;
n- rząd widm;
l-odległość lasera od ekranu
Wyznaczenie średnicy badanego drucika z zależności :
gdzie
-odległość środka plamki ciemnej n rzędu od środka wiązki nie ugiętej
n-rząd widma
D-średnica drutu
l - odlieglość drucika od ekranu
Wyznaczenie szerokości szczeliny z zależności :
gdzie :
S-szerokość szczeliny
- długość fali
l - odlieglość szczeliny od ekranu
-odległość środka plamki ciemnej n rzędu od środka wiązki nie ugiętej
n- rząd widma
Wyznaczanie błędów pomiarowych
Błąd pomiarowy szerokości szczeliny
Szer.Szczeliny(Xi) [mm] |
Srednia (f) [mm] |
[mm] |
U(f)= |
0.184384 |
0.182601 |
0.000003179089 |
0.000783312 |
0.181590 |
|
0.000001022121 |
|
0.180419 |
|
0.000004761124 |
|
0.184384 |
|
0.000003179089 |
|
0.182228 |
|
0.000000139129 |
|
Suma |
0.000012271552 |
|
|
Przyjmując poziom ufności α = 0.7
U(f)* t (α *n ) = 0.000783312 * 1.2= 0.000939975 mm
f(0.182228 ± 0.000939975 ) mm
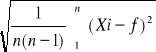
gdzie:
n- Liczba pomiarów
Xi- poszczególne pomiary
f- średnia arytmetyczna pomiarów
Błąd pomiarowy długości fali
Długość fali (λ) [mm] |
Srednia (f) [mm] |
(λ-f) [mm] |
U(f)= |
670.578 |
670.233
|
0.119025 |
0.171629931
|
670.043 |
|
0.0361 |
|
670.077 |
|
0.021616 |
|
Suma |
0.176741 |
|
|
Przyjmując poziom ufności α= 0.7
U(f)* t (α *n ) = 0.22311891 mm
f = (670.233± 0.22911891 ) mm
Błąd pomiarowy średnicy drucika
Szerokość drutu (d) [mm] |
Srednia (f) [mm] |
(d-f) [mm] |
U(f)= |
0.066016 |
0.065021 |
0.000995 |
0.018211717 |
0.066016 |
|
0.000995 |
|
0.064481 |
|
0.000540 |
|
0.063571 |
|
0.001450 |
|
Suma |
0.003980 |
|
|
Przyjmując poziom ufności α=0.7
U(f)* t (α *n ) = 0.023675233 mm
f(0.065021 ± 0.023675233 ) mm
Wnioski
- Wyznaczona długości fali za pomocą siatki dyfrakcyjnej odbiega od rzeczywistej wartości
długości fali. Różnica ta spowodowana jest faktem, że pomiary te były dokonywane za pomocą
liniału o dokładności 1mm.
- Lasery są obecnie bardzo szeroko wykorzystywane we wszystkich dziedzinach techniki i nauki. Za pomocą laserów można z wielką dokładnością dokonywać różnego rodzaju pomiarów. Na błędy pomiarowe w ćwiczeniu wpływ miało kilka czynników : znaczny błąd pomiaru odległości, oraz niedokładność pomiarów kolejnych maksimów.
- odległość między widmami tego samego rzędu szczeliny jest zauważalnie mniejsza od odległości widm Siatki dyfrakcyjnej
