1. Cel ćwiczenia

Celem pomiarów jest wyznaczenie prędkości pocisku za pomocą wahadła balistycznego skrętnego.

2. Wykorzystane zależności

Korzystając z tego, iż zderzenie wahadła (jego miseczki wypełnione są plastelina) z pociskiem jest całkowicie niesprężyste (pocisk wbija się w plastelinę) można napisać równanie zachowania momentu pędu

(1)

gdzie: m - masa pocisku,

v - jego prędkość,

r - odległość wbitego pocisku od osi obrotu,

ω - prędkość kątowa wahadła,

I₁ - moment bezwładności wahadła

Odkształcenie jakiemu podlega drut wahadła, ma charakter sprężysty, zatem zgodnie z prawem Hooke'a moment sił sprężystości M jest proporcjonalny do kąta skręcenia wahadła φ:

(2)

gdzie
- sztywność skrętna drutu,

l - długość drutu

d - średnica drutu,

G - moduł sprężystości postaciowej (dla stali G=8,5 * 10⁴ MPa)

Maksymalna energia skręcanego drutu jest zatem równa:

(3)

Z zasady zachowania energii mechanicznej wynika, że:

(4)

gdzie φ_max - maksymalny kąt skręcenia wahadła

Z równań (1) i (4) wynika, że:

(5)

Wiedząc, że I₁ >> mr² z (5) otrzymujemy:

(6)

Będziemy uważać także, że czas oddziaływania pocisku na wahadło (czas zderzenia t jest dużo mniejszy od okresu drgań wahadła T

t << T (7)

Równanie ruchu wahadła balistycznego w tych warunkach można zapisać w następującej postaci:

(8)

gdzie: φ - kąt skręcenia od położenia równowagi,

- przyśpieszenie kątowe,

kφ - moment sił sprężystości

Czyli:

(9)

Ogólnie rozwiązanie tego równania ma postać

(10)

gdzie φ_max - amplituda drgań (największe skręcenie),

ω - prędkość kątowa,

α - faza --> [Author:WK] początkowa ruchu (przy odpowiednim doborze chwili pomiaru czasu α=0)

(11)

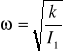
(12)

Zarazem:

(13)

(14)

gdzie T₁ - okres drgań wahadła gdy moment bezwładności wynosi I₁

Aby wyznaczyć z równań wartość współczynnika sztywności k, należy zmienić moment bezwładności wahadła zmieniając odpowiednio położenie ciężarków C na ramionach wahadła.

Wówczas:

(15)

gdzie T₁ -okres drgań, gdy moment bezwładności wynosi I₁

T₂ -okres drgań, gdy moment bezwładności wynosi I₂

Z równań (15) otrzymujemy:

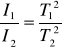
(16)

uwzględniając:

(17)

gdzie
I - różnica momentów bezwładności

Z równań (16) i (17) otrzymujemy:

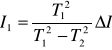
(18)

Korzystając z (6), (14) i (18) uzyskujemy:

(19)

Moment bezwładności I₁ wahadła, gdy ciężarki umieścimy w odległości R₁ od osi obrotu i moment bezwładności I₂, gdy ciężarki umieścimy w odległości R₂ są następujące:

(20)

gdzie I₀ - moment bezwładności wahadła bez ciężarków,

M - masa ciężarka.

Gdy weźmiemy tak, aby R₁>R₂ wtedy z (20) uzyskujemy:

(21)

ostatecznie z (19) i (21) otrzymujemy:

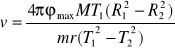
(22)

gdzie v - szukana prędkość pocisku,

φ_max - maksymalny kąt wychylenia wahadła po zderzeniu z pociskiem,

M - masa ciężarka,

m - masa pocisku,

r - odległość osi obrotu wahadła od środka pocisku wbitego w plastelinę,

R₁ - odległość osi obrotu od środka ciężarka, gdy jest on najbliżej miseczki z plasteliną,

R₂ - odległość osi obrotu od środka ciężarka, gdy jest on najbliżej osi obrotu (czyli R₁>R₂),

T₁ - okres drgań dla R_1,

T₂ - okres drgań dla R_2.

3. Wyniki pomiarów.

Lp.	R2 = min			R1 = max
		φmax	10T2	T2	φmax	10T1	T1
1	48	32,905	3,29	24	56,822	5,682
2	47	32,837	3,283	25	56,832	5,683
3	40	32,832	3,283	24	56,825	5,682
4	46	32,854	3,285	24	56,824	5,682
5	47	32,841	3,284	25	56,836	5,683
6	42	32,835	3,283	24	56,829	5,682
7	46	32,835	3,283	24	56,834	5,683
8	45	32,842	3,284	24	56,830	5,683
9	44	32,834	3,283	24	56,828	5,682
10	45	32,837	3,283	25	56,829	5,682

Lp.	m [kg]	R2 [m]	R1 [m]	r [m]	v [m/s]
1	0,001	0,02	0,09	0,127	3,4132

4. Obliczony błąd bezwzględny prędkości dla M = 4dg błąd
   ­0,5dg i m = 1g błąd
   0,5g
   

5. Ocena wpływu na wynik końcowy przyjętych założeń:

1. I­₁ >> mr²

Stosując to przybliżenie możemy uprościć równanie (5) bez strat dla dokładności pomiarów, gdyż moment bezwładności pocisku jest znacznie mniejszy od momentu bezwładności wahadła balistycznego. Gdyby momenty te były równe lub moment bezwładności pocisku był by większy to równanie (6) było by nieprawdziwe gdyż prędkość rzeczywista była by znacznie większa od wyliczonej.

2. t << T

Czas zderzenia pocisku z wahadłem jest równy
. Jak widać czas ten jest znacznie mniejszy od okresu drgań wahadła, co pozwala znacznie uprościć równanie (8). Gdyby jednak czas zderzenia był porównywalny z okresem drgań wahadła wtedy należało by przyjąć, że na wahadło działa zmienna siła w czasie wywołana ruchem pocisku co znacznie by skomplikowało równanie (8).

7

5

---