Różniczka funkcji wektorowej ![]()
ma następującą postać: ![]()
I forma kwadratowa powierzchni
Różniczka funkcji wektorowej ![]()
ma następującą postać: ![]()
Element łuku na powierzchni opisanej równaniem ![]()
ma postać:
ds2 dr|2 Edu2 2Fdudv Gdv2
![]()
![]()
Elementarny łuk na powierzchni kuli
Na powierzchni kuli opisanej równaniem ![]()
![]()
![]()
obliczamy współczynniki I formy kwadratowej
E = R2, F = 0, G = R2cos2φ, H = R2|cosφ|
Elementarny łuk na powierzchni kuli ma postać:
ds2 = R2d φ2 + R2cos2 φ dλ2
Elementarny łuk na powierzchni elipsoidy
Na powierzchni elipsoidy opisanej równaniem:
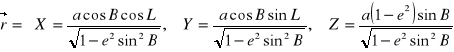
![]()
obliczamy współczynniki I formy kwadratowej:
E = M2, F = 0, G = N2cos2B, H = MN|cos|B|
Elementarny łuk na powierzchni elipsoidy ma postać:
ds2 = M2dB2 + N2cos2BdL2
Skala
Związek pomiędzy skalą poszczególną μp, skalą główną μ0 i elementarną skalą zniekształceń odwzorowawczych μ.
![]()
μ0 - skala główna odwzorowania, wyraża stosunek zmniejszenia wymiarów liniowych, pomniejszenie powierzchni oryginały (odwzorowanie przez podobieństwo), skala główna jest liczbą rzeczywistą przedstawioną w postaci μ0 = 1/M
Elementarne skale zniekształceń długości
Elementarne skale zniekształceń długości jest to stosunek odpowiadających sobie elementarnych łuków na powierzchni obrazu i na powierzchni oryginału:
μ = ds'/ds.,
gdzie ds - element łuku na powierzchni oryginału,
ds' - element łuku na powierzchni obrazu.
Elementarna skala zniekształceń długości jest funkcją trzech zmiennych: współrzędnych (u,v) wyznaczających położenie punktu na powierzchni oryginału oraz kąta kierunkowego A elementu ds na powierzchni oryginału μ = μ (u,v,A)
Elementarna skala zniekształceń długości
Elementarną skalą zniekształceń długości można przedstawić w postaci wektorowej 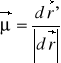
gdzie ![]()
jest różniczką funkcji r = r(u,v) opisującej powierzchnię oryginału w odwzorowaniu kartograficznym oraz ![]()
jest różniczką funkcji r' = r'(u,v) opisującej powierzchnię obrazu w odwzorowaniu kartograficznym.
Elementarne zniekształcenie długości jest to odchylenie elementarnej skali zniekształceń długości od jedności:
![]()
Elementarna skala zniekształceń długości w kierunku linii parametrycznych
Podstawiając do wzoru na skalę ![]()
elementarne łuki na powierzchni oryginału i powierzchni obrazu
![]()
![]()
otrzymujemy wzór na skalę w postaci:
![]()
Obliczając skalę w kierunku południka v = const podstawiamy dv = 0 otrzymujemy ![]()
Obliczając skalę w kierunku równoleżnika u = const podstawiamy du = 0 otrzymujemy ![]()
Skale w kierunku linii parametrycznych noszą nazwę skal parametrycznych.
Dla powierzchni kuli skale parametryczne mają postać: ![]()
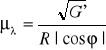
Dla elipsoidy skale parametryczne mają postać ![]()
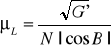
Elementarna skala zniekształceń długości jako funkcji kąta kierunkowego
Elementarną skalę zniekształceń długości ma postać 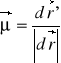
Różniczki ![]()
oraz ![]()
funkcji r = r(u,v) opisującej powierzchnię oryginału oraz funkcji r' = r'(u,v) opisującej powierzchnię obrazu można przedstawić w postaci:
![]()
![]()
Tangens kąta kierunkowego A ma postać ![]()
stąd wyznaczamy ![]()
Zastosowanie powyższego wzoru prowadzi do następujących postaci różniczek:
![]()
![]()
stąd wyznaczamy moduł ![]()
Uwzględniając powyższe rozważania otrzymujemy następującą postać elementarnej skali długości ![]()
gdzie 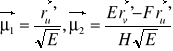
Jeżeli na powierzchni oryginału mamy parametryzację ortogonalną (F=0) wektory μ1 oraz μ2 przyjmą postać 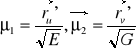
są to wówczas skale parametryczne ![]()
Kwadrat elementarnej skali zniekształceń długości można przedstawić w postaci ![]()
gdzie ![]()
W przypadku parametryzacji ortogonalnej na powierzchni obrazu (F=0) otrzymujemy
![]()