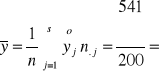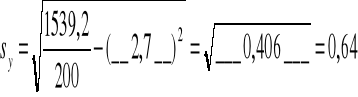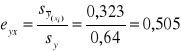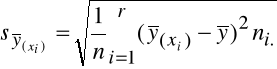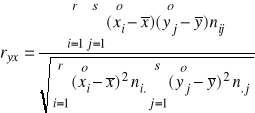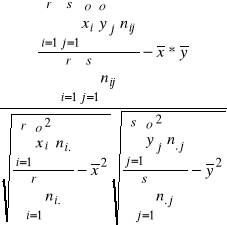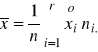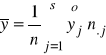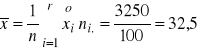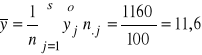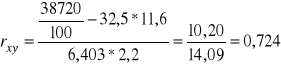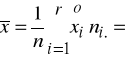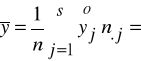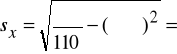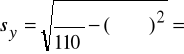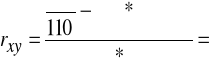Przykład 1 - stosunek korelacji
W celu oszacowania siły związku między wykształceniem pracowników pewnej firmy a ich zarobkami miesięcznymi poddano badaniu 200 pracowników. Wyniki przedstawia tablica. Czy istnieje związek między badanymi cechami ?
Wykształcenie |
Zarobek miesięczny w tys. zł. |
||
|
1,4-2,0 |
2,0-3,0 |
3,0-4,0 |
podstawowe |
10 |
20 |
5 |
zas. zawodowe |
10 |
25 |
5 |
średnie |
5 |
35 |
15 |
wyższe |
5 |
25 |
40 |
Obliczenia przeprowadzimy w tablicy:
Wykształcenie |
Zarobek miesięczny w tys. zł. (środki przedziałów) |
ni. |
|
|
|
||
|
1,7 |
2,5 |
3,5 |
|
|
|
|
podstawowe |
10 |
20 |
5 |
35 |
|
2,41 |
2,9435 |
zas. zawodowe |
10 |
25 |
5 |
40 |
|
2,42 |
3,136 |
średnie |
5 |
35 |
15 |
55 |
|
2,7 |
0 |
wyższe |
5 |
25 |
40 |
70 |
|
3,16 |
14,812 |
n.j |
30 |
105 |
65 |
200 |
|
x |
20,8916 |
|
17 |
50 |
17,5 |
84,5 |
|
||
|
17 |
62,5 |
17,5 |
97 |
|
||
|
8,5 |
87,5 |
52,5 |
148,5 |
|
||
|
8,5 |
62,5 |
140 |
221 |
|
||
|
51 |
262,5 |
227,5 |
541 |
|
||
|
86,7 |
656,25 |
796,25 |
1539,2 |
|
||
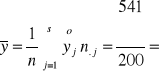
2,7 zł.
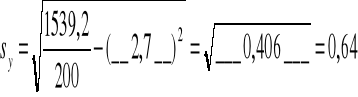
zł.
Stosunek korelacji: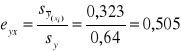 
Odpowiedź:
Przykład - współczynnik korelacji Pearsona dla tablicy korelacyjnej
W wyniku badania zależności między zużyciem surowca i kosztami produkcji uzyskano informacje podane w tablicy.
Zużycie surowca w kg |
Koszt produkcji w tys. zł. |
||||
|
6-8 |
8-10 |
10-12 |
12-14 |
14-16 |
15-24 |
10 |
- |
- |
- |
- |
25-34 |
- |
10 |
20 |
20 |
- |
35-44 |
- |
- |
10 |
20 |
10 |
Na podstawie tych informacji ustalić siłę i kierunek zależności między zużyciem surowca a kosztami produkcji.
Współczynnik korelacji dla tablicy korelacyjnej wyraża się wzorem:
=
gdzie:
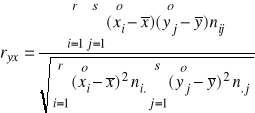
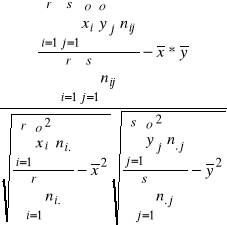
Niezbędne obliczenia przeprowadzimy w tablicy:
Zużycie surowca w kg - X |
środki przedziałów X |
Koszt produkcji w tys. zł. - Y
środki przedziałów |
ni. |
|
|
||||
|
|
6-8 |
8-10 |
10-12 |
12-14 |
14-16 |
|
|
|
|
|
7 |
9 |
11 |
13 |
15 |
|
|
|
15-24 |
19,5 |
10 |
- |
- |
- |
- |
10 |
195 |
3802,5 |
25-34 |
29,5 |
- |
10 |
20 |
20 |
- |
50 |
1475 |
43512,5 |
35-44 |
39,5 |
- |
- |
10 |
20 |
10 |
40 |
1580 |
62410 |
n.j |
10 |
10 |
30 |
40 |
10 |
100 |
3250 |
109725 |
|
|
70 |
90 |
330 |
520 |
150 |
1160 |
x |
x |
|
|
490 |
810 |
3630 |
6760 |
2250 |
13940 |
x |
x |
|
|
1365 |
- |
- |
- |
- |
38720 |
|||
|
- |
2655 |
6490 |
7670 |
- |
|
|||
|
- |
- |
4345 |
10270 |
5925 |
|
|||
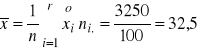
kg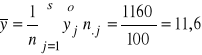 
tys. zł.
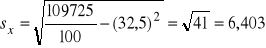
kg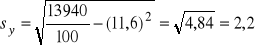 
tys. zł.
Między zużyciem surowca a kosztami produkcji istnieje dodatnia korelacja o dużej sile.
Przykład 2.
W wyniku badania zależności między kosztami zmiennymi produkcji 3 wyrobów i łącznymi kosztami produkcji uzyskano informacje podane w tablicy.
Koszty zmienne w zł |
Koszt produkcji w tys. zł. |
||||
|
6-8 |
8-10 |
10-12 |
12-14 |
14-16 |
10-20 |
10 |
5 |
- |
- |
- |
20-30 |
- |
10 |
20 |
20 |
5 |
30-40 |
- |
- |
10 |
20 |
10 |
Na podstawie tych informacji ustalić siłę i kierunek zależności między kosztami zmiennymi, a kosztami produkcji.
Obliczyć współczynnik korelacji Pearsona dla tablicy korelacyjnej.
Koszty zmienne w zł |
środki przedziałów X |
Koszt produkcji w tys. zł. - Y
środki przedziałów |
ni. |
|
|
||||
|
|
6-8 |
8-10 |
10-12 |
12-14 |
14-16 |
|
|
|
|
|
7 |
9 |
11 |
13 |
15 |
|
|
|
10-20 |
15 |
10 |
5 |
- |
- |
- |
15 |
|
|
20-30 |
25 |
- |
10 |
20 |
20 |
5 |
55 |
|
|
30-40 |
35 |
- |
- |
10 |
20 |
10 |
40 |
|
|
n.j |
10 |
15 |
30 |
40 |
15 |
110 |
|
|
|
|
|
|
|
|
|
|
x |
x |
|
|
|
|
|
|
|
|
x |
x |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|||
Odpowiedź:
