1.Zasada zachowania energii

E=mc² , E₀=m₀c², E_k=E-E₀

E₀-energia spoczynkowa ciała

E-całkowita energia poruszającego się ciała

Często na punkt materialny działa kilka sił. Siła wypadkowa F jest ich sumą geometrii. Praca wykonana przez wypadkową siłę F jest sumą algebraiczną prac wykonanych przez poszczególne siły.

Siła zachowawcza - (występuje w grawitacji, elektromagnetyce, sprężystości) jeżeli siła jest siłą zachowawczą to praca wykonana przez nią podczas przemieszczania się ciałą po drodze zamkniętej jest = 0. Praca nie zależy od drogi

_B → →

E_K^B - E_K^A= -∫ F * dl

^A

F-siła zachowawcza

Zasada zach.energ.mechanicznej

Energia może być przekształcona z jednej formy w inną, ale nie może być wytwarzana ani niszczona. Energia całkowita jest wielkością stałą.

E_K^A + E_P^A =E_K^B + E_P^B

_B → →

∫ F * dl = ΔE_K-ΔE_P+ΔU

^A

u- energia wewn ciałą

Każda praca wykonana na ciele przez czynnik zewnętrzny jest = wzrostowi E_k + wzrost E_P + +wzrost E_WEWN. .

Suma wszystkich rodzajów energii jest stała.

2 Zasada zachowania pędu, zderzenia

xś

----|-------------|--------------|----→

x₁ x₂

m₁ m₂

x_Ś=(m₁x₁+m₂x₂)/(m₁+m₂)

x_Ś=(Εmixi)/(Εmi)

Środek masy układu porusza się tak jakby cała masa byłą w nim skupiona i wszystkie siły zewnętrzne działały na niego

→ →

MV=p {p - pęd}

→ →

Ε F_ZEW = dP/dt

Jeżeli suma sił zewnę. działających na układ jest = 0 wtedy pęd układu pozostaje stały

→ → →

Ε F_ZEW = 0 , dP/dt =0 wtedy p=const

→

p - const - zasada zachowania pędu

Zderzenie niesprężyste - spełniona jest zasada zachowania pędu

M₁ V ₁+ M₂ V₂

Zderzenia sprężyste - są spełnione zasady zachowania pędu i energii kinetycznej

M₁V₁+ M₂V₂ =M₁V₁'+ M₂V₂'

((M₁V₁²)/2+(M₂V₂²)/2 =(M₁V₁'²)/2+(M₂V₂'²)/2

3. Zasada zach.mom.pędu

→ →

M=dl/dt

Moment siły działającej na cząstkę równy jest szybkości zmian wektora momentu pędu cząstki

M_X=dLx/dt , M_Y=dLy/dt , M_Z=dLz/dt

→ → → →

L=L₁+L₂+L₃+...

→ →

Ε M_zew = dL/dt

→ →

L= Iω

Zasada zachowania momentu pędu :

Moment pędu dla układu ciała sztywnego równa się iloczynowi momentu bezwładności i prędkości kątowej ω.

→

Ε M_zew = 0

→ →

dL/dt =0 ⇒ L=const

Prawo zach.mom.pędu dla układu cząstek :

Kiedy wypadkowy moment sił zewnętrznych działających na układ wynosi 0 to całkowity mom.pędu układu pozostaje stały.

→ → →

L=const , Iω = const , ω=const/I

4.Siły bezwładności

Zasada względności - wszystkie układy odniesienia, które poruszają się względem siebie bez przyspieszenia tzn. ruchem jednostajnym po linii prostej są pod względem fizycznym równouprawnione i takie układy nazywamy inercjalnymi

→ →

V₀≠const , a₀≠0

Siła bezwładności (siła uporu bezwładnego )

→ →

F_B= -ma₀

` - ` oznacza że kierunek siły jest zawsze odwrotny do kierunku przyspieszenia

np. Winda

- porusza się w górę

→ → →

F₁=G+ma₀

- porusza się w dół

→ → →

F₁=G-ma₀

- kiedy winda się urwie

→→ →

F=G-mg=0

Siła Coriolisa

Np. wieża i spuszczamy kamień

→ → →

a_C=2V x ω

→ → →

F_C=2mV x ω

Przyspieszenie i siła Coriolisa mają zatem kierunek prostopadły zarówno do osi obrotu, która pokrywa się z kierunkiem ω, oraz prędkości V. Zwrot definiuje reguła śruby prawoskrętnej.

Na podstawie reguły mnożenia wektorowego

→ → → →

v x ω = v x ω

ciała poruszające się na naszej półkuli z pł. na pd. Odchylają się ku zachodowi i odwrotnie na drugiej półkuli. Czyli zawsze odchylają się w prawo względem kierunku ich ruchu. Na półkuli pd. odchylają się przeciwnie.

Np. żłobienie brzegów rzeki praw-pd i lew-pł.

5.Kontrakcja Lorentza, dylatacja czasu

Kontrakcja

Pręt ma największą długość w układzie w którym spoczywa.

Interwał przestrzenny między dwoma punktami A i B

_____________________

r_AB=√(x_A-x_B)²+(y_A-y_B)²+(z_A-z_B)²

_______________________________

S_AB=√c²(t_A-t_B)² - {(x_A-x_B)²+(y_A-y_B)²+(z_A-z_B)²}

Przestrzeń 4-wymiarowa, ktorej interwał czasoprzestrzenny S_AB interpretuje się jako odległości między punktem o współrzędnych x_A,y_A,z_A,t_A i punktem o współrzędnych x_B,y_B,z_B,t_B nazywa się przestrzenią Mińkowskiego .

Dylatacja czasu

Jeżeli z miejsca x₁ w nieruchomym układzie S wysyłane są sygnały o odstępach czasu

Δt=t₂-t₁ to chcemy sprawdzić jaki jest odstęp czasu Δt'=t₂`-t₁' w układzie ruchomym S'.

________ ________

Δt'= t₂`-t₁'=( t₂-t₁)/√(1-(v²/c²)=Δt/√(1-(v²/c²)

1-(v²/c²) < 1

Δt' > Δt

Czyli odstępy czasu Δt w układzie nieruchomym są dla obserwatora ruchomego wydłużone, a więc czas w układzie poruszającym płynie wolniej.

Czas własny jest to czas liczony względem układu odniesienia, w którym ciało znajduje się w spoczynku

6.Ruch drgający prosty wahadła.

Ciało które drga nazywamy oscylatorem. W ruchu drgającym - oscylator harmoniczny

F= - kx - ruch drgający prosty

ma+kx=0

Energia kinetyczna w ruchu drgającym

K=(1/2)mω²Asin²(ωt+ϑ)

ϑ - przesunięcie fazowe

Energia potencjalna w ruchu drgającym

U=(1/2)kA²cos²(ωt+ϑ)

Całkowita energia w ruchu drgającym prostym

E=K+U=(1/2)kA²

Wahadłem matematycznym - nazywamy wyidealizowane ciało o masie punktowej zawieszone na cienkiej nie rozciągalnej nici.

F= -mgsinα , sinα ≈ αn (rad)

F= -mgα

α = x/l

F= -mg(x/l) , F= -kx ⇒ k=(mg)/l

Okres drgań zależy od długości ramienia

T=2π√l/g

7.Ruch drgający tłumiony i wymuszony

Ruch drgający tłumiony - to taki ruch, w którym działająca siła jest siłą oporu.

Równanie ruchu drgającego tłumionego

(d²x)/dt²+2β(dx/dt)+ω₀²x = 0

Logarytmiczny dekrement tłumienia

Λ=ln{(A(t))/(A(t+T))}=β*T

Drgania wymuszone

F=F₀cosΩt

Stwierdzamy:

1.Nie występuje tłumienie drgań, ponieważ doprowadzona z zewnątrz energia równoważy straty energii na pokonanie oporów ruchu.

2.Układ zaczyna drgać z częstotliwością Ω

3.Amplituda drgań zależy od częstotliwości

Równanie ruchu drgającego wymuszonego

(d²x)/dt²+2β(dx/dt)+ω₀²x = βcosΩt

______________

A=B/√(ω₀²-Ω²)²+4β²Ω²

Rezonans - ekstremum amplitudy

dA/dΩ = 0

Wzór na częstotliwość rezonansową

______

Ω_REZ=√ω₀²-2β²

______

A_REZ=B/(2β√ω₀²+2β)

Gdy częstotliwość zbliża się do częstotliwości rezonansowej amplituda rośnie. Wzrost amplitudy oznacza wzrost przyspieszenia i prędkości. W przypadku ciała ludzkiego rezultatem drgań o zbyt dużej amplitudzie jest ból. W ogólności drgania mogą spowodować uszkodzenia.

8.Równanie stanu gazu doskonałego, przemiany fazowe

Równanie Clapeyrona

pV=nRT

Jaką objętość powinien mieć gaz doskonały?

1.Gaz składa się z molekuł, molekuły mogą być jedno lub wielo atomowe

2.Molekuły znajdują się w ciągłym ruchu i podlegają Newtonowskim zasadom ruchu tzn. poruszają się z różnymi prędkościami i dowolnym ruchu.

3.Całkowita liczba cząsteczek jest olbrzymia, kierunki i prędkości molekuł mogą się gwałtownie zmieniać w wyniku zderzeń ze ściankami naczynia i innymi molekułami.

4.Objętości samych molekuł są bardzo małe w porównaniu z objętością zajmowaną przez gaz.

5.Pomiędzy molekułami nie działają żadne siły

6.Zderzenia molekuł są doskonale sprężyste i czas zderzeń jest bardzo krótki.

Przemiany stanu gazu doskonałego

1.Izotermiczna

T=const. PV=const.

dU =nCrdT, dT=0 wtedy dU=0

W=nRT*ln(V₁/V₂)

2.Izobaryczna

p=const.

W= -p(V₂-V₁)

3.Izochoryczna

V=const

W=0

4.Adiabatyczna

Pv=const

5.Politropowa

Przemiana, w ktorej ciepło właściwe przejmuje określoną z góry zadaną wartość.

PVⁿ=const. - równanie politropy

N=(C_P-C)/(C_V-C)

C - dowolne ciepło właściwe

N= 0 wtedy p=const.

9.Zerowa i pierwsza zasada termodynamiki

Zerowa zasada termodynamiki :

Jeżeli ciała a i b są w równowadze termicznej z trzecim ciałem c to a i b są w równowadze termicznej.

Istnieje wielkość skalarna nazywana temperaturą, która jest właściwością wszystkich układów termodynamicznych, przy czym równość temperatur jest warunkiem koniecznym i wystarczającym równowagi termicznej

I zasada termodynamiki:

W układzie odosobnionym, w którym zachodzą dowolne zjawiska mechaniczne, cieplne, elektryczne, magnetyczne, chemiczne, czy też przemiany jądrowe nie można w żaden sposób zmienić całkowitej energii układu. Jeśli mogą natomiast zachodzić wymiany energii układu z otoczeniem to przyrost lub ubytek całkowitej energii układu równa się doprowadzonej z zewnątrz lub odprowadzonej na zewnątrz energii.

U₂-U₁ = Q+W

10.Druga zasada termodynamiki - cykl Carnote'a

Silnik cieplny działający periodycznie i nie zasilany żadną inną formą energii musi pobierać ciepło ze źródła o temperaturze wyższej od najzimniejszego ciała otoczenia.

Perpetum Mobile II rodzaju jest niemożliwością

P.M. - urządzenie, które stale dostarczało by pracy kosztem ciepła pobranego z otoczenia i zamienionego całkowicie na pracę

Proces odwracalny termodynamiczny - jest to proces, po którego ukończeniu układ powraca do stanu pierwotnego po dowolnej drodze, ale tak żeby ich otoczenie powróciło do stanu pierwotnego.

Nieodwracalny proces termodynamiczny - jest to taki proces, że po jego ukończeniu nie możliwy jest powrót do stanu układu pierwotnego z równoczesnym powrotem otoczenia do stanu pierwotnego.

Cykl Carnotre'a

W tym cyklu wszystkie przemiany są odwracalne i quasi statyczne

Proces	Spręż. Adiab.	Rozpręż. Izoterm.	Rozpręż.Adiabat	Spręż izoter
Zmiana temp.	T2→T1	T1-const	T1→T2	T2-const
Wykona. Praca	W1=CV(T1-T2)	W2=RT1 ln (VB/Vc)	W3=CV(T2-T1)	W4=RT2 ln (VA/VD)
Ciepło	0	Q1-pobr.	0	Q2 odda

11.Pole grawitacyjne

Dwa dowolne ciała materialne przyciągają się w kierunku łączącej jej prostej siłą proporcjonalną do iloczynu ich mas, a odwrotnie proporcjonalną do kwadratu odległości tych ciał

F~(m₁m₂)/R²

1.Każda kulista warstwa materii o jednakowej gęstości przyciąga każde ciało leżące na zewnątrz niej tak jak gdyby jej masa była skupiona w środku.

2.Kula złożona z warstw współśrodkowych, z których każda ma jednakową gęstość przyciąga dowolne ciało tak jak gdyby masa kuli była skupiona w jej środku

F=G(m₁m₂)/R² - stała grawitacji

G=6,67*10 ^-11 (N*m²)/kg

Pole grawitacyjne jest polem wektorowym, a wielkość opisująca nam to pole to:

→ →

g = F/m

Pole grawitacyjne jest polem stacjonarnym.

Energia potencjalna grawitacji

U(r)=W_R∞= -G(m₁m₂)/r

Potencjał

V(r)=U_r/m₂= -G(m₁/r)

12.Ładunki i przewodniki w polu magnetycznym.

Pole magnetyczne - przestrzeń otaczająca magnes lub przewodnik z prądem

Ładunek próbny q₀

→ → →

F=q₀v x B

→ →→ →

F ⊥ V F ⊥ B

→ → →

F_MAX ⇒ V ⊥ B

→ → →

F_MIN=0 ⇒ V||B lub V=0

Jednostka indukcji magnetycznej

T - tesla

[B]T=Wb/m²

Wb - weber (jednostka strumienia magnet.)

Siły działające na ładunki w polu magnet.

Siła Lorentza:

→ → → →

F_L=q₀E+q₀V x B

Siła działająca na elektron - F'

→→

F'=q₀Vbsin(V,B)

→ →

q₀=e , V⊥B

F'=eVB

Siła działająca w całym przewodniku

F=nSL , F'=nSLeVB

J=nev , v=j/(ne)

F=iLB (bo l-1=1)

Wartość siły działającej na przewodnik w polu magnetycznym

→ → →

F=iL x B

Wartość siły kiedy mamy pojedyńczy ładunek

→ → →

F=q₀L x B

Kiedy przewodnik jest krzywy

→ →

F=∫dF

Układ dwóch biegunów to dipol magnetyczny

→ → → →

M=μ x B , μ - dipolowy moment magnet.

Energia dipola magnetycznego w p.magnet.

→ →→

U=-μ•B

Efekt Halla

V_H=R_HaBj , R_H=1/(ne) - stała Halla

19.Prawo Ampera i Biote'a Savarta

Krótko mówiąc prawo Ampera to zależność między natężeniem prądu „i”, a polem Magnetycznym B, która wyraża się wzorem

→→

∫ Bdl = μ₀i

Prawo Ampera stwierdza, że :

Krążenie wektora natężenia pola magnetycznego po dowolnej krzywej zamkniętej jest równe algebraicznej sumie natężeń prądów przepływających przez powierzchnię napiętą na tej krzywej.

_n → → _m

Ε H_i•Δl_i=ΕI_k

^{i=1 k=1}

Prawo Biota Savarta

dB=((μ505i)/(4π)*(dlsinθ)/(r²))

13.Podstawowe prawa geometrii optycznej - zasada Fermata.

„I” Prawo odbicia

∠α=∠α'

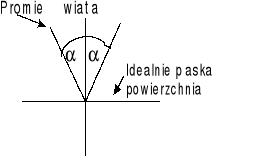
α - kąt padania, α' - kąt odbicia

promień padający, odbity i normalna do płaszczyzny odbijającej leżą w równej płaszczyźnie

Płaszczyzna chropowata :

Zjawisko rozpraszania światła

Przechodzenie światła z ośrodków

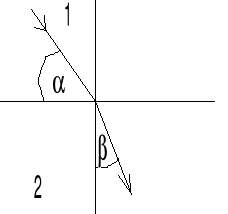
Prawo Snella

sinα/sinβ=v₁/v₂

v₁-prędkość światła w ośrodku 1

v₂-prędkość światła w ośrodku 2

Bezwzględny współczynnik załamania światła

n=C/v

C-prędkość światła w próżni

Względny współczynnik załamania światła ośrodka drugiego względem pierwszwgo

sinα/sinβ=n₂/n₁=n₂₁

„II”Prawo załamania

Promień padający, załamany i normalna leżą w jednej płaszczyźnie

v₁>v₂

Ośrodek 1 jest optycznie rzadszy od ośrodka 2

n₁>n₂

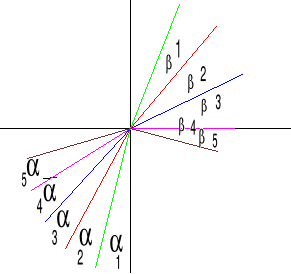
∠β₄=90°

∠α₄ - kąt graniczny (kąt dla którego kąt załamania jest równy 90°

sinα_gr/sin90°=n₂₁

sinα_gr=n₂₁

Zasada Fermata

Rzeczywista droga optyczna jaką przebywa promień świetlny między dwoma punktami jest najkrótsza spośród wszystkich możliwych dróg optycznych między tymi punktami. Drogą optyczną nazywamy iloczyn drogi geometrycznej i współczynnika załamania n-środowiska w stosunku do próżni

∫ ds/v = ∫ dt = min

Promień świetlny biegnie tak aby przebyć drogę między dwoma punktami w czasie możliwie najkrótszym.

Przejście światła przez pryzmat

Pryzmat - ciało ograniczone dwoma płaszczyznami, przecinającymi się wzdłuż prostej zwanej krawędzią pryzmatu, tworzącymi kąt ϑ zwanym kątem łączącym pryzmatu.

14.Interferencja światła

Interferencję światła zuważamy przy użyciu tzw. bipryzmatu Frensnela , który ma kąt łamiący się 0°

Wiązki światła wychodzące z pojedyńczej wąskiej szczeliny S załamują się w obydwu połówkach i wpadają na kliszę fotograficzną, w tym momencie możemy zaobserwować obraz interferencyjny złożony z jasnych i ciemnych linii.

Chciałbym też zwrócić uwagę na to że przy interferencji amplituda fali wypadkowej przyjmuje największą wartość wtedy gdy różnica dróg przebytych przez fale składowe jest równa całkowitej wielokrotności długości fali.

15.Dyspersja, absorbcja i dyfrakcja światła

Dyspersja - zjawisko widmowego rozkładu światła towarzyszące załamaniu defrakcji lub interferencji światła. Nazywa też się nią zależność współczynnika załamania ośrodka od częstotliwości światła.

Absorbcja światła - straty energii wiązki świetlnej przechodzące przez substancję, będące wynikiem przemiany energii strumienia świetlnego w różne rodzaje energii wew. Substancji, albo w energię wtórnego promieniowania wysyłanego w innym kierunku.

Dyfrakcja światła - występuje podczas rozchodzenia się światła w ośrodkach optycznie niejednorodnych , a w szczególności podczas przechodzenia przez niewielkie otwory lub w pobliżu ostrych krawędzi ciał przeźroczystych lub nieprzeźroczystych

Np. oświetlanie punktowym źródłem, kołowego otworu w nieprzeźroczystej przesłonie.

16.Polaryzacja światła przez odbicie i podwójne załamanie.

Fale elektromagnetyczne są falami poprzecznymi, co stwarza możliwość ich polaryzacji.

Światłem spolaryzowanym całkowicie , nazywa się takie światło dla którego istnieją określone związki między fazami wzajemnie prostopadłymi.

Światło może być częściowo lub całkowicie spolaryzowane poprzez odbicie się od materiału zbudowanego z płytek polaryzacynych.

Np.okulary przeciwsłoneczne

17. Rodzaje oddziaływań w przyrodzie.

W fizyce wyróżnia się 4 rodzaje oddziaływań cząstek pomiędzy ciałami

• działanie grawitacyjne (źródłem jest masa-najsłabsze z całej 4-rki

• słabe jądrowe

• elektromagnetyczne źródłem jest ładunek elektryczny i najczęściej występują w przyrodzie

• oddziaływanie silne jądrowe-utrzymują jądro w całości

18. Zasada zachowania dynamiki Newtona dla ruchu obrotowego.

Jeżeli na bryłę sztywną nie działa żaden moment siły lub momenty sił się równoważą to ciało pozostaje w spoczynku lub porusza się ruchem obrotowym jednostajnym.

3. II Druga zasada zachowanie dynamiki Newt. Dla ruchu obrotowego.

Jeżeli na ciało działa niezrównaoważony moment siły to ciało porusza się ruchem obrotowym jednostajnie przyspieszonym z przyspieszniem epsilon proporcjonalnym do działającego momentu siły M i odwrotnie prop. Do mom bezwładności ciała J

19. Dla ruchu postępowego I zasada

Jeżeli na ciało nie działa żadna siła albo siły działające na to ciało się równoważą to ciało pozostaje w spoczynku lub porusza się ruchem jednostajnym.

5. II Zasada ruchu postepowego.

Jeżeli na ciało działa siła niezrównoważona to ciało porusza się ruchem jednostajnie przyspieszonym z przyspieszeniem a prop. Do działającej siły i odwrotnie prop. Do masy ciała.

20. III Zasada ruchu postępowego tzw. Akcji reakcji.

Jeżeli ciało a działa na ciało b pewną siłą f to ciało b oddziałuje na ciało a taką samą siłą co do wartości i kierunku ale przeciwnym zwrocie.

21. Zjawisko rezonansu.

Zjawisko pobudzania układu do drgań przez okresowo powtarzające się impulsy o częstotliwości drgań własnych układu. W wyniku rezonansu (jeżeli nie ma tłumienia) gwałtownie rośnie amplituda drgań układu pobudzonego co może doprowadzić do jego zniszczenia.

22. Interferencja fal sprężystych.

Wszystkie zjawiska które są wywołane przez niezakłócone nakładanie się fal. W wyniku interferencji fale mogą się wzmacniać jeżeli spotykają się w zgodnych fazach lub wygasać jeżeli spotykają się w przeciwnych fazach.

23. Równanie Wandervalsa dla n-moli.

pV=RT

24. Cykl Carnot`a

patrz zeszyt

25. Prawo Columba

Dwa elektryczne ładunki punktowe q1 i q2 oddziałują na siebie wzajemnie siłą działającą wzdłuż lini łączącej te ładunki wprost prop. Do iloczynu ich wielkości i odwrotnie prop. Do kwadratu odległości między nimi oraz zależną od środowiska w którym te ładunki się znajdują.

26. Prawo Gaussa

strumień pola elektrostatycznego przechodzącego przez dowolną powierzchnie zamkniętą jest równa algebraicznej sumie wszystkich ladunków elektrycznych znajdujących się wewnątrz tej powierzchni

Q - ładunek elektryczny

Eps 0 - przenikalność elek. W próżni

Eps r - przenikalnoś elektr.

27.Widmo fal elekrtomag.

Patrz zeszyt

28.Zjawisko fotoelektr.

I zew. polega na wybijaniu elektronów z pow. metali przez kwanty promieniowania elektromag. (fotony). Zależność między energią wybijanych elektronów a energią fotonów opisuje prawo Einsteina - Millikana . Zjawisko fotoelektryczne zew. Było pierwszym zaobserwowanym efektem świadczącym o kwantowej naturze promieniowania elektromag.

II wew. Polega na podwyższeniu energii elektronów w półprzewodnikach pod wpływem promieniowania elektromag. , dzięki czemu elektrony te przechodzą do pasma przewodnictwa i powodują zmniejszenie oporu przewodnika

29. Model atomu wg. Bohra (książka niebieska)

Promieniowanie ciala doskonale czarnego.

W 1900 max plank przedstawil wzor empiryczny opisujacy widmowa zdolnosc emisyjna atomu

1, oscylator nie moze miec dowolnej energi lecz tylko energie dane wzorem e=nhv gdzie v oznacza czestosc oscylatora h stala(zwana stala planca n pewna liczbe calkowita zwana liczba kwantowa.

z powyzwszego wzoru wynika zw energia jest skwantowana i moze przyjmowac tylko scisle okreslone wartosci.

2. oscylator nie wypromieniuje energii w sposob ciagly lecz porcjami czyli kwantami. Kwanty emitowane sa gdy oscylator z jednego stanu do do danej energii do drugiego o innej energii

dopoki oscylator poostaje w jednym ze swoich stanow kwantowych dopoty ani nie emituje ani nie absorbuje energii

jezeli enrgia jest skwantowana to jej zmiany dokonuja sie skokowo przy czym deltaE = hv. wzgledna zmiana energi wynosi wiec deltaE/E=4,7razy 10 do -31

---