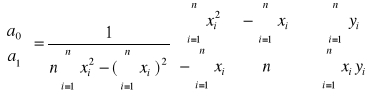Funkcja regresji - opisuje liczbowo zależność pomiędzy zmiennymi niezależnymi (x) oraz zmienną zależną (y)

Równanie stochastyczne regresji

; zapis wektorowy:

i - numer obserwacji

k - numer zmiennej objaśniającej (niezależnej)

- składnik losowy

α₀, α₁, ..., α_k - parametry strukturalne

Równanie deterministyczne regresji

; zapis wektorowy:

a₀, a₁, ..., a_k - oszacowane oceny parametrów strukturalnych

- wektor wartości teoretycznych

Etapy analizy regresji dla funkcji postaci

1. Oszacowanie wektora a metodą MNK

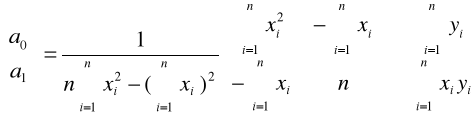
Interpretacja a₁: wzrost zmiennej x o 1 jednostkę powoduje wzrost(spadek) zmiennej y o a₁ jednostek.

2. Wyznaczenie współczynnika determinacji R²

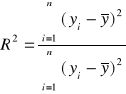
lub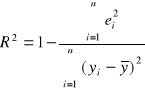

- reszty emipryczne

Interpretacja R²: obliczony współczynnik determinacji informuje, że zmiany zmiennej x objaśniają zmiany zmiennej y w R² procentach.

- współczynnik zbieżności określa w jaki sposób zmienność zmiennej y nie została wyjaśniona za pomocą oszacowanej funkcji regresji.

3. Obliczenie wariancji resztowej S_e²

4. Obliczenie standardowych błędów szacunku S(a₀) i S(a₁)

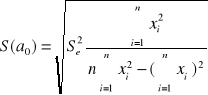
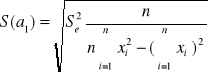
Interpretacja S(a₀) : Przyjmując ocenę estymatora wyrazu wolnego a₀ średnio mylimy się o S(a₀).

Interpretacja S(a₁) : Przyjmując ocenę a₀ parametru stojącego przy zmiennej x₁ średnio mylimy się o S(a₁).

5. Wyznaczenie przedziałów ufności nieznanych parametrów strukturalnych α₀ oraz α₁

t_α - wartość statystyki t-studenta o n-(k+1) stopniach swobody, dla zadanego α

Interpretacja: taka jak dla przedziałów ufności

6. Weryfikację hipotez o istotności parametrów modelu

Test t-Studenta

Badamy dla każdego parametru strukturalnego osobno, czy istotnie różni się on od zera. Jeśli nie uda nam się odrzucić hipotezy zerowej, będzie to oznaczało, że zmienna objaśniająca przy której stoi dany parametr nie wpływa na zmienną objaśnianą, więc można ją usunąć z modelu (jednakże to wymaga powtórnego oszacowania modelu, z już z aktualnym zestawem zmiennych objaśniających).

H₀: α_j = 0

H₁: α_j ≠ 0 lub H₁: α_j > 0 lub H₁: α_j < 0 lub

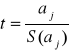
Obszary odrzucenia w zależności od postaci H₁ konstruujemy tak, jak dla wszystkich testów t-studenta, przy n-(k+1) stopniach swobody, zwykle dla poziomu istotności 0,05.

Własności funkcji regresji:

Mając
oraz

Praca pochodzi z serwisu www.e-sciagi.pl <<<>>> Zacznij zarabiać http://partner.e-sciagi.pl