Próbkowanie Sygnałów
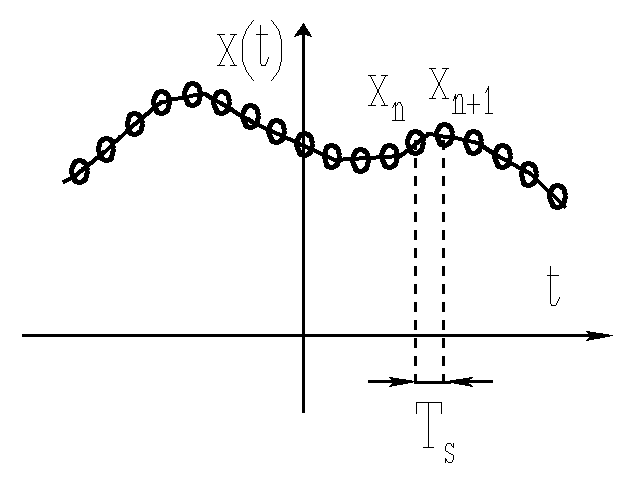
Próbkowanie polega na pobieraniu wartości xn sygnału w pewnych odstępach. Zazwyczaj odstępy są stałe. Oznaczając je przez Ts otrzymuje się
![]()
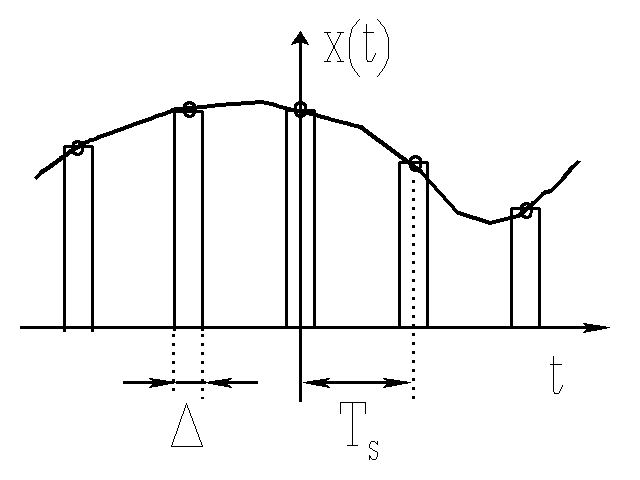
Przedział [t0, t0+nTs] stanowi okno czasowe, w którym pobierane są próbki. Praktyczna realizacja próbkowania polega na pobieraniu wąskich impulsów o szerokości Δ i amplitudzie xn.
Twierdzenie (o próbkowaniu)
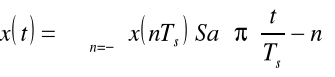
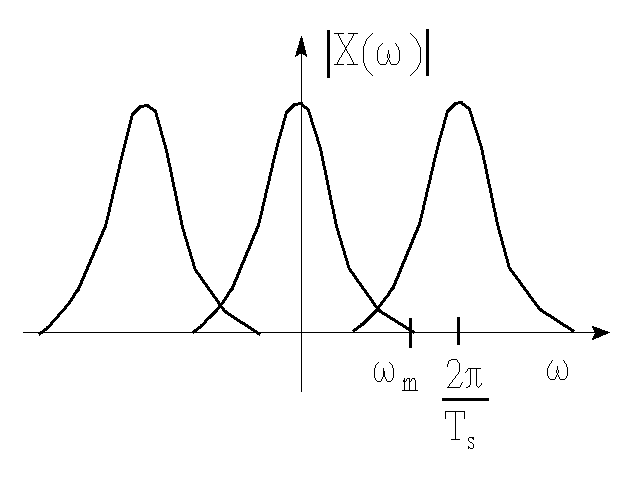
Jeżeli x(t) jest sygnałem, którego widmo X(ω) spełnia warunek X(ω)=0 dla |ω|≥ωm, to zbiór próbek {x(nTs)} tego sygnału odległych od siebie o stały przedział Ts<π/ωm, jednoznacznie określa sygnał x(t), mianowicie
Jest to szereg Shannona. W literaturze rosyjskiej nazywany szeregiem Kotielnikowa. Sygnał x(t) jest nazywany sygnałem o uciętym widmie.
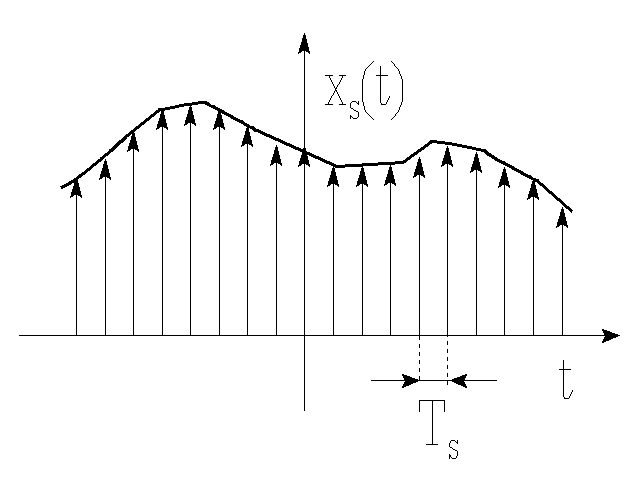
Dowód
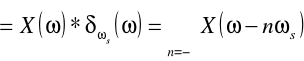
Sygnał jest teoretycznie próbkowany punktowo ciągiem impulsów Diraca δTs(t). Sygnał spróbkowany ma postać x(t)⋅δTs(t). Widmo Xs(ω) sygnału spróbkowanego jest równe
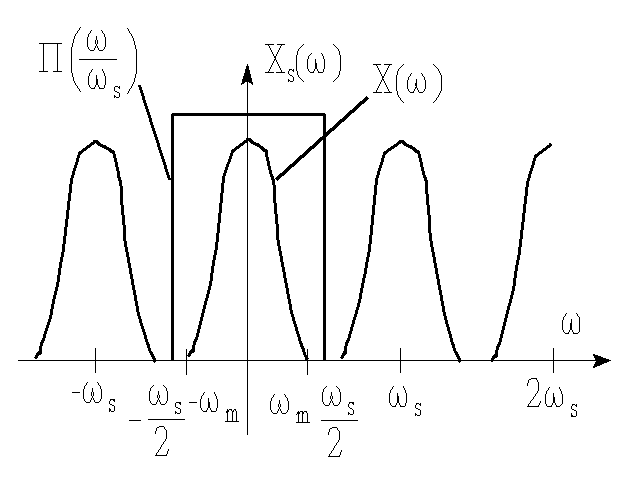
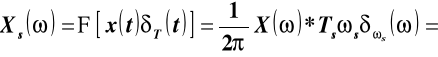
Filtrując widmo sygnału idealnym filtrem dolnoprzepustowym o transmitancji H(ω)=Π(ω/ωs), gdzie ωm<ωs/2<ωs-ωm otrzymujemy sygnał o widmie X(ω) a więc sygnał x(t).
Interpretacja
Minimalna częstotliwość próbkowania, odpowiadająca przedziałowi Ts=π/ωm , nazywana jest częstotliwością Nyquista fN =2 fm=ωm/π . Jest ona dwa razy większa odgórnej częstotliwości granicznej fm sygnału x(t).
Widmo sygnału spróbkowanego xs(t) jest wielokrotnym powieleniem widma sygnału x(t) w odstępach równych częstotliwości próbkowania fs .
Przykład
Człowiek nie słyszy sygnałów akustycznych o częstotliwościach powyżej 20kHz. Dlatego, po odfiltrowaniu wyższych częstotliwości, sygnał taki można próbkować z częstotliwością nie mniejszą niż fN=40kHz, a zatem w odstępach nie większych niż T=25μs. Można oczywiście zastosować większą częstotliwość próbkowania, ale zwiększa się wówczas ilość próbek i miejsce potrzebne na ich zapisanie. Na CD-ROM stosuje się częstotliwość 44,1kHz.
Szereg Shannona
Funkcje {Sa[π(t/Ts-n)]} stanowią dla całkowitego n∋(-∞,∞) zbiór zupełny funkcji wzajemnie ortogonalnych, czyli stanowią bazę. Współczynniki szeregu są wartościami sygnału w punktach odległych o Ts, czyli próbkami xn sygnału x(t). Szereg ten jest szeregiem interpolacyjnym, gdyż można obliczyć wartości funkcji x(t) w punktach pośrednich pomiędzy kolejnymi wartościami xn.
Czas trwania sygnału a szerokość widma
W praktyce sygnał możemy próbkować jedynie w skończonym przedziale czasu, a więc liczba próbek jest skończona. Sygnały impulsowe, różne od zera tylko w skończonym przedziale czasu mają widma nieskończone. Nie spełniają one założeń twierdzenia o próbkowaniu. W rzeczywistości próbkujemy je i odtwarzamy w przybliżeniu. Można pokazać, że istnieje dla szerokiej klasy sygnałów zależność między czasem trwania ΔT określonym jako
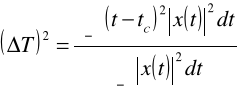
a szerokością widma określoną następująco
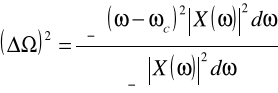
gdzie tc i ωc są odciętymi środków ciężkości kwadratów modułów |x(t)|2 i |X(ω)|2. Mianowicie
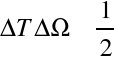
Nierówność ta zwana jest zasadą nieoznaczoności, gdyż podobna jest do zasady Heisenberga twórcy mechaniki kwantowej.
Odtwarzanie sygnału z próbek
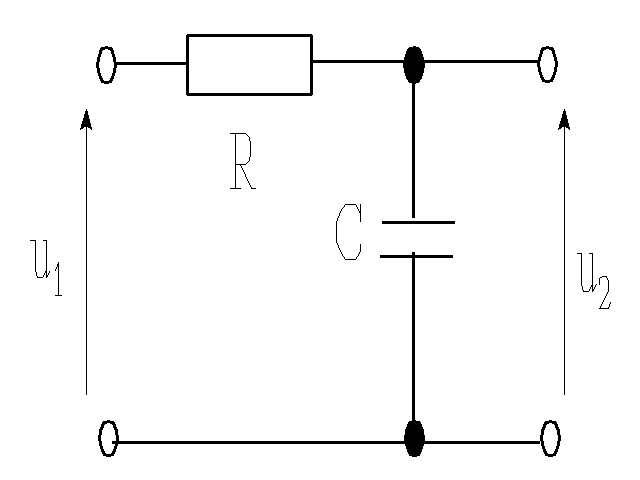
Sumy częściowe szeregu Shannona są bardzo niedogodne do odtwarzania sygnału. Dlatego postępuje się inaczej. Prostą metodą jest zastosowanie układu podtrzymującego - układu całkującego RC.
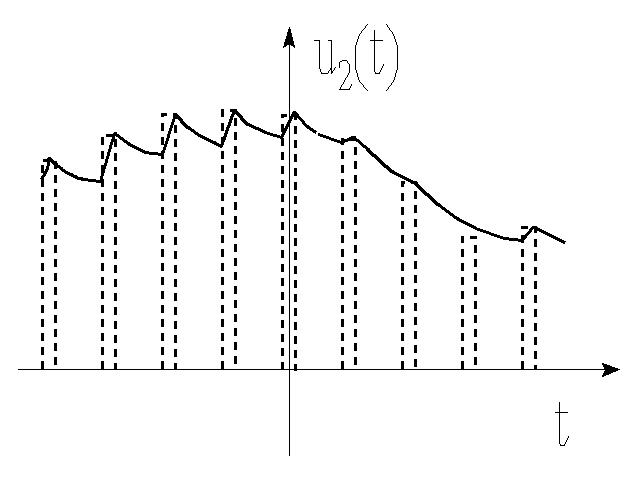
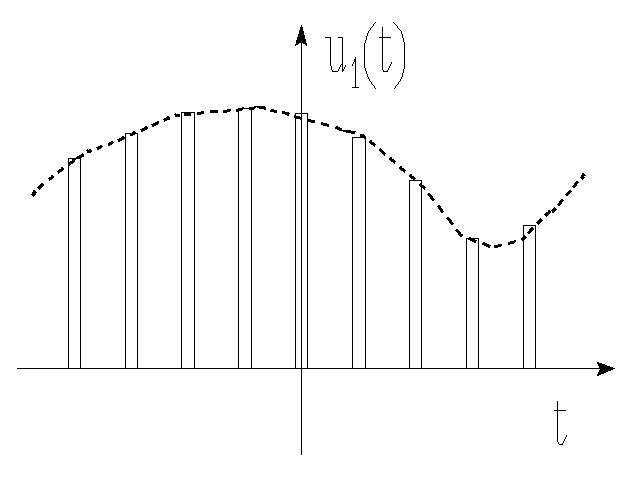
Stała czasu układu τ =RC oraz szerokość impulsów musi być dobrana tak, aby kondensator zdążył się naładować do napięcia równego wartości próbki i z drugiej strony zdążył się rozładowywać, gdy wartość próbek maleje. Dlatego stosuje się czasem bardziej skomplikowane układy dające rezultat jak na rysunku.
Błędy próbkowania
Aliasing
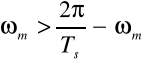
Jest to nakładanie się widm powielanych spowodowane zbyt małą częstotliwością próbkowania
Jitter
Są to drobne przesunięcia (drżenie) punktów próbkowania w stosunku do położeń równomiernych 2πn/Ts.
Kwantowanie
Wartości próbek są zaokrąglane do jednej z wartości z wcześniej ustalonego zbioru {qn} w celu zapisu cyfrowego. Różnica rzeczywistych wartości xn i wartości skwantowanych qn stanowi tzw. szum kwantowania.
Ucięcie sygnału
Nie bierzemy wszystkich próbek sygnału a tylko z ograniczonego okna czasowego.
SYSE_Folie Bohdan Butkiewicz
SYS7_Probkow.doc 3
![]()
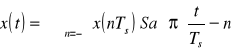
![]()
![]()
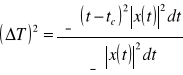
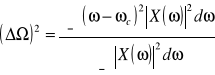
![]()
![]()
Wyszukiwarka
Podobne podstrony:
PRÓBKOWANIE SYGNAŁU - Sprawozdanie z laboratorium Technologia Informacjna, Automatyka, Semestr 1, Te
Smoku, Automatyka, Semestr 1, Technologie informacyjne
MATLAB - Sprawozdanie z laboratorium Technologii Informacyjnych, Automatyka, Semestr 1, Technologie
Pytania- Technologia Informacyjna, Automatyka i robotyka air pwr, I SEMESTR, Technologia informacyjn
2010 Grudzień 6, Rok I, Semestr I, Technologia Informacyjna
Strona tytulowa referatu, Administracja, Semestr 1, Technologia informacyjna
KWERENDY dod 2, Szkoła, Semestr 1, Technologia informacyjna, Ćwiczenie 6
inf, SGGW, Niezbędnik Huberta, Leśnictwo, Semestr 1, Technologia Informacyjna, Egzamin
grafika, wszop ZZIP, II semestr, Technologia informacyjna, Technologia produkcyjna 1
infa test 1, Budownictwo PK, I ST. (2008-2012), Semestr 1, Technologia Informacyjna
tech. ifn. ćw, ^ Turystyka i Rekreacja GWSH Katowice, 2 semestr, technologia informacyjna
Najważniejsze zagadnienia - Moduł 3, Semestr I, Technologie informacyjne, Moduł 3
Kolokwium TI, Politechnika Wrocławska Energetyka, 1 semestr, Technologie Informacyjne
TI -wyklad 2, Studia - Mechatronika, I semestr, Technologia Informacyjna
kilka pytan z egzaminu 2010 INFA, Studia WZR zarządzanie 2013-2014, semestr I, Technologia Informacy
INFAQ, Studia WNOŻ SGGW 2008-2013, Inżynierskie, Semestr 1, Technologia informacyjna
inf-sciaga, SGGW, Niezbędnik Huberta, Leśnictwo, Semestr 1, Technologia Informacyjna, Egzamin
zagadnienia Excel, I semestr, Technologia informacyjna
Technologia informacyjna, Semestr 1, Technologia informacyjna
więcej podobnych podstron