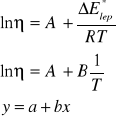Część teoretyczna

Istnienie sił przyciągania międzycząsteczkowego w cieczy powoduje, że przepływ cieczy ze stałą szybkością wymaga przyłożenia siły, która zrównoważy tarcie wewnętrzne przeciwstawiające się przepływowi cieczy. Siłę tę definiuje równanie Newtona:

(1)

Gdzie: F-siła powodująca względny ruch równoległych do siebie warstw cieczy

S - pole powierzchni warstw

dv/dx - gradient prędkości, prostopadły do kierunku przepływu cieczy

ŋ - współczynnik proporcjonalności, zwany współczynnikiem lepkości dynamicznej ośrodka

Lepkość jest to siła tarcia, która powoduje, że dwie warstwy o powierzchni jednostkowej odległe od siebie o jednostkową odległość poruszają się z gradientem prędkości dv/dx = 1s^-1

Lepkość cieczy maleje ze wzrostem temperatury. Zależność płynności cieczy(płynność jest odwrotnością lepkości)od temperatury jest wykładnicza i opisuje ją równanie Arrheniusa:

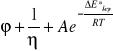
(2)

Gdzie: φ - płynność cieczy

∆E*_lep - molowa energia aktywacji lepkiego przepływu cieczy

R - stała gazowa

T - temperatura w skali Kelvina

1. stała równania Arrheniusa

Wielkość ∆E*_lep ma sens fizyczny bariery energetycznej, którą 1 mol cząsteczek musi pokonać przeciskając się do dalszego położenia w rurze. Stanowi ona w przybliżeniu 1/3 molowej energii parowania. Współczynnik
jest nazwany współczynnikiem Boltzmanna i określa ułamek cząsteczek o energii równej lub przewyższającej energię lepkiego przepływu. Logarytmując równanie Arrheniusa otrzymujemy wzór:

(3)

Gdzie: A' i B - stałe, zależne od rodzaju cieczy.

Zależność
w niewielkich przedziałach temperatury wykazuje charakter liniowy, a wyrażenie
jest współczynnikiem kierunkowym otrzymanej prostej. Pomiar lepkości cieczy w kilku temperaturach pozwala zatem na obliczenie energii aktywacji lepkiego przepływu.

Dokładniejszy opis temperaturowej zależności lepkości czystych niezdysocjowanych cieczy daje równanie Eyringa:

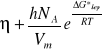
(4)

Gdzie: h - stała Plancka

N_A - liczba Avogadro

V_m - objętość molowa cieczy

Molowa entalpia swobodna aktywacji lepkiego przepływu.

Równanie to zostało wprowadzone w oparciu o model cieczy zaproponowany przez Eyringa i współpracowników. W modelu tym zakłada się, ze ciecz ma strukturę dziurową. Oznacza to, że pewna ilość węzłów sieci jest nieobsadzona przez cząsteczki. Cząsteczki mogą zatem przeskakiwać ze swojego położenia równowagi do najbliższej dziury. Proces taki wymaga pokonania przez cząsteczkę bariery potencjału równej ∆G*_lep (w przeliczeniu na 1 mol). Korzystając z ogólnej zależności termodynamicznej:

(5)

Równanie (4) można napisać w postaci:

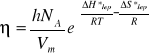
(6)

Gdzie: ∆H*_lep - molowa entalpia aktywacji lepkiego przepływu,

∆S*_lep -molowa entropia aktywacji lepkiego przepływu.

Wielkości V_m oraz są stałe w danej temperaturze, a zatem równanie redukuje się do postaci:

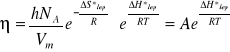
(7)

Zważywszy, ze w przypadku faz skondensowanych:

(8)

Równanie (7) jest identyczne z równaniem Arrheniusa (2). Entropia lepkiego przepływu ∆S*_lep jest tym większa im struktura badanej cieczy jest bardziej uporządkowana. Zatem, dla cieczy zasocjowanych, jak np. woda i alkohole obserwuje się wyższe wartości entropii aktywacji lepkiego przepływu, niż dla cieczy niezasosjowanych. Entropię aktywacji lepkiego przepływu ∆S*_lep w danej temperaturze można obliczyć z równania (5) jeśli wcześniej wyznaczy się eksperymentalnie ∆G*_lep i ∆H*_lep.

Wyznaczenie entalpii swobodnej aktywacji lepkiego przepływu ∆G^*_lep badanej cieczy

Opracowanie wyników:

Wyznaczam gęstość izopropanolu w temperaturze pomiaru tp (w skali Celsjusza) korzystając z równania:

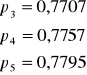
Obliczam lepkość alkoholu izoproplylowego η [P] w każdej temperaturze z równania:

Wykorzystując wartość stałej kapilary K[P cm^-3 g^-1s^-1] oraz średni czas przepływu cieczy t

Obliczam objętość molową alkoholu izopropylowego V_m we wszystkich temperaturach na podstawie poniższej zależności, w której M jest masą molową izopopanolu:

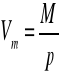
Obliczam swobodną entalpię aktywacji lepkiego przepływu ∆G^*_lep w badanych temperaturach ze wzoru Eyringa, przekształconego do postaci:

gdzie:R=8,314J/molK- stała gazowa

T-temperatura [K]

Η-lepkość izopropylu

V_m - objętość molowa

H - stała Plancka = 6,625 10^-27

N_A - liczba avogadro = 6,02 10²³

Wyznaczam entalpie aktywacji lepkiego przepływu ∆H^*lep cieczy badanej Wyznaczam metodą najmniejszych kwadratów współczynnik kierunkowy prostej Bnum

Wyznaczam metodą graficzną współczynnik prostej B_graf

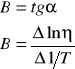
Obliczam entalpię aktywacji lepkiego przepływu ∆H^*_lep korzystając z zależności:

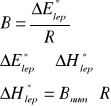
Wyznaczam entropie aktywacji lepkiego przepływu ∆S^*_lep cieczy badanej

Obliczam entropie aktywacji lepkiego przepływu ∆S^*_lep we wszystkich temperaturach wykorzystując zależność

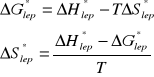
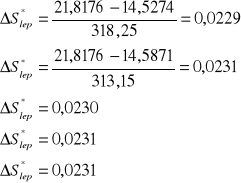
Tabela wyników obliczeń:

Tp [°C]	Tp=T [K]	T^-1 [K^-1]	N [P]		Ln n	P [gcm^-3]	Vm [cm^3mol^-1]		∆G^*lep [KJ mol^-1]	∆S^*lep [KJ mol^-1]
45,1	318,25	0,003142	0,01224		-4,4027	0,7613	78,9476		14,5274	0,0229
40	113,15	0,003193	0,01379		-4,2840	0,7662	78,4456		14,5871	0,0231
35,1	308,25	0,003244	0,01599		-4,1357	0,7707	77,9841		14,7238	0,0230
29,5	302,65	0,003304	0,01858		-3,9856	0,7757	77,4809		14,8177	0,0231
25,2	298,35	0,003352	0,02114		-3,8564	0,7795	77,1116		14,9157	0,0231
Bgraf				Bnum				∆H^*lep
2606,51				2624,2				21,8176

Wnioski:

Od temperatury zależy gęstość, objętość molowa, lepkość i swobodna entalpia lepkiego przepływu. Wraz ze wzrostem temperatury rośnie objętość molowa cieczy natomiast gęstość izopropylu, lepkość i wartość swobodnej entalpii lepkiego przepływu maleją.

Niezależna od temperatury jest entalpia . Jest ona równa w przybliżeniu molowej energii aktywacji lepkiego przepływu i nie ulega zmianie podczas zmian temperatury.

---