PODSTAWOWE METODY OPRACOWANIA WYNIKÓW POMIARÓW
Rodzaje błędów pomiarowych
Podczas pomiaru zachodzi zawsze oddziaływanie pomiędzy przyrządem pomiarowym a układem badanym. Wynikiem takiego oddziaływania może być zaburzenie układu obserwowanego, a więc zmiana jego stanu. Przykładowo, gdy mierzymy temperatur* wody za pomocą termometru rtęciowego, to pomiędzy wodą a termometrem zachodzi oddziaływanie polegające na wymianie pomiędzy nimi pewnej energii w postaci ciepła. W rezultacie tej wymiany temperatura wody nieco się zmienia; stan układu ulega zmianie, czyli zaburzeniu.
Zawsze musimy tak dobiera* przyrządy i metody pomiarowe, aby zaburzenie wielkości mierzonej było znacznie mniejsze od niepewności, z jaką wielkość tę wyznaczamy. Rzecz* oczywistą jest, iż używane przyrządy muszą być wykorzystywane zgodnie z instrukcjami ich obsługi (np. podstawa wagi analitycznej musi być ustawiona dokładnie poziomo, waga nie może znajdować się blisko *r*de* ciepła, stolik, na którym ona stoi, nie powinien podlegać drganiom).
W przypadku gdy zaburzenie wprowadzane przez dostępne metody pomiarowe jest nieuchronne, możemy próbować je oceni* i wprowadzi* odpowiedni* poprawkę do wyniku opisującego wielkość mierzoną. Poprawek nie można stosować do wyników pomiaru wielkości mikroskopowych, gdy zaburzenie przez pomiar jest tego samego rzędu co wielkość mierzona.
Wykonuj*c pomiar uzyskujemy wynik, którego wartość zawsze obarczona jest pewną niepewności* wynikaj*c* chociażby z precyzyjności wycechowania używanego miernika. Poza tym wyniki pomiarów r**ni* się od rzeczywistych wartości mierzonych wielkości wskutek występowania błędów pomiarowych. Błędy te dzielimy na: błędy grube, błędy systematyczne oraz błędy przypadkowe.
Z błędem grubym mamy do czynienia np. w przypadku, gdy dokonuj*c wielokrotnie pomiaru tej samej wielkości zarejestrujemy w*r*d uzyskanych wyników wartość znacznie r**ni*c* się od pozostałych. Przyczyn* takiego faktu może być nieuwaga lub niestaranność wykonującego pomiary, przekłamanie przy zapisie uzyskanego wyniku lub nieoczekiwana i niezauważona zmiana warunków pomiaru w trakcie rejestracji wyniku obarczonego błędem grubym. Istotne jest, iż nawet pobieżna analiza uzyskanych wyników pozwala wykryć te spośród nich, które obarczone są błędami grubymi.
Błędami systematycznymi nazywamy takie błędy, którymi w jednakowym stopniu obarczone są wszystkie zarejestrowane wyniki pomiar*w. Przyczyn* wystąpienia tego typu błędów może być z*e wyzerowanie lub wyskalowanie przyrządu pomiarowego (np. trywialne wykrzywienie wskazówki w mierniku analogowym). Inną przyczyn* może być stosowanie niewłaściwej metody pomiarów. Przykładowo: sędzia znajdujący się na mecie biegu na 100 m rozpoczyna pomiar czasu biegu w momencie usłyszenia wystrzału pistoletu startowego. W takim przypadku każdy zarejestrowany wynik będzie krótszy od rzeczywistego czasu, jaki zużył sprinter na pokonanie dystansu 100 m o czas jaki potrzebował dźwięk wystrzału na dotarcie od pistoletu do ucha sędziego. Biorąc pod uwag* prędkość propagacji fali akustycznej w powietrzu można oszacować r**nic* pomiędzy tak zmierzonym czasem biegu a jego rzeczywistym czasem. Różnica ta w warunkach normalnych wyniesie około 0,3 s. Inną przyczyną błędu systematycznego może być niewłaściwie funkcjonujący (np. opóźniający się) stoper.
W przypadku wyników pomiaru obarczonych błędem systematycznym istotne jest to, iż możemy w wyniku analizy warunków przeprowadzenia pomiarów (metody pomiarowej oraz stosowanej aparatury) ocenić wielkość błędu systematycznego i w ten sposób uzyskać lepsze przybliżenie prawidłowego wyniku.
Wartości błędów przypadkowych, jak sama nazwa wskazuje, którymi zawsze obarczone są wyniki pomiar*w, nie dają się przewidzieć co do swej rzeczywistej wartości dla konkretnego, pojedynczego wyniku pomiaru. Źr*d*em tych błędów jest najczęściej działanie bardzo wielu drobnych i zmiennych czynników o charakterze losowym, których nie potrafimy ani przewidzieć ani usuną*. O istnieniu błędów przypadkowych świadczy niepowtarzalność wyników pomiaru jednej i tej samej wielkości, np. czasu spadku kawałka kredy z wysokości 1 m. Gdy wiele os*b będzie jednocześnie mierzy*o ten czas, to uzyskaj* z reguły różne wyniki. Podobnie, gdy jedna osoba będzie wielokrotnie powtarza*a ten sam pomiar, to tak*e w różnych próbach uzyska wyniki różniące się między sobą. Przyczyn* wystąpienia błędów przypadkowych w przytoczonych przykładach jest pewna "przypadkowo**" szybkości zadziałania wykonującego pomiar. Jego refleks zależy nie tylko od specyficznych, indywidualnych predyspozycji, ale tak*e od chwilowych czynników takich, jak: stopie* koncentracji, zmęczenie itp.. W przypadku innych eksperymentów *r*dłem błędów przypadkowych mogą być np. fluktuacje strumienia powietrza powodującego ruchy zwierciadełka w galwanometrze zwierciadlanym, fluktuacje natężenia promieniowania emitowanego przez atomy materia*u poddawanego analizie spektralnej.
Niekiedy parametr określający dokładność wyników pomiarów (czyli parametr nazywany w niniejszym skrypcie niepewności* wyniku pomiaru) bywa nazywany "błędem pomiarowym". Jest to nazwa myl*ca, ponieważ w potocznym znaczeniu błędem nazywamy różnic* pomiędzy daną wartości* a wartości* rzeczywistą. Z tego względu Międzynarodowa Organizacja Metrologii Prawnej oraz Międzynarodowy Komitet Miar i Wag sugerują stosowanie terminu "niepewność pomiarowa" (w języku ang. uncertainty, franc. incertitude). W metrologii niepewność wyniku nazywana jest także granicznym błędem pomiaru lub niedokładności* pomiaru. Niepewność bezwzględna ma postać ![]()
tak*, że
![]()
lub ![]()
(1)
gdzie ![]()
- błąd pomiaru, P{..} - prawdopodobieństwo zdarzenia w klamrze, ![]()
- zakładana minimalna wartość prawdopodobieństwa tego, iż b**d pomiaru ![]()
jest mniejszy od niepewności ![]()
.
Wartość i niepewność wyników pomiarów bezpośrednich
Istotne w przypadku wyników obarczonych błędami przypadkowymi jest to, iż ich wartości oscylują wokół pewnej wartości średniej ![]()
określonej prostym wzorem:
(2)
gdzie ![]()
oznaczaj* wyniki kolejnych pojedynczych pomiarów wielkości fizycznej, n - liczba tych pomiar*w, i - numer kolejnego pomiaru.
Niepewność wyniku wynikającego z występowania błędów przypadkowych opisuje tzw. odchylenie standardowe ![]()
wartości średniej serii pomiarów (zwane niekiedy błędem *rednim kwadratowym wartości średniej serii pomiar*w)
(3)
Wielkość ta pozwala określić przedział wartości od ![]()
do ![]()
, w którym znajduje się ponad 68,2 % wyników pomiarów. Oznacza to, iż 68,2 % wyników nie jest obarczonych większym błędem przypadkowym ni* ![]()
. Natomiast 95,4 % wyników pomiarów nie jest obarczonych błędami większymi od ![]()
.
Odchylenie standardowe oddaje statystyczny charakter natury błędów przypadkowych. Dokonuj*c wielu pomiarów można uzyskać niewielką wartość tej wielkości. Tymczasem niepewność uzyskanego wyniku zależy nie tylko od sumienności i pracowitości eksperymentatora (liczby pomiar*w), lecz także od precyzji używanego przyrządu pomiarowego. Inne są dokładności wyników pomiarów określonej d*ugości dokonanych za pomocą przymiaru krawieckiego, suwmiarki oraz interferometru optycznego. Niepewność wyniku pomiaru dokonanego danym przyrządem najczęściej określana jest współczynnikiem zwanym klas* dokładności przyrządu. Jego wartość odpowiada względnej niepewności wyniku pomiaru wyrażonej w procentach przy pomiarze z użyciem danego zakresu pomiarowego. Gdy więc dokonujemy pomiaru przyrządem o klasie k na zakresie Z, to niepewność wyniku pojedynczego pomiaru ![]()
wyznacza się korzystaj*c że wzoru:
![]()
(4)
W przypadku niektórych przyrządów pomiarowych, np. mierników posiadających wyświetlacze cyfrowe, na precyzje dokonanego pomiaru wpływa tzw. b**d rozdzielczości. B**d ten wynika z faktu, iż mierzona wielkość jest przedstawiana w postaci jej reprezentacji cyfrowej o skończonej liczbie cyfr. Niepewność tego przedstawienia odpowiada z reguły wartości jednostki ostatniej pozycji zapisu dziesiętnego wyniku przedstawianego na wyświetlaczu cyfrowym.
Często niepewność pojedynczego pomiaru jest definiowana przez producenta miernika jako suma niepewności związanych z wartości* mierzoną, zakresem pomiarowym oraz błędem rozdzielczości. Wyznaczaj*c niepewność wyników należy każdorazowo zapoznać się z instrukcją obsługi danego, nawet najprostszego miernika, w której producent określa dokładność pomiaru wynikaj*cą z konstrukcji przyrządu.
Biorąc pod uwag*, iż dokładność wyznaczenia danej wielkości zależy zarówno od liczby dokonanych pomiar*w, jak i od klasy dokładności stosowanych przyrządów pomiarowych, całkowite odchylenie standardowe ![]()
uzyskanego wyniku oblicza się zazwyczaj ze wzoru:
(5)
gdzie ![]()
oznacza odchylenie standardowe wartości średniej serii pomiar*w, ![]()
- niepewność wyniku pomiaru związaną z klasą dokładności użytego przyrządu pomiarowego.
Niepewność wyników pomiarów pośrednich
Do tej pory analizowali*my sposób określania niepewności pomiarów bezpośrednich, w czasie których dokonywane jest "porównanie" wielkości mierzonej ze wzorcem. Znacznie częściej dokonywane są pomiary pośrednie. Wymagaj* one pomiaru kilku wielkości fizycznych związanych z wielkości* wyznaczaną pewnym prawem fizycznym, wyrażonym przez odpowiedni związek matematyczny. Przykładem pomiarów bezpośrednich jest pomiar d*ugości. Przykładem pomiarów pośrednich jest wyznaczanie rezystancji R opornika na podstawie wyznaczenia natężenia prądu I płynącego przez ten opornik oraz spadku napięcia U na nim. Wartość rezystancji wyznaczamy korzystaj*c z prawa Ohma
![]()
(6)
W przypadku pomiarów pośrednich niepewność wyznaczenia wielkości złożonej najczęściej wyznacza się metodami różniczki zupełnej lub różniczkowania logarytmicznego.
Metod* różniczki zupełnej wykorzystujemy do wyznaczania niepewności wartości wielkości „W” będącej funkcją z*o*on* zmiennych x, y oraz z mierzonych bezpośrednio:
W = f(x,y,z) (7)
Jeżeli zróżniczkujemy lewą i prawą stron* równania (7), to otrzymamy:
![]()
(8)
Jeżeli w tym ostatnim równaniu za różniczki ![]()
, ![]()
oraz ![]()
podstawimy niepewności wyznaczenia odpowiednich wielkości ![]()
, ![]()
oraz ![]()
oraz przyjmiemy, że niepewności wyznaczenia wszystkich zmiennych pomiarowych powiększają niepewność wartości wielkości złożonej „W” (czyli zastąpimy we wzorze (8) wszystkie pochodne cząstkowe ich modułami), to niepewność ![]()
wyznaczenia wielkości W można wyrazi* wzorem:
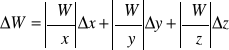
(9)
Wzór ten określa niepewność wielkości złożonej W wyznaczoną metodą różniczki zupełnej. Wartości pochodnych występujących w tym wzorze oblicza się w punktach odpowiadających najbardziej prawdopodobnym wartościom wielkości x, y oraz z, to znaczy w punktach odpowiadających wartościom średnim tych wielkości wyznaczonym na podstawie serii pomiarów.
Gdy metod* tę zastosujemy do przytoczonego przykładu wyznaczania rezystancji R wyrażonej wzorem (6), to niepewność wyznaczenia tej wielkości wyrazi się wzorem:
![]()
(10)
Metod* różniczkowania logarytmicznego stosujemy w sytuacjach, w których wielkość „W” wyznaczana na podstawie pomiarów pośrednich wielkości x, y oraz z opisana jest wzorem, w postaci:
![]()
(11)
gdzie A, a, b, c oznaczaj* pewne stałe.
Przykładem zależności funkcyjnej (11) jest wzór (6) określający rezystancję R: R=U⋅I-1.
Po zlogarytmowaniu lewej i prawej strony równania (11) otrzymujemy:
![]()
(12)
za* po zróżniczkowaniu tego ostatniego równania
![]()
(13)
Jeżeli w tym ostatnim równaniu za różniczki ![]()
, ![]()
oraz ![]()
podstawimy niepewności wyznaczenia odpowiednich wielkości ![]()
, ![]()
, ![]()
oraz przyjmiemy, że niepewności wyznaczenia wszystkich zmiennych pomiarowych powiększają niepewnoścć wielkości z*ożonej W (czyli dodamy do siebie odpowiednie moduły przyczynków pochodzących od niepewności tych wielkości , , ), to niepewność ![]()
wyznaczenia wielkości W można wyrazi* wzorem:
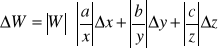
(14)
Wzór (14) określa niepewność wielkości złożonej ![]()
wyznaczoną metodą różniczkowania logarytmicznego. Gdy metod* te zastosujemy do przykładu wyznaczania rezystancji R wyrażonej wzorem (6), to niepewność wyznaczenia tej wielkości wyrazi się wzorem:
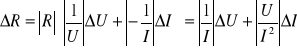
(15)
identycznym że wzorem (10), otrzymanym metodą różniczki zupełnej.
Zapis końcowego wyniku
Sposób zapisu końcowego wyniku określają normy państwowe. Zgodnie z tymi normami niepewność wyniku powinna być zapisana z dokładności* do jednej lub dwóch cyfr znaczących (za pierwszą cyfr* znacz*c* przyjmujemy cyfr* r**n* od zera, w stosunku do której po lewej stronie występuj* same zera). Z kolei liczba cyfr używanych w zapisie wartości wyniku jest ograniczona w ten sposób, iż ostatnia cyfra wyniku musi znajdować się na miejscu dziesiętnym odpowiadającym ostatniej cyfrze znaczącej w zapisie niepewności wyniku. Prawidłowo zapisanym wynikiem jest wielko**
![]()
(17)
Natomiast zapisy ( 9 * 0,01 ) [m/s2] , ( 9,810 * 1 ) [m/s2] , ( 9,810 * 0,01523 ) [m/s2],
( 9,8101 * 0,0152 ) [m/s2] są zapisami nieprawidłowymi.
Należy pamiętać, że wraz z wartości* wyniku są podawane jednostki, w których jest on wyrażony. Zawsze musimy stosować jednostki międzynarodowego układy SI lub inne jednostki dopuszczone do używania.
Sposoby przedstawiania danych eksperymentalnych
Dane eksperymentalne mogą być przedstawiane w postaci tabel, w postaci wykresów lub za pomocą odpowiednich równa* empirycznych.
Zaletami tabelarycznego przedstawiania wyników doświadczalnych są prostota konstrukcji oraz łatwość wykorzystania w przypadku dalszego matematycznego opracowywania danych. Konstruuj*c tabele należy pamięta*, iż zmienna niezależna powinna być prostą wielkości* fizyczną. Poza tym najwygodniej jest przyjmować równe odstępy 10*n , 2*10*n lub 5*10*n pomiędzy jej wartościami zawartymi w tabeli. Dane empiryczne podaje się w tabelach z dokładności* określoną przez niepewności pomiarowe.
Zaletami graficznego przedstawiania danych w postaci wykresów są: prostota sporządzania i posługiwania się wykresami reprezentującymi dane, obrazowość przedstawiania zależności funkcyjnych, pozwalaj*ca na bezpośrednie prześledzenie przebiegu funkcji, występowania maksimów i minimów, punktów przegięcia, periodyczności.
Sporządzaj*c wykres należy odpowiednio dobrać jego układ współrzędnych. Zasadniczo stosujemy dwa układy współrzędnych: kartezjański i biegunowy (tzw. wykresy ko*owe funkcji okresowych). W zależności od wyskalowania osi układu współrzędnych rozróżniamy skale równomierne (opisane równaniami ![]()
, ![]()
), skale logarytmiczne oraz skale p**logarytmiczne.
Sporządzaj*c wykresy należy pamięta*, aby zmienna niezależna by*a odkładana wzdłuż osi poziomej. Skale należy tak opisać, aby współrzędne każdego punktu można było łatwo i szybko odczyta*. W tym celu odległości między podziałkami należy wybierać równe: 10*n , 2*10*n , 4*10*n lub 5*10*n . Graniczne punkty skali należy dobierać odpowiednio do najmniejszej i największej wartości zmiennej odkładanej na danym wykresie.
Poza tym skale te należy wyrysować w takiej wielkości, aby kąt nachylenia krzywej odzwierciedlającej daną zależność funkcyjną w najbardziej interesującym nas obszarze by* zbliżony do 45o lub -45o .
Przy wykreślaniu krzywych na wykresie należy kierować się następującymi zasadami: punkty zaznacza się tylko dla przedstawienia danych liczbowych pochodzących z pomiarów, należy przy tym zaznaczać przedziały niepewności wyznaczenia tych wartości, oznaczamy je poprzez wykreślenie odpowiedniej d*ugości ramion krzyża lub poprzez zaznaczenie prostokąta o d*ugości boków odpowiadających zakresom niepewności zaznaczonego wyniku pomiaru. Krzywa ilustruj*ca na wykresie związek funkcyjny pomiędzy zmiennymi powinna być możliwie gładka. Nachylenie rożnych czę*ci tej krzywej powinno równie* zmieniać się w sposób płynny. Krzywa taka powinna przebiegać w pobliżu wszystkich punktów doświadczalnych, lecz nie musi przebiegać przez te punkty. Gdy punkty pomiarowe odbiegaj* od krzywej teoretycznej, w przybliżeniu po*owa z nich powinna leże* po jednej stronie krzywej, a druga polowa po drugiej stronie.
Aproksymacja wyników doświadczalnych
Przedstawianie wyników doświadczalnych za pomocą równania empirycznego lub równania przewidywanego teoretycznie jest najbardziej precyzyjną i wygodną metod* podawania danych. Wartości parametrów występujących w takich równaniach wyznacza się najczęściej tzw. metod* najmniejszych kwadratów (zwaną także metod* Gaussa lub metod* regresji liniowej). W metodzie tej zgodnie z postulatem Gaussa szuka się takich wartości parametr*w, przy których występuje minimum funkcji, którą oznaczamy ![]()
, kwadratów odchyle* dopasowywanej zależności teoretycznej od danych doświadczalnych
![]()
(18)
gdzie n oznacza liczbę punktów pomiarowych, Yi(xi ) - wartość dopasowywanej zależności teoretycznej wyliczona dla wartości argumentu xi, yi - zmierzona wartość zmiennej zależnej odpowiadaj*ca zmiennej niezależnej xi.
Jeżeli punkty P(x ,y ) , odpowiadające parom pomiarów x , y , wykonanym z t* sam* dokładności*, układaj* się wzdłuż pewnej prostej ![]()
, to funkcja ![]()
ma postać
![]()
. (19)
Osi*ga ona wartości minimalne gdy:
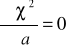
(20a)
oraz 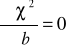
(20b)
Rozwiązuj*c układ równa* (20a) i (20b) znajdziemy następujące wzory opisujące parametry kierunkowe a oraz b prostej ![]()
, która zgodnie z postulatem Gaussa najlepiej przybliża dane wyniki pomiar*w:
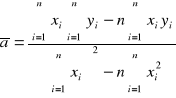
(21)
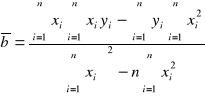
(22)
gdzie n oznacza liczbę punktów pomiarowych.
Średnie błędy kwadratowe Sa oraz Sb współczynników oraz prostej o równaniu ![]()
, wyznaczonej na podstawie wzorów (21) oraz (22), oblicza się z równa*:
(23)
(24)
przy czym:
(25)
Niekiedy nieliniową zależność funkcyjną jednej zmiennej od innej można sprowadzi* do postaci liniowej dokonuj*c odpowiedniego podstawienia przekształconych zmiennych. Przykładowo: zależność y = Aexp(Bx) (zapis ten oznacza y = A⋅eBx) można sprowadzi* do postaci liniowej η = aξ + b, przekształconych zmiennych η = lny oraz ξ = x (gdzie a = B oraz b = ln A). W konsekwencji wartości parametrów a oraz b wyznaczone metodą najmniejszych kwadratów przy użyciu powyższych wzorów pozwolą określi* wartości i niepewności wielkości A oraz B.
Przebieg ćwiczenia
Zmierzyć 10 razy za pomocą suwmiarki rozmiary wybranego ciała (prostopadłościan, walec, itp.) i za pomocą śruby mikrometrycznej średnicę np. kulki. Dla walca zmierzyć jego średnicę i wysokość.
Zanotować zakres i dokładność odczytu suwmiarki i śruby mikrometrycznej.
Dla wybranego oporu R dla 10 wartości napięcia U w zakresie 0d 2V do 25 V ustawianego na zasilaczu odczytać natężenie prądu I na zasilaczu.
Korzystając z instrukcji zasilacza zanotować sposób obliczenia niepewności pomiaru napięcia i natężenia prądu.
Opracowanie wyników
Podać definicję klasy przyrządu.
Obliczyć klasę suwmiarki i śruby mikrometrycznej.
Dla wyników uzyskanych w punkcie 1 obliczyć wartości średnie i odpowiadające im całkowite odchylenia standardowe uwzględniając dokładność suwmiarki oraz śruby mikrometrycznej. Zapisać końcowe wyniki pomiarów.
Obliczyć objętość mierzonych ciał.
Obliczyć niepewności objętości mierzonych ciał, uwzględniając obliczenia wykonane w punkcie 7, wykorzystując metodę różniczki zupełnej lub różniczkowania logarytmicznego. Zapisać końcowe wyniki.
Obliczyć niepewności natężenia prądu I i napięcia U zgodnie z punktem 4.
Sporządzić wykres zależności natężenia prądu I od napięcia U dla pomiarów przeprowadzonych w punkcie 3. Na wykresie zaznaczyć niepewności U i I.
Metodą najmniejszych kwadratów obliczyć współczynniki kierunkowe a i b prostej aproksymującej wyniki przedstawione na tym wykresie oraz niepewności wyznaczenia ich wartości. Prostą aproksymującą zaznaczyć na wykresie.
Korzystając z prawa Ohma oraz z równania prostej aproksymującej zależność I w funkcji U wyznaczyć wartość mierzonego oporu R. Zinterpretować współczynniki kierunkowe.
Obliczyć niepewność wyznaczonego w punkcie 13 oporu R metodą różniczki zupełnej lub różniczkowania logarytmicznego. Zapisać wynik końcowy.
Dla wybranej wartości napięcia i natężenia prądu obliczyć wartość oporu R korzystając z prawa Ohma oraz niepewność korzystając z obliczonych w punkcie 10 niepewności natężenia I i napięcia prądu U, metodą różniczki zupełnej lub różniczkowania logarytmicznego. Zapisać wynik końcowy.
Zestawić wyniki końcowe dotyczące obliczonych objętości badanych ciał oraz wyznaczonego oporu z aproksymacji i obliczonego z prawa Ohma.
Wnioski.
Niepewność z aproksymacji (dla średnich wartości):
![]()
![]()
![]()
![]()
=0,017 ![]()
=![]()
![]()
![]()
=0,24957
![]()
=0,167 ![]()
0,017 ![]()
-0,032 ![]()
0,251
U [V] |
I [A] |
I(z aproksymacji) [A] |
R(z prawa Ohma) [Ω] |
R(z aproksymacji) [Ω] |
2 |
0,31 |
0,302 |
6,45 |
6,622 |
4 |
0,64 |
0,636 |
6,25 |
6,289 |
6 |
0,98 |
0,97 |
6,12 |
6,186 |
10 |
1,65 |
1,638 |
6,06 |
6,105 |
12 |
1,98 |
1,972 |
6,06 |
6,085 |
14 |
2,31 |
2,306 |
6,06 |
6,071 |
16 |
2,62 |
2,64 |
6,11 |
6,061 |
18 |
2,96 |
2,974 |
6,08 |
6,052 |
20 |
3,31 |
3,308 |
6,04 |
6,046 |
25 |
4,19 |
4,143 |
5,97 |
6,034 |
|
|
Średnia: |
6,12 |
6,155 |
Wyszukiwarka