Do najczęściej wykorzystywanych miar do opisu zbiorowości statystycznej należą:
Wskaźniki struktury
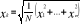
Wskaźniki natężeniaMiary opisujące tendencję centralną, czyli miary średnie
Miary dyspersji, czyli rozproszenia, zróżnicowania, rozrzutu
Miary asymetrii
Miary koncentracji
![]()
Wskaźnik struktury - mówi jaki jest udział wyróżnionej zbiorowości w całej zbiorowości
ni -liczba jednostek charakteryzujących się i-tym wariantem,
wartością cechy.
N-liczba jednostek zbiorowości
![]()
Inaczej wskaźnik struktury nazywa się odsetkiem, frakcją, procentem.
![]()
Do porównania rozkładu tej samej cechy w dwóch różnych zbiorowościach statystycznych stosuje się wskaźnik podobieństwa struktur.
Im wskaźnik Wp bliższy jest jedności tym bardziej podobne do siebie są rozkłady cech w tych zbiorowościach.
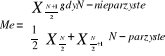
Klasyczne miary średnie: średnia arytmetyczna, harmoniczna, geometryczna i kwadratowa.
Średnia arytmetyczna jest to suma wartości cechy mierzalnej dla wszystkich jednostek statystycznych podzielna przez liczbę.
![]()
![]()
![]()
W przypadku szeregów rozdzielczych z przedziałami klasowymi umownym reprezentantem każdego przedziału jest środek tego przedziału. W związku z tym średnia arytmetyczna może być nieco zniekształcona.
Własności średniej arytmetycznej:
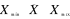
Średnia arytmetyczna jest wypadkową wszystkich wartości badanej cechy w związku z tym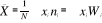
![]()
![]()
![]()

Suma kwadratów odchyleń poszczególnych wartości badanej cechy od średniej arytmetycznej jest najmniejsza. Oznacza to, że średnia arytmetyczna jest najlepszą miarą średnią pod wieloma względami.
Średnia arytmetyczna ma również wady:
Jest bardzo wrażliwa na wartości nietypowe cechy, gdy takie wartości występują w szeregu to średniej arytmetycznej nie należy liczyć.
Przez obserwację nietypową rozumiemy obserwację skrajną, ale występującą w niewielkiej ilości mniej niż 10%.
Średniej arytmetycznej nie liczymy również gdy skrajne przedziały klasowe są otwarte, chyba że można je w sensowny sposób domknąć.
![]()
Średnią geometryczną liczymy wtedy gdy w szeregu występują znaczne różnice między obserwacjami.
![]()
Często stosuje się postać logarytmiczną.
Własności średniej geometrycznej:
Srednia geometryczna wychodzi równa zero gdy jedna z obserwacji jest równa zero.
Średnia geometryczna może być wartością urojoną gdy choć jedna z obserwacji jest wartością ujemną.
Stosujemy ją gdy wartości wyrażają zmiany stosunkowe.
![]()
Średnia harmoniczna - stosujemy ją dla wielkości stosunkowych.
Przykład :
Samochód z miasta A do B jechał z prędkością 50km/h natomiast z miasta B do C 70km/h jeżeli odległość między tymi miastami jest równa średnią prędkość na tej trasie należy liczyć jako średnią harmoniczną i otrzymamy taką samą wartość jak wtedy gdybyśmy przejechaną odległość na całej trasie podzielili przez czas przejazdu na całej trasie.
Średnia kwadratowa
Używana jest rzadko np. stosujemy ją we wzorze na odchylenia standardowe.
Średnie klasyczne charakteryzują się tym, że obliczane są ze wszystkich wartości cechy.
![]()
Średnie miary pozycyjne:
Mediana (wartość topologiczna) - to wartość jednostki statystycznej położonej w zbiorowości w ten sposób, że liczba jednostek mających wartość niemniejszą od mediany równa jest liczbie jednostek mających wartość niewiększą od mediany.
Własności mediany:
Nie zależy ona od wartości krańcowych.
Można ją wyznaczyć gdy wszystkie liczebności nie są dokładnie znane, wystarczy znać liczebność zbiorowości i jednostkę środkową.
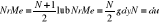
Medianę można policzyć wtedy gdy nie można obliczyć średniej arytmetycznej. Medianę można policzyć na skali porządkowej (wtedy nie można obliczyć średniej arytmetycznej, harmonicznej, ani geometrycznej)
W szeregu rozdzielczym z przedziałami klasowymi:
![]()
Jest to wzór interpolacyjny wyprowadzony przy założeniu, że przedziale mediany cecha zachowuje się w sposób liniowy.
Najprostsza skala nazywa się skalą nominalną, np. ktoś jest protestantem, a ktoś katolikiem (nie wiemy kto jest lepszy).
Następna jest skala porządkowa, czyli jakaś hierarchia, np. wykształcenie wyższe jest lepsze niż średnie, a średnie lepsze niż zawodowe.
Skala interwałowa - możemy na niej liczyć odległości między wartościami, ale nie posiada ona zera bezwzględnego.
Skala ilorazowa - posiada odległości i ma zero bezwzględne.
Następnymi miarami pozycyjnymi są kwartyle:
Kwartyl pierwszy jest równy wartości cechy takiej, że ¼ zbiorowości ma wartości nie przekraczające tej cechy, a ¾ zbiorowości ma wartości niemniejsze od tej cechy.
Kwartyl trzeci analogicznie, tzn. jest to taka wartość cechy, że ¾ zbiorowości ma wartości nie przekraczające tej cechy.
Mediana jest drugim kwartylem.
![]()
Dominanta zwana wartością najczęstszą (zwana modą, wartością modalną, typową).
Dominanta jest to ta wartość cechy, która występuje w zbiorowości statystycznej najczęściej.
W szeregu szczegółowym obliczamy ją z definicji, natomiast w szeregu rozdzielczym z przedziałami klasowymi z następującego wzoru:
![]()
Wzór ten stosujemy gdy jest jeden przedział dominujący; rozpiętości przedziału dominanty poprzedniego oraz następnego są równe.
Własności dominanty:
Rozkład cechy musi posiadać jedną wyraźnie zaznaczoną wartość dominującą w przeciwnym razie mówimy o szeregach wielo modalnych. Szereg nie może być skrajnie asymetryczny z otwartym przedziałem dominującym (nie można wtedy w ogóle obliczać dominanty).
Miary dyspersji i asymetrii:
Dyspersja - to inaczej rozproszenie, zróżnicowanie, rozrzut, zmienność.
Przykład ilustrujący potrzebę stosowania miar dyspersji:
Rozważmy 2 grupy 10-cio osobowe o następujących wartościach wieku:
16,18,19,19,20,20,21,21,23,23
4,6,8,10,19,20,29,30,40,42
w obydwu grupach średnia wieku jest w przybliżeniu równa 20 lat, lecz obydwie grupy różnią się rozkładem wieku bardzo istotnie.
Miary zróżnicowania służą do tego by ocenić w jakim stopniu poszczególne wartości cechy koncentrują się wokół wartości średniej (jakie jest zróżnicowanie cechy w danej zbiorowości).
Miary dyspersji informują jak duże jest odchylenie pomiędzy poszczególnymi wartościami cechy, a wartością przeciętną.
Klasyczne miary dyspersji to:
odchylenie przeciętne,
wariomcja,
odchylenie standardowe.
Przydatne wzory i ich interpretacja:
ŚREDNIA ARYTMETYCZNA - przeciętnie każde z (jedn. Stat.) ma ......
![]()
![]()
numer mediany
![]()
MEDIANA - połowa (nazwa zbiorow.) ma (cecha stat.) nieprzekraczającą ....., a połowa niemniejszą
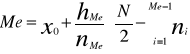
KWARTYL PIERWSZY - jedna czwarta (nazwa zbior.) ma (cecha) niewiększą niż….., a ¾ niemniejszą
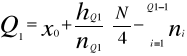
KWARTYL TRZECI - tak samo jak pierwszy
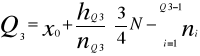
ODCHYLENIE ĆWIARTKOWE - (cecha) (jednostka) odchyla się średnio od mediany o …, czyli o … tej średniej
![]()
![]()
![]()
DOMINANTA - dominują (jednostki) o (cecha) …
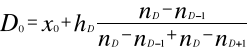
ODCHYLENIE STANDARDOWE - (cecha) (jednostka) odchyla się średnio od średniej arytmetycznej średnio o …, czyli o …tej średniej
![]()
![]()
WSPÓŁCZYNNIK SKOŚNOŚCI - ile jednostek (większość, mniejszość) ma wartość cechy mniejszą (większą) od średniej arytmetycznej.
![]()
ASYMETRIA - jaki rodzaj asymetrii wskazuje >0 - prawostronna ; <0 - lewostronna
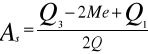
![]()
Statystyka - nauka zajmująca się badaniem prawidłowości zjawisk ( procesów) masowych przy pomocy metod ilościowych. Przez badania statystyczne rozumiemy poznanie struktury określonej zbiorowości statystycznej.
Zbiorowość generalna, zbiorowość próbna.
Zbiorowość statystyczna - nazywamy zbiór dowolnych elementów (przedmiotów i faktów) podobnych pod względem określonych cech (ale nie identycznych) i poddanych badaniom statystycznym.
Bezpośrednie obserwacji lub pomiarowi podlegają elementy składowe zbiorowości (obiekty badane) zwane jednostkami statystycznymi.
Zbiorowość próbna (próba) jest to podzbiór populacji generalnej. Próba podlega badaniu statystycznemu, a wnioski badania są uogólnione na całą zbiorowość generalną.
Liczbę elementów próby oznaczamy przez n. Próba jest mała albo n≤30 duża dla n>30
Aby uzyskane wyniki badań próby można odnieść do zbiorowości generalnej musi być reprezentatywna. Próba wybrana w sposób losowy i dostatecznie duża nazywa się reprezentatywna. Jej struktura jest podana do struktury generacji.
Rodzaje badania statystycznego.
Całkowite (wyczerpujące) - gdy obserwacji podlegają wszystkie elementy zbiorowości generalnej.
Częściowe - gdy obserwacji podlega część zbiorowości generalnej.
Rodzaje badań częściowych:
badania reprezentatywne
badania monograficzne
badania ankietowe
ad 1. w sposób losowy wybieramy próbę i na postawie jej badań wnioskujemy o całości (zbiorowości generalnej). Metoda ta polega na szacowaniu nieznanych parametrów zbiorowości generalnej na podstawie wyników uzyskanych z badania próbki
ad 2. badany jest pojedynczy przypadek np. jedna wieś czy gmina
ad 3. nie badamy zbiorowości statystycznej bezpośrednio lecz zwracamy się do różnych instytucji lub osób z prośbą o wypełnienie odpowiedniej ankiety.
Badanie statystyczne - mogą być obarczone błędami.
Błędy statystyczne - popełnione celowo lub w skutek awarii urządzenia. Są one groźne mogą zniekształcić badania.
Błędy przypadkowe - w trakcie badania nie mają większego wpływu na wynik
Jednostki statystyczne charakteryzują się pewnymi właściwościami, które nazywamy cechami statystycznymi.
Rodzaje cech:
cechy niemierzalne (jakościowe) - są one określone słownie, np.: płeć, rozmieszczenie terytorialne
cechy mierzalne (ilościowe) - są to właściwości, które można zmierzyć i wyrazić za pomocą liczby
Cechy mierzalne będziemy nazywać zmiennymi losowymi i oznaczymy przez x, y, z, a wartości cech przez xi, yi, zi
Zmienne losowe dzielimy na :
skokowe (dyskretne) przyjmują one skończony lub przeliczalny zbiór wartości np..: liczba osób w rodzinie, liczba usterek itp.
ciągłe - mogą przyjąć każdą wartość z określonego przedziału liczbowego [a,b]
Opracowanie i prezentacja materiału statystycznego.
Zebrany surowy materiał statystyczny nie nadaje się jeszcze do dalszych badań, należy go najpierw odpowiednio pogrupować. Grupowanie to polega na podziale niejednakowych zbiorowości na możliwie jednorodne grupy pod względem pewnych ustalonych kryteriów. Zależy ono oczywiście od celu badania, a także od charakteru wybranych cech.
Ze względu na badanie grupowe dzielimy na:
typologiczne
wariancyjne
analityczne
Po sklasyfikowaniu danych statystycznych według jakiegoś kryterium otrzymujemy szereg statystyczny.
Szeregi statystyczne dzielimy na:
szczegółowe
rozdzielcze
czasowe
Szczegółowe - najczęściej stosowany jest wtedy, gdy liczba jednostek objętych badaniem jest mała (10, 20 osób)
Rozdzielcze - stanowi zbiorowość statystyczną podzieloną na klasy wg określonej cechy jakościowej lub ilościowej z podaniem liczebności każdej z klas. Szeregi rozdzielcze dzielimy na: punktowe i przedziałowe.
Punktowy szereg rozdzielczy - buduje się wówczas, gdy liczba wariantów badanej cechy niewielka, a każdy z tych wariantów występuje kilka razy w badanej zbiorowości.
Szereg rozdzielczy przedziałowy - stanowi zbiorowość statystyczną podzieloną na klasy wg określonej cechy jakościowej lub ilościowej z podaniem liczebności każdej z klas.
W szeregach rozdzielczych do określenia struktury badanej zbiorowości stosuje się wskaźnik struktury (częstość, liczebność względna czy odsetki) 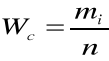
mi - iloczyn sprzyjających cech
n - ilość wszystkich możliwych cech
przy czym 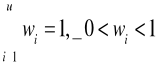
Skumulowany wskaźnik struktury
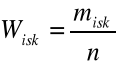
i=1,2, ..... k
Do szeregów statystycznych zaliczamy również szeregi czasowe.
Rodzaje szeregów czasowych:
szeregi czasowe okresów - ujmuje zjawiska w tygodniu, miesiącu, roku
szeregi czasowe momentów - ujmują wielkość zjawiska w danym momencie
Konstrukcja szeregu rozdzielczego z przedziałami klasowymi.
określenie empirycznego obszaru zmienności (rozstępu) cechy
ustalenie liczby przedziałów klasowych (k) i ich długości (h) najczęściej wg wzoru:
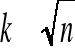
zaś
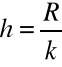
Uwaga!!! Istotne jest ustalenie granic poszczególnych klas.
Prezentacja pierwszej klasy. Jej granice dolne to z reguły minimalna wartość liczby lub cechy.
Prezentacja graficzna szeregów statystycznych.
Najczęściej stosuje się wykresy:
liniowe (diagramy i krzywe liczebności)
powierzchniowe
słupkowe
Miary tendencji centralnej:
Są najczęściej rozpowszechnionymi miarami statystycznymi używanymi w praktyce. Podają one pomocą jednej liczby charakterystykę poziomu wartości zmiennej czyli tendencję centralną (stąd nazwa miary tendencji centralnej)
Miary te dzielimy na:
przeciętne miary klasyczne (średnia arytmetyczna, średnia geometryczna, średnia harmoniczna)
przeciętne miary pozycyjne (dominanta i kwestyle) wśród których szczególnie wyróżniamy kwastyl drugi tzn. medianę
miary zmienności (rozproszenia i dyspersji)
miary asymetrii
miary koncentracji
Średnia arytmetyczna jest sumą wartości cechy mierzalnej podzieloną przez liczbę jednostek skończonej zbiorowości statystycznej tzn.: 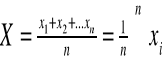
Jest to średnia arytmetyczna nieważna (prosta). Jest wykorzystana dla szeregów indywidualnych dla szeregu rozdzielczego punktowego
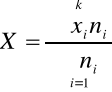
gdzie: k - liczba klas
ni -liczebność poszczególnych klas
Dla szeregu rozdzielczego z przedziałami klasowymi
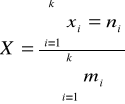
Xi - środek przedziału klasowego
Jeżeli w miejsce względne (ni) podstawimy wskaźnik struktury to średnia arytmetyczna ważona przyjmuje postać. 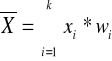
lub 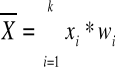
Własności:
średnia arytmetyczna jest wypadkową wszystkich wartości zmiennych i spełnia warunek:
![]()
Xmin < ![]()
< Xmax
Suma odchyleń poszczególnych wartości zmiennej (cechy) od średniej jest równa zeru.
![]()
lub ![]()
Suma kwadratów odchyleń poszczególnych wartości cechy (zmiennej) od średniej jest minimalna.
![]()
lub ![]()
Średnią arytmetyczną oblicza się w zasadzie dla szeregów o zamkniętych przedziałach klasowych.
Średnia arytmetyczna jest wrażliwa na skrajne wartości cechy są to tzw. Obserwacje przypadkowe.
Średniej arytmetycznej nie powinno się obliczać, gdy w szeregu występują nietypowe wartości.
Jeżeli znamy średnią arytmetyczną dla pewnych n- grup i chcemy wyznaczyć średnią arytmetyczną dla wszystkich grup łącznie, wówczas:
gdzie:
![]()
- arytm. Dla wszystkich grup łącznie
xi - średnia arytmetyczna w i-tej grupie
ni - liczebność tej grupy
n - suma liczebności we wszystkich grupach 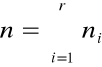
Średnia harmoniczna - jest to odwrotność średniej arytmetycznej
Odwrotności liczb dla szeregu szczegółowego:
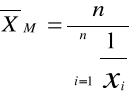
dla szeregu indywidualnego
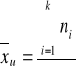
Przykład:
W ciągu 8 godzin obserwowano parę 5 robotników. Robotnik A zużył na wykonanie 1 elementu 4min, B- 6min., C- 12min. Obliczyć ile czasu zużyją średnio ci robotnicy na wykonanie 1 elementu.
Średnia geometryczna - określa się wg wzoru:
gdzie:
x1 - indywidualny indeks łańcuchowy
n - liczba tych indeksów
Średnią arytmetyczną stosuje się wtedy, gdy zjawiska są ujmowane dynamicznie
Dominanta (wartość najczęstsza, modalna) oznaczamy ją symbolem Mo lub b - jest to wartość cechy, która występuje najczęściej w badanej zbiorowości. Do szeregów rozdzielczych z przedziałami klasowymi przybliżoną wartość modalnej wyznacza się ze wzoru lub graficznie z histogramu liczebności interpolacyjnego. Analitycznie modalną wyznacza się ze wzoru:
gdzie:
xm - dolna granica przedziału w którym występuje modalne (dominanta)
nm - liczebność przedziału w którym występuje modalna
nm-1 - liczebność klasy poprzedzającej przedział modalny
nm+1 - liczebność klasy następnej w przedziale modalnej
hn - rozpiętość przedziału klasowego, w którym występuje modalna
Dominantę obliczamy gdy:
przedziały klasowe są równej długości, a przynajmniej jednakowej długości jest przedział dominanty oraz przedział poprzedzający i następujący po przedziale dominanty
nie wyznacza się dominanty w przypadki, gdy największa liczebność jest w pierwszym lub ostatnim przedziale klasowym oraz gdy rozkład empiryczny ma więcej niż jeden ośrodek dominujący
wartość dominanty nie zmienia się, gdy zamiast liczebności do wzoru wstawimy częstość (wskaźnik struktury)
Kwartyle - są to wartości cechy badanej zbiorowości przedstawionej w postaci szeregu statystycznego, które dzielą zbiorowość na określone części pod względem liczby jednostek. Części te pozostają w stosunku do siebie w określonych proporcjach.
Szeregi, w których wyznacza się kwartyle muszą być uporządkowane w ciąg monotoniczny (rosnący lub malejący). Do najczęściej stosowanych kwartyli należą: kwartyle, decyle, centyle.
KWARTYLE
Kwartyl pierwszy a1 - dzieli zbiorowość uporządkowaną na dwie części w ten sposób, że 25% jednostek zbiorowości ma wartość cechy nie większą niż a1, a 75% nie mniejszą od tego kwartyla.
Kwartyl drugi (mediana Me) - dzieli zbiorowość uporządkowaną na dwie równe części. Połowa jednostek ma wartości cechy mniejsze lub równe medianie, a połowa wartości cechy równe lub większe od mediany.
Kwartyl trzeci a3 - dzieli zbiorowość na dwie części w ten sposób, że 75% jednostek ma wartość cechy nie wyższe, a 25% nie niższe niż kwartyl trzeci.
Prezentowane dotychczas metody statystyczne dotyczyły analiz struktury zbiorowości ze względu na jedną cechę (zmienną).
Obecnie zajmiemy się badaniem zbiorowości, która charakteryzowana jest za pomocą więcej niż jednej zmiennej (cechy) i zmienne te wzajemnie się warunkują.
Celem takiego badania jest stwierdzenie, czy między badanymi zmiennymi zachodzą określone zależności, czy są to zależności prostoliniowe czy krzywoliniowe, jaka jest ich siła, kształt i kierunek.
Współzależności między zmiennymi może być:
funkcyjna - gdy określonej wartości zmiennej X odpowiada dokładnie jedna i tylko jedna wartość zmiennej X
statystyczna (probalistyczna) - jest to zależność między dwiema zmiennymi losowymi polegająca na tym że wraz ze zmianą jednej zmiennej, zmienia się rozkład prawdopodobieństwa drugiej zmiennej.
Zależność statystyczna (korelacyjna) jest szczególnym przypadkiem zależności stochastycznej.
W zależności korelacyjnej określonym wartością jednej zmiennej są przypadkowe pewne średnie wartości drugiej zmiennej.
Metody badania współzależności
Dana jest populacja generalna, w której interesują nas cechy mierzalne (x, y) traktowane jako zmienne losowe.
Jeżeli są nieznane pewne parametry rozkładu dwuwymiarowej zmiennej.
Jeżeli są nieznane pewne parametry rozkładu dwuwymiarowej zmiennej losowej (x, y) to powstaje problem wyznaczenia ich oszacowań.
Podobnie jak przy badaniu ze względu na jedną cechę oszacowania te wyznacza się z prób.
Przy badaniu ze względu na dwie cechy próbkę stanowi n par (x, y), i=1, ...n których pierwsza jest zaobserwowaną wartością cechy x, druga zaś cechy y.
Traktując (x, y) jako współrzędne punktu na płaszczyźnie można próbką przedstawić graficznie w postaci tzw. Diagramu korelacyjnego.
Korelacja liniowa dodatnia Korelacja liniowa ujemna
Korelacja krzywoliniowa Brak korelacji
Dla dużych próbek w celu stwierdzenia istnienia lub braku związku korelacyjnego buduje się tablicę korelacyjną.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Nij - liczba obserwacji (jednostek), które posiadają jednocześnie wariant xi cechy x i wariant yi cechy y.
N - liczebność próby,
Ni, Nj - rozkłady szeregowe odpowiednio zmiennej x oraz y
Przykład brzegowy zmiennej x tworzy pierwsza i ostatnia kolumna tabeli, rozkład brzegowy zmiennej y pierwszy i ostatni wiersz.
Zmienna losowa x przyjmuje K wariantów (i=1, ....k)
Zmienna losowa y przyjmuje L wariantów (i=1, ....l)
Symbol nj oznacza liczbę jednostek, które mają wariant yi zmiennej y, natomiast ni - liczbę jednostek, które mają wariant xi zmiennej x.
W tablicy korelacyjnej oprócz rozkładów brzegowych zmiennej (x, y) są rozkłady warunkowe. Rozkład warunkowy przedstawia strukturę wartości jednej zmiennej (x lub y) pod warunkiem, że druga zmienna przyjęła określoną wartość.
Rozkład warunkowy zmiennej x zapisujemy x\y = yj
Rozkład warunkowy zmiennej y zapisujemy y\x = xi
Średnie arytmetyczne z rozkładów brzegowych
Średnie arytmetyczne rozkładów warunkowych
Na podstawie tablicy korelacyjnej można stwierdzić, czy związek między zmiennymi x i y jest liniowy.
Związek jest liniowy, jeżeli różnice między średnimi warunkowymi danej zmiennej obliczonymi dla konkretnych wariantów drugiej zmiennej są takie same tzn.
Siłę, kierunek i kształt związku korelacyjnego można stwierdzić na postawie oceny stopnia skupienia lub rozproszenia liczebności nij tablicy korelacyjnej gdy warianty zmiennych x i y ułożone są w tablicy rosnąco, to skupianie się liczebności wzdłuż przekątnej biegnącej od lewego górnego do prawego dolnego rogu tablicy świadczy o istnieniu korelacji dodatniej i prostoliniowej.
Odwrotny układ liczebności (od prawego górnego do lewego dolnego rogu tabeli), świadczy o istnieniu korelacji ujemnej prostoliniowej.
Skupienie się liczebności w tablicy korelacyjnej w innym charakterystyczny sposób (kształt paraboli, funkcji wykładniczej) może świadczyć o istnieniu korelacji krzywoliniowej.
Gdy zaś liczebności rozrzucone są chaotycznie po całym polu tablicy, to między zmiennymi nie ma zależności korelacyjnej
Charakter i siłę zależności korelacyjnej możemy wyrazić:
Obliczając odpowiednie miary ścisłości związku korelacyjnego.
Wyznaczając funkcje regresji.
Badanie ścisłości związku korelacyjnego.
Siłę zależności dwóch zmiennych można wyrazić liczbowo, stosując odpowiednie mierniki np.:
10 wskaźnik korelacyjny Pearsona (stosunek korelacji)
20 współczynnik korelacji liniowej Pearsona
30 współczynnik korelacji rang Spearmana
Ad 10 wskaźnik korelacyjny Pearsona zmiennej y względem x ma postać (y - zmienna zależna)
Wskaźnik korelacyjny Pearsona zmiennej v względem y (x - zmienna zależna)
S(x) i S(y) - odchylenie standardowe zmiennych x i y
Natomiast odchylenia standardowe średnich grupowych czyli warunkowych wyrażają się wzorem:
Gdzie:
, - są średnimi warunkowymi zmiennymi x i y (obliczanymi na podstawie tablicy korelacyjnej)
, - są średnimi ogólnymi obliczonymi dla odpowiednich zmiennych, przy wykorzystaniu rozkładów brzegowych.
Wskaźniki eyx i exy przyjmują wartość z przedziału [0,1] (1e) gdy są równe zero - cechy są nieskorelowane .
Ad 20 gdy są równe 1 zachodzi między nimi zależność funkcyjna.
Na ogół exy ≠ eyx z wyjątkiem przypadków 10 i 20
Współczynnik korelacji liniowej Pearsona.
-1<rxy<1
Kowariancja (w u (x, y)) jest średnią arytmetyczną iloczynu odchyleń poszczególnych zmiennych od ich średnich arytmetycznych.
w u (x, y)=0 brak zależności korelacyjnej,
w u (x, y)<0 ujemna zależności korelacyjnej,
w u (x, y)>0 dodatnia zależności korelacyjnej.
Współczynnik korelacji liniowej jest to średnia geometryczna dwóch współczynników regresji liniowej
Współczynnik korelacji rxy przyjmuje zawsze taki sam znak jaki mają współczynniki regresji.
Współczynniki regresji a1, b1 mają zawsze jednakowe znaki:
albo obydwa dodatnie
albo obydwa ujemne
Przyjmuje się, że korelacje między dwoma cechami jest:
Nie wyrażona, gdy (r) ≤ 0,3
Średnie, gdy 0,3 < (r) < 0,5
Wyraźna, gdy (r) ≥ 0,5
Zachodzi zależność funkcyjna, gdy (r) = 1(korelacja doskonała)
Współczynnik korelacji rang Spearmana.
Obliczenia rozpoczynamy od uporządkowania wyjściowych informacji według rosnących (malejących) wariantów jednej z cech. Tak uporządkowanym wartościom nadajemy numery kolejnych liczb naturalnych. Czynności te nazywa się rangowaniem.
Di - różnice między rangami odpowiadających sobie wartości cechy xi, yi (i=1, ...n)
N - liczba obserwacji
Liniowa funkcja regresji.
Przez analizę regresji rozumiemy metodę badania wpływu zmiennych uznanych za objaśniające (niezależne) na zmianę uznaną za objaśnioną (zależną).
Model zależności stochestycznej.
Y f(x, ) (1)
y- zmienna zależności (objaśniona)
x - zmienna niezależna (objaśniająca)
q - składnik losowy (błąd) określający odchylenia przypadkowe wartości zmiennej y od wartości funkcji regresji.
Nadrzędnym badaniem zależności (1) jest:
funkcje regresji = (x) (2) która konkretnym wartościom zmiennej niezależnej przyporządkowuje warunkowe średnie zmiennej zależnej.
Funkcje regresji zmiennej y względem zmiennej x
E((y)x=xi)= (xi); i=1,...n (3)
funkcje regresji zmiennej x względem zmiennej y
E (x) y=yi i=1, ... n
Gdzie:
X1Y1 - to kolejne obserwacje zmiennej x i y.
Graficznym obrazem funkcji (xi) i 2(yi) są linie łamane, zwane empirycznymi liniami regresji. Funkcje 1(x1) i 2(yi) mogą być dowolnego typu tzn. mogą mieć kształt liniowy, potęgowy i wykładniczy, wielomianowy.
W badaniach praktycznych najczęściej wykorzystuje się liniowe funkcje regresji y1= (x)
Regresje zmiennej y względem zmiennej x I rodzaju
Gdzie:
Y1 - teoretyczne wartości funkcji regresji y1= (x)
0 1 - parametry strukturalne liniowej funkcji regresji y względem x
- składnik losowy (błąd) jest zmienną losową oraz
Analogicznie regresjie zmiennej x względem zmiennej y ma postać również pierwszego rodzaju.
Parametry strukturalne modelu nieznane i mogą być oszacowane na podstawie wyników badania (zaobserwowanych wartości zmiennej x oraz y). Metoda które daje dobre oszacowanie tych parametrów jest metoda najmniejszych kwadratów (MNK). Daje ona najlepsze liniowe nieobciążone estymatory parametrów regresji o możliwie najmniejszej
Erystomery najmniejszych kwadratów:
A0, B0 - szacuje 0, 0
A1, B1 - szacuje 1, 1
Oszacowanym równaniem regresji jest:
Y1=a0+a1x
Lub
X1=b0+b1y
Gdzie:
X1,y1 - są to wartości teoretyczne zmiennych x oraz y
A0, b0, a1, b1 - są ocenami nieznanych parametrów 0, 1, 0, 1
Różnice między wartościami empirycznymi y i a teoretycznymi y11 nazywamy resztami i oznaczamy:
Na czym polega metoda najmniejszych kwadratów:
Zatem szacowanie nieznanych parametrów sprowadza się do znalezienia takiej linii prostej aby:
odchylenie wartości empirycznych od teoretycznych miały charakter losowy tzn.: były statystycznie nieistotne.
Suma kwadratów tych odchyleń (reszt) była minimalna.
Miary przeciętne
Medianę w szeregach uporządkowanych wyznacza się ze wzoru:
Przykład:
Dwóch pracowników wykonuje metale tego samego typu. Przeprowadzono obserwację czasu wykonywania gięcia metali przez robotnika a i dziesięć metali przez robotnika b i otrzymano następujące szeregi szczegółowe opisujące czas wykonania metali (w minutach).
Dla robotnika a: 12,15, 15, 18, 20, 21, 21 Robotnik a zużył 80 min. Na wykonanie 5 metali. Robotnik b zużył 154 minut na wykonanie 10 metali. Znaleźć średni czas wykonania jednego metalu przez robotnika a. Średni czas wykonania jednego metalu przez robotnika b, oraz Me, Q1, Q3.
Rozwiązanie:
W szeregach rozdzielczych przedzielonych medianą wyznacza się ze wzoru:
Gdzie:
M - numer przedziału (klasy) w którym występuje mediana
Xm - dolna granica przedziału, w którym występuje mediana
suma liczebności przedziałów poprzedzających przedział mediany czyli liczebności skumulowana rozpiętość.
Hm - rozpiętość przedziału klasowego, którym jest mediana
nme - pozycja mediany
Pozycje mediany - (jednostki środkowej) ustala się na poziomie połowy liczebności próby:
Sposób wyznaczania kwartyli Q1 i Q3
Dla szeregów szczególnych - kwartyle Q1 i Q3 wyznacza się tak jak mediane. W szeregach rozdzielczych wyznaczenie kwartyli poprzedza ustalenie ih pozycji według wzoru:
Dla szeregów rozdzielczych z przedziałami klasowymi stosujemy wzory:
Gdzie:
M - numer przedziału, w którym występuje odpowiadający mu kwartyl.
Xm - dolna granica przedziału.
N - liczebność przedziału, w którym występuje dolny kwartyl.
liczebność skumulowana do przedziału poprzedzającego kwartyl.
M - rozpiętość przedziału, w którym występuje dany kwartyl.
Miary zmienności.
Miary zmienności (rozproszenia, dyspersja) charakteryzują stopień zróżnicowania jednostek zbiorowości pod względem badanej cechy. Podobnie jak miary przeciętne, określamy je na klasyczne i pozycyjne.
Do miar zmienności klasycznych zaliczamy.
odchylenia standardowe
warjancje
odchylenie przeciętne
Do miar zmienności pozycyjnych zaliczamy:
rozstęp
odchylenie ćwiartkowe
współczynnik zmienności
Uwaga!!!
Współczynnik zmienności w zależności od techniki obliczania może być miarą dyspersji klasyczną lub pozycyjną.
Warjancja, odchylenie standardowe, odchylenie przeciętne.
Warjancja - to średnia arytmetyczna kwadratów odchyleń poszczególnych wartości cechy od średniej arytmetycznej zbiorowości.
Dla szeregów szczegółowego warjancję wyznacza się wg wzoru.
Dla szeregu rozdzielczego punktowego:
Dla szeregu rozdzielczego z przedziałami klasowymi:
Własności warjancji:
warjancja jest różnicą między średnią arytmetyczną kwadratów wartości zmiennej, a kwadratem średniej arytmetycznej tej zmiennej, czyli:
jeżeli badaną zbiorowość podzielimy na k grupy (wg określonego kryterium) to warjancja dla całej zbiorowości (warjancja ogólna), będzie sumą dwóch wskaźników i średniej arytmetycznej wewnątrz grupowych warjancji wartości zmiennej, warjancji wewnątrz grupowej oraz warjancjj średnich grupowych wartości tej zmiennej
gdzie:
k - liczba grup na jaką podzielono badaną populacje
n - liczebność zbiorowości
Si2 - średnia arytmetyczna ważona z warjancją wewnątrz grupowych
- średnia arytmetyczna całej populacji
- średnia arytmetyczna i - tej grupy
- warjancje średnich grupowych (warjancje między grupowe)
warjancja jest zawsze wielkością nieujemną i mianowaną
im zbiorowość jest bardziej zróżnicowana tym wyższa jest wartość warjancji
Odchylenie standardowe - jest pierwiastkiem kwadratowym z warjancji.
Parametr ten określa przeciętne zróżnicowanie poszczególnych wartości cechy od średniej arytmetycznej.
Typowy obszar zmienności określa wzór:
W obszarze tym mieści się około 2/3 wszystkich jednostek badanej zbiorowości statystycznej.
Odchylenie przeciętne - jest średnią arytmetyczną bezwzględnych wartości odchyleń poszczególnych wartości zbiorowości statystycznej od średniej arytmetycznej.
Dla szeregu szczegółowego
Dla szeregu rozdzielczego punktowego
Dla szeregu rozdzielczego przedziałowego
najprostszą miarą dyspersji jest empiryczny obszar zmienności (rozstęp).
R = xmax - xmin
odchylenie ćwiartkowe
Mierzymy poziom zróżnicowania tylko części jednostek badanej zbiorowości tzn. po odrzuceniu 25% jednostek o wartościach najmniejszych i 25% jednostek o wartościach największych. Odchylenie to mierzymy więc średnią rozpiętości w połowie obszaru zmienności.
Typowy obszar zmienności (w zależności od mediany)
Współczynnik zmienności
Lub przy wykorzystywaniu miar pozycyjnych
Współczynnik zmienności jest wielkością nie uwarunkowaną przyjmuje się, że jeżeli współczynnik zmienności jest < 10% to cechy wykazują małe zróżnicowanie. Współczynnik zmienności stosuje się wtedy, gdy chcemy porównać kilka zbiorowości pod względem tej samej cechy lub tej samej zbiorowości pod względem kilku różnych cech.
Miary asymetrii
W wielu sytuacjach badanie średniego poziomu cechy i rozproszenia jej wartości nie wystarcza do analizy zbiorowości. Istotne jest jeszcze stwierdzeniem, czy większość badanych jednostek ma wartość cechy powyżej czy poniżej przeciętnego poziomu. Problem ten wiąże się z oceną asymetrii (skośności) rozkładu.
Asymetrię najładniej jest określić następująco:
asymetria prawostronna
lub asymetria lewostronna
Miarą określającą kierunek i siłę asymetrii jest współczynnik asymetrii (miara niemianowana). Współczynnik ten w zależności od miar klasycznych czy pozycyjnych wyraża się wzorem:
Wartość współczynnika -1<As<1- przy bardzo silnej asymetrii może przekroczyć nieznacznie ±1
Dla rozkładu umiarkowanie asymetrycznego zachodzi związek:
Miary koncentracji - statystyczny opis struktury zjawisk masowych można również przeprowadzić pod względem badania siły koncentracji.
Rozróżnia się dwa rodzaje koncentracji
jako koncentrację zbiorowości wokół średniej
jako nierównomierny podział ogólnej sumy wartości cechy (tzw. Łącznego funduszu cechy) między poszczególnymi jednostkami zbiorowości.
Miarą skupienia obserwacji wokół średniej jest współczynnik skupienia (kurioza).
Przy czym:
Im wyższa wartość współczynnika k, tym większa koncentracja wartości cechy wokół średniej gdy:
k=3 - rozkład normalny
k>3 - rozkład jest wysmukły
k<3 - rozkład spłaszczony
Współczynnik ekscesu.
Informuje, czy koncentracja wartości zmiennej wokół średniej w danym rozkładzie jest większa czy też mniejsza w zbiorowości o rozkładzie normalnym.
Ze zjawiskiem koncentracji drugiego rodzaju mamy do czynienia wówczas, gdy występuje nierównomierny podział łącznego funduszu cechy (np. dochodu, produkcji) pomiędzy poszczególne jednostki zbiorowości (np. indywidualne osoby, zakłady produkcyjne) itp.
Koncentracja - jest tu związana z asymetrią i dyspersją im większa asymetria i zróżnicowanie jednostek tym większa jest koncentracja.
Dwa skrajne przypadki: to brak koncentracji oraz koncentracja zupełna
gdy brak koncentracji to na każdą jednostkę zbiorowości przypada taka część ogólnej sumy wartości (np. każdy pracownik w przedsiębiorstwie otrzymuje taką samą płacę)
gdy jest koncentracja zupełna - to łączymy fundusz cechy przypada na jednostkę zbiorowości (np. łączymy areał ziemi w województwie należy do jednego gosp. rolnego)
W rzeczywistości zjawiska te raczej nie występują. W praktyce statystycznej stosuje się zwykle dwie metody zjawisk:
graficzną
analityczną
Metoda graficzna polega na wykreśleniu tzw. Wieloboku koncentracji Lorenza.
1.Badanie statystyczne. Etapy badania i rodzaje badań statystycznych
Badanie statystyczne - ogół prac mających na celu poznanie prawidłowości występujących w procesach masowych. Przedmiotem badań są określone zbiorowości (populacje), które stanowią zbiór jednostek powiązanych ze sobą logicznie i jednocześnie nie identycznych. Etapy badania statystycznego:
-planowanie - sprecyzować cel badania ( wyjaśnić przyczyny zjawiska: zdefiniować zbiorowość statyst., dokonać wyboru cech statyst., które będą obserwowane)
-obserwacja statystyczna ( zbieranie danych liczbowych) - formy badania: obserwacje spisowe, bieżąca obserwacja, inne badania o charakterze i przeznaczeniu specjalnym. W wyniku otrzymujemy surowy materiał statyst.
-opracowanie zebranego materiału statyst - pogrupowanie i zliczanie materiału statyst., otrzymujemy szeregi statyst. (ciąg wielkości statystycznych rosnących lub malejących uporządkowanych według określonych cech
-opinia i wnioskowanie statyst.
Badanie całkowite - takie gdzie badaniem objęte są wszystkie jednostki badanej zbiorowości
Badanie częściowe - j.w. niektóre jednostki
Rodzaje badań częściowych:
-reprezentacyjne - część zbiorowości wybrana losowo
-monograficzne - ustalona część zbiorowości
-ankietowe - badanie sondażowe
2.Cechy statystyczne - klasyfikacja cech statystycznych, przykłady
Cecha statyst. - pewna własność (właściwość) jednostki statyst. wchodzącej w skład badanej zbiorowości np. wiek, płeć. Dzielimy na:
-ilościowe (mierzalne) - poszczególne ich warianty dają się wyrazić za pomocą liczb. Możemy podzielić na: ciągłe (wiek), tzn. może przyjmować dowolne wartości z pewnego przedziału liczbowego i skokowe (liczba dzieci w rodzinie), tzn. przyjmuje ona tylko niektóre wartości z pewnego przedziału.
cechy jakościowe (niemierzalne) - warianty ich wyrażamy za pomocą słów np. płeć, zawód.
3.Charakterystyka tablicy statystycznej. Symbole umowne stosowane w publikacjach
W postaci tablic najczęściej przedstawiamy rezultaty obserwacji statyst. . Tablice statyst. są liczbowym obrazem struktury badanej zbiorowości. Są formą statystycznego uporządkowania danych liczbowych w sposób umowny. Tablice statyst. są zbiorem szeregów statystycznych. Dzielimy je na: proste i kombinowane. Tablica, która zawiera jeden szereg nazywamy tablicą prostą. Tablice kombinowane składają się z kilku szeregów, przy czym obejmują one jedną zbiorowość statyst. scharakteryzowaną według dwóch lub więcej cech jednocześnie.
Zasadniczo każda tablica składa się z trzech części: tytuł i nr. Tablicy i informacje na temat budowy tablicy.
Budując tablice statyst. należy zwrócić uwagę aby każda jej pozycja była zapełniona odpowiednią liczbą. Jeśli z pewnych przyczyn nie możemy wypełnić jakiejś pozycji liczbą, to w tym miejscu stawiamy jeden z następujących znaków umownych:
-kreska (-) która oznacza, że dane zjawisko nie występuje
-kropka (.) która oznacza brak informacji lub brak wiarygodnych informacji o danym zjawisku
-zero (0) które oznacza, że dane zjawisko występuje, ale w ilościach rzędu mniejszego od rzędu liczb podanych w tablicy
-wykrzyknik (!) obok liczby używany jest dla podkreślenia, że została ona zamieszczona w tablicy jako poprawniejsza w porównaniu z poprzednio ogłoszoną
-krzyżyk (#) który oznacza, że rubryka nie może być wypełniona ze względu na układ tablicy.
Pod tablicą umieszcza się uwagi i odsyłacze, które zawierają dodatkowe wyjaśnienia dotyczące poszczególnych informacji lub całości tablicy.
4.Charakterystyka i zastosowanie klasycznych miar przeciętnych
![]()
Do miar średnich klasycznych zaliczamy :
-średnia arytmetyczna - stanowi ją suma wartości wszystkich jednostek zbiorowości statyst. podzielona przez liczebność tej zbiorowości
-średnia harmoniczna - stosujemy gdy wartości cechy podane są w formie odwrotności (gdy wartości jednej cechy są podane w przeliczeniu na stała jednostkę innej cechy), np. przeciętna prędkość pojazdów, towarów itd.
-średnia geometryczna - charakteryzuje cechę gdy wartości tej cechy przedstawione są w postaci względnej. Stosowana gdy występują duże różnice między obserwacjami, jest mniej wrażliwa na wartości nietypowe niż średnia arytmetyczna.
5.Charakterystyka i zastosowanie pozycyjnych miar przeciętnych
Do tych miar zaliczamy:
-dominanta (moda) - to wartość cechy, która w badanej zbiorowości występuje najliczniej i najczęściej. Można ją policzyć jeśli w szeregu wystąpi jedna największa wartość i rozpiętości przedziałów sąsiadujących są równe. Jest wielkością mianowaną.
-mediana - jest to ta wartość cechy, która występuje pośrodku uporządkowanego szeregu statyst. Jest wielkością mianowaną. Nie może być poddawana działaniom arytmetycznym.
-kwartyle - mediana jest nie kiedy nazwana drugim kwartylem. Występuje jeszcze pierwszy i trzeci kwartyl. Kwartyle obliczane z szeregu rozdzielczego są wartościami przybliżonymi. Wszystkie te miary są mianowane tzn. wyrażone w takich jednostkach jak badana cecha.
6.Charakterystyka i zastosowanie względnych i bezwzględnych miar zróżnicowania
Zadaniem miary zróżnicowania jest wskazanie w jakim stopniu poszczególne wartości cechy jednostki zbiorowości statyst. koncentrują się wokół średniej danej cechy. Pozwalają mierzyć zróżnicowanie wartości zmiennej w ramach badanej zbiorowości, informują jak duże są różnice między różnymi wartościami cechy a przeciętną.
Miary zróżnicowania dzielimy na:
-klasyczne (odchylenie standardowe, odchylenie przeciętne, wariancja)
-pozycyjne (rozstęp - obszar zmienności, odchylenie ćwiartkowe)
Miary zróżnicowania względne i bezwzględne:
-względne - stosujemy je zwłaszcza w dwóch przypadkach: 1. przy porównywaniu zróżnicowania tych samych cech o równym poziomie średniej arytmetycznej 2. przy porównywaniu różnoimiennych cech. Miary względne to współczynniki zmienności oparte na: odchyleniu przeciętnym, odchyleniu standardowym, odchyleniu ćwiartkowym. Duże wartości świadczą o silnym zróżnicowaniu wartości cechy.
-bezwzględne - wyrażają natężenie zróżnicowania w takich samych jednostkach jak badane cechy. Wartości mianowane. Są to : odchylenie standardowe, odchylenie przeciętne, odchylenie ćwiartkowe, wariancja i rozstęp.
7.Miary asymetrii ( skośności )
Za ich pomocą mierzymy czy odchylenia od wartości średnich w jedną stronę są mniej lub więcej liczne od odchyleń w drugą stronę. Wyróżniamy następujące miary służące do pomiaru kierunku i sił asymetrii:
-klasyczny współczynnik asymetrii ( którego znak informuje o kierunku asymetrii, a wartość bezwzględna o sile)
-współczynnik asymetrii oparty na kwartylach ( j.w.)
8.Charakterystyka, interpretacja i zastosowanie indywidualnych wskaźników dynamiki
Indywidualne wskaźniki dynamiki ( tzw. indeksy) służą do porównań wielkości zjawisk w dwóch okresach lub momentach czasu.
Indeksy indywidualne dzielimy na:
-jedno-punktowe - informują jak zmienia się wielkość zjawiska w porównaniu z wielkością zjawiska z okresu który został przyjęty jako podstawa porównań. Jest często wyrażany w procentach.
-łańcuchowe - charakteryzują zmiany wielkości zjawiska z okresu na okres do oceny zmiany wielkości zjawiska wykorzystywany jest miernik zwany przeciętnym okresowym tempem zmiany zjawiska - jest to średnia geometryczna z indeksów łańcuchowych
9.Charakterystyka, interpretacja i zastosowanie agregatowych indeksów dla wielkości absolutnych
Użyjemy agregatowych indeksów gdy składniki są niesumowalne. Stosowane są przy badaniach wielkości produkcji, dynamiki eksportu, importu.
Wyróżniamy:
-indeks wartości - informuje o tym jak zmienia się wartość produkcji przedsiębiorstwa w porównywanych okresach (podstawowym i badanym)
Indeksy pomocnicze:
-indeks ilości - otrzymujemy wówczas gdy formułę indeksu wartości ceny produkowanych towarów w porównywanych okresach nie zmieniały się.
-indeks ilości o formule Laspeyresa - otrzymujemy jeżeli przyjmiemy, że w porównywalnych okresach ceny jednostkowe towarów nie zmieniały się i były takie jak w okresie podstawowym.
-indeks ilości o formule Paaschego - jeżeli założymy, że w porównywalnych okresach ceny jednostkowe towarów nie zmieniały się i były takie jak w okresie badanym
-indeks cen - otrzymujemy gdy przyjmujemy założenie, że w porównywanych okresach ilości produkowanych towarów nie zmieniał się
-indeks cen o formule Laspeyresa - otrzymujemy jeżeli przyjmiemy, że ilości towarów w dwóch okresach były takie jak w okresie podstawowym
-indeks cen o formule Paaschego - otrzymujemy jeśli założymy, że w porównywalnych okresach ilości towarów nie zmieniały się i były takie jak w okresie badanym
10.Metody wyodrębniania wahań sezonowych
Wyróżniamy dwie metody:
-metoda mechaniczna - polega na wyrównywaniu szeregu czasowego poprzez obliczanie średnich ruchomych. Najczęściej używa się średnie ruchome 3-, 5-, 7 - okresowe. Dane dla kolejnych okresów zastępowane są średnimi ruchomymi z okresu badanego i kilku okresów przyległych. Polega na wyznaczaniu linii wokół której układają się punkty na wykresie przedstawiające dane zjawiska (linia trendu ). Linia trendu służy do przewidywania zjawiska w przyszłości. Każda prognoza obarczona jest błędem wyrażonym przez odchylenie standardowe resztowe.
-metoda analityczna
11.Analityczna metoda wyodrębniania wahań sezonowych
W pierwszym etapie wyznaczamy równanie linii trendu, następnie obliczamy wskaźnik
sezonowości brutto
![]()
![]()
gdzie: ∑yi(t) i ∑yˆi(t) ozn. odpow. sumy wartosci empirycznych i teoretycznych dla okresow jednoimiennych.
![]()
Jeśli
(d-liczba okresow), to obliczamy skorygowane wsk. sezonowosci: O=O`i : R
![]()
,gdzie:
12.Metody pomiaru zależności korelacyjnej dwóch cech w przypadku korelacji krzywoliniowej
Jeżeli wartością jednej z cech odpowiadają zmiany średnich z kilku wartości innej cechy to powiemy, że między tymi cechami występuje zależność korelacyjna. Jeżeli punkty na płaszczyźnie przedstawiające wartości cech skupiają się wokół pewnej linii krzywej to powiemy, że między badanymi cechami występuje zależność korelacyjna krzywoliniowa. Miary siły związku korelacyjnego dwóch cech w przypadku zależności krzywoliniowej:
-współczynnik korelacji rang - rangą wartości cechy nazywamy numer miejsca jakie zajmuje ta wartość cechy po uporządkowaniu w sposób niemalejący wszystkich wartości cech. Wykorzystywany jest do badania siły i kierunku zależności korelacyjnej między dwoma cechami mierzalnymi zarówno prosto jak i krzywoliniowej. Może być też stosowany w przypadku cech niemierzalnych pod warunkiem, że wartości tych cech dadzą się uporządkować . Jest to miara unormowana, która spełnia zależność -1=< R =< 1. O sile zależności informuje /R/ : bliskie jedności jego wartości oznaczają b. silną korelację natomiast wartości bliskie zeru b. słabą zależność bądź jej brak. O kierunku zależności korelacyjnej informuje znak współ. R.
-Stosunek korelacji- stosuje się gdy jedna z cech jest niemierzalną (choć może być mierzalna). Obliczany jest z danych pogrupowanych w tabeli korelacyjnej. Może być stosowany do zależności krzywo i prosto liniowych. Miara jest wielkością unormowaną .Korelacja pomiędzy cechami jest tym silniejsza im bliższy jedności jest stosunek korelacji. Między cechami występuje zależność funkcyjna. Miara ta jest niesymetryczna
-Współczynnik kontygnencji C-Pearsona- Wykorzystywany jest przede wszystkim do badania siły zależności korelacyjnej między dwiema cechami mierzalnymi. Miernik ten jest wielkością unormowaną i zawsze spełnia nierówność 0=<C=<1. Bliskie zeru wartości oznaczają ,że między badanymi cechami występuje bardzo słaba zależność bądź też zależności tej nie ma. Natomiast bliskie 1 oznaczają bardzo silną zależność. Miernika tego można używać zarówno do badania zależności prosto i krzywoliniowych.
13.Funkcja regresji. Metoda szacowania parametrów równania linii regresji. Zast.
Funkcja regresji może służyć do przewidywania wartości jednej cechy przy określonym poziomie drugiej cechy. Związek między dwoma cechami można opisać za pomocą funkcji postaci y^=a+bx .Parametry a i b wyznaczamy z układu równań normalnych, którego rozwiązaniem są poszukiwane parametry linii regresji. Układ równań nazywany jest układem równań normalnych, a zastosowana metoda, która prowadzi do tego układu nosi nazwę metody najmniejszych kwadratów.
14. Miary ścisłości związku korelacyjnego w przypadku korelacji prostoliniowej.Stopień zależności pomiędzy dwoma badanymi cechami mierzalnymi X Y które pozostają w związku liniowym określane za pomocą:
-Współczynnika korelacji r..
-Współczynnik korelacji rang Spearmana
-Stosunek korelacji e.. określony jest jako udział zmienności objaśnionej w zmienności całkowitej gdy e..=1 gdy między cechami XY istnieje zależność funkcyjna, gdy e..=0 cech są nieskorelowane.
15. Regresja krzywoliniowa, kryteria wyboru optymalnej postaci funkcji regresji
Po ustaleniu, że między rozważanymi cechami istnieje korelacja, przechodzimy do znalezienia funkcji regresji, która może służyć do przewidywania wartości jednej cechy przy określonym poziomie drugiej cechy. Jeżeli punkty na płaszczyźnie oznaczające wartości obu cech, skupiają się wzdłuż pewnej linii krzywej, to powiemy, że między badanymi cechami występuje zależność krzywoliniowa.
Krzywoliniowa funkcja regresji może mieć postać:
1. ![]()
(dla cechy X: ![]()
)
2. ![]()
po transformacji mamy postać liniową:![]()
Aby wybrać najlepszą z możliwych funkcji regresji stosujemy metodę najmniejszych kwadratów:
1.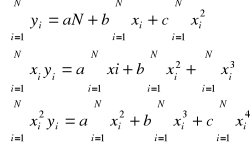
Otrzymaliśmy układ równań o niewiadomych a, b, c, których rozwiązaniami są poszukiwane parametry równań funkcji regresji. Ten układ równań nazywamy układem równań normalnych. Najlepszą z możliwych funkcji regresji charakteryzuje wysoki współczynnik determinacji:
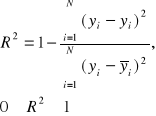
Współczynnik ten informuje w ilu % zmienność cechy Y wyjaśniana jest zmiennością cechy X, a tym samym o stopniu dopasowania linii regresji do danych empirycznych. Im wartość współczynnika determinacji jest bliższa 1, tym lepszy stopień dopasowania.
16. Estymatory i ich własności
Załóżmy, że dystrybuanta F(x, θ) charakteryzuje rozkład populacji generalnej, gdzie θ jest nieznanym parametrem. Niech x1, ..., xn będzie n-elementową próbą wylosowaną z tej populacji. Statystykę Tn która jest funkcją tej próby służącą do oszacowania θ nazywać będziemy estymatorem. Wartość tej funkcji (tn) nazywać będziemy oceną estymatora (konkretna liczba odpowiadająca danej realizacji próby).
Cechy dobrego estymatora:
-zgodność estymatora Tn parametru θ
![]()
W miarę wzrostu liczebności próby prawdopodobieństwo przekroczenia dowolnie małej różnicy spada do 0
-nieobciążalność parametru
estymator Tn jest nieobciążalnym estymatorem parametru θ jeżeli wartość nieoczekiwana E(Tn)=θ. Jeżeli przy pomocy nieobciążalnego estymatora szacujemy parametr θ, to chociaż w poszczególnych przypadkach uzyskiwane cechy mogą się różnić od wartości parametru θ, to w dużej serii średnia takich ocen będzie bliska 0
-efektywność estymatora
estymator Tn jest najefektywniejszy jeżeli wśród estymatorów nieobciążalnych ma on najmniejszą wariancję
-wystarczalność
Estymator Tn jest wystarczalny jeśli zawiera wszystkie tkwiące w próbie informacje o θ
17. Metoda estymacji przedziałowej średniej w zbiorowości generalnej
Załóżmy, że badamy pewną zmienną X, która w zbiorowości generalnej ma rozkład X~N(m,σ) przy czym znamy wartość σ. Ze zbiorowości tej losujemy
n-elementową próbę. Chcemy oszacować parametr m (θ=m). Estymatorem tego parametru, posiadającym wszystkie cechy dobrego estymatora jest średnia arytmetyczna z próby (Tn=![]()
) Przedział ufności dla szacowanego parametru ma postać: 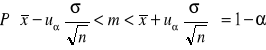
uα - wielkość odczytywana z tablic dystrybuanty rozkładu normalnego w oparciu o zależność:![]()
2) θ=m, Tn=![]()
, X~N(m,σ), nie znamy σ
Przedział ufności ma postać:
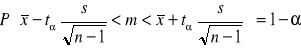
tα - wielkość odczytywana z tablicy rozkładu t-Studenta w oparciu o zależność:, dla n-1 st.
swobody![]()
3) ) θ=m, Tn=![]()
, X rozkład nieznany, nie znamy σ, n>30
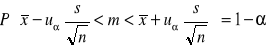
18. Niezbędna liczebność próby
Chcemy oszacować nieznaną średnią wartość m w zbiorowości na podstawie
n-elementowej próby, aby przy ustalonym współczynniku ufności 1-α, max. błąd szacunkowy nie przekroczył z góry określonej liczby d
1) θ=m, Tn=![]()
, X~N(m,σ), znamy σ
Niezbędna liczebność próby wynosi:
![]()
2) θ=m, Tn=![]()
, X~N(m,σ), nie znamy σ
Niezbędna liczebność próby wynosi:
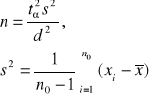
3) θ=p, znany jest rząd wielkości p
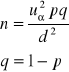
4) θ=p, nie znany jest rząd wielkości parametru p
![]()
19. Metody szacowania miar zróżnicowania w przypadku częściowego badania statystycznego
Do klasycznych miar zróżnicowania zaliczamy m.in. wariancję i odchylenie standardowe
-przedział ufności dla wariancji
X~N(m,σ), θ=σ², Tn=s², n nie musi być duże
Przedział ufności dla wariancji ma postać:
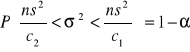
parametry c1 i c2 odczytujemy z tablic wartości krytycznych rozkładu χ² dla n-1 stopni swobody i w oparciu o zależności:
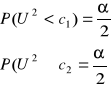
-przedział ufności dla odchylenia standardowego
X ma dowolny rozkład, n>30, θ=σ, Tn=s
Przedział ufności dla odchylenia standardowego ma postać:
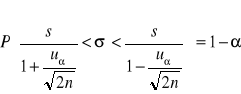
uα odczytujemy z tablic dla współczynnika ufności 1-α, tak aby spełniona była relacja: P{-Uα<U<Uα}=1-α
20. Weryfikacja hipotezy o równości dwóch średnich przy założeniu normalności rozkładu badanej zmiennej w zbiorowościach generalnych
1) N(m1,σ1) i N(m2,σ2)
znamy σ1, σ2
na podstawie wyników z prób (o liczebnościach n1, n2) wyznaczamy wartość statystyki:
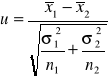
statystyka ta przy założeniu prawdziwości H0 ma rozkład normalny N(0,1)
dla przyjętego poziomu istotności α wartości krytyczne uα odczytujemy tak, by spełnione były równości:
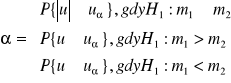
gdy:
![]()
to H0 odrzucamy na rzecz H1: m1≠m2
![]()
to H0 odrzucamy na rzecz H1: m1<m2
![]()
to H0 odrzucamy na rzecz H1: m1>m2
2) jeżeli nie mamy podstaw do przyjęcia założenia o normalności rozkładów postępujemy analogicznie, ale zamiast nieznanych σ1², σ2² wstawiamy s1², s2²
3) Jeżeli N(m1,σ1) i N(m2,σ2) i nie znamy σ1, σ2 ale wiemy że σ1=σ2,
to korzystamy z testu Studenta:
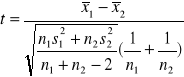
statystyka ta ma przy założeniu prawdziwości H0 rozkład Studenta o n1+n2-2 stopniach swobody oraz dla założonego α taką wartość tα, że:
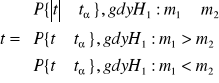
Jeśli spełniona jest co najmniej jedna nierówność odrzucamy H0
Jeżeli wiemy że: N(m1, σ1) i N(m2, σ2) ale nie znamy parametrów należy najpierw zweryfikować:
H0: σ1²=σ2²
H1: σ1²>σ2²
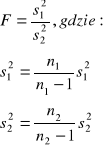
Statystyka F ma przy założeniu prawdziwości H0 rozkład F Snedecora o r1= n1-1 i r2=n2-1 stopniach swobody
Fα odczytujemy z tablic, gdy F>Fα odrzucamy H0
21. Estymacja przedziałowa wskaźnika struktury
θ=p - wskaźnik struktury zbiorowości
Tn= k/n - wskaźnik struktury z próby
n>100
Przedział ufności ma postać:
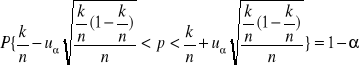
k - liczba jednostek wyróżnionych z n-elementowej próby
uα odczytujemy z tablicy rozkładu normalnego
Weryfikacja hipotezy o równości dwóch wskaźników struktury
n1,n2>100
H0: p1=p2
H1: p1≠p2
Obliczamy wartość statystyki:
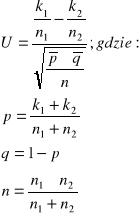
Statystyka U ma przy założeniu prawdziwości H0 rozkład N(0,1)
jeżeli ![]()
to H0 odrzucamy na rzecz H1: m1≠m2
22. Testy normalności
Testy normalności są testami nieparametrycznymi, służą do weryfikacji hipotezy o rozkładzie normalnym cechy X w zbiorowości generalnej.
1) Test zgodności χ²
dana jest duża próba
H0: F(x)∈ω
H1: ~H0
budujemy szereg rozdzielczy o przedziałach klasowych o liczebnościach ni, przy czym w każdej klasie musi być co najmniej 8 elementów
![]()
następnie trzeba obliczyć prawdopodobieństwo że zmienna losowa o dystrybuancie F(x) przyjmie wartości należące do i-tej klasy
![]()
Wartość statystyki obliczamy ze wzoru:
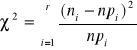
r - liczba przedziałów
ni - liczebność i-tego przedziału
npi - liczebność teoretyczna
przy danym poziomie istotności α odczytuje się z tablic rozkładu χ² dla r-k-1 stopni swobody (k - liczba szacowanych parametrów; najczęściej 2 - średnia i wariancja) wartość krytyczną χ²α
Jeżeli zachodzi nierówność χ² < χ²α to odrzucamy H0
2) Test normalności Shapiro - Wilka
dana jest mała próba
H0: F(x)=F0(x); gdzie F0(x) jest dystrybuantą rozkładu normalnego
H1: ~H0
obliczamy wartość statystyki:
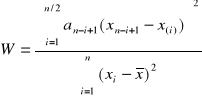
n/2 - część całkowita n/2
x(i) - uporządkowany rosnąco ciąg wartości zmiennej
an-i+1 - odczytujemy z tablic współczynników dla testu normalności Shapiro - Wilka
odczytujemy Wα z tablicy wartości krytycznych dla testu normalności Shapiro - Wilka
jeżeli W≥Wα nie ma podstaw do odrzucenia H0
23. Test niezależności χ²
Zbiorowość generalna badana jest ze względu na dwie cechy niekoniecznie mierzalne. Ze zbiorowości losujemy próbę n - elementową. Wyniki próby grupujemy tworząc tablicę niezależności o r wierszach i s kolumnach. Grupowanie przeprowadzamy w ten sposób, aby w każdym polu tablicy liczba elementów była równa co najmniej 8. Sprawdzamy czy badane cechy są niezależne:
H0: P(x=xi; y=yj) = p(x=xi)P(y=yj)
H1: ~H0
Sprawdzianem tej hipotezy jest:
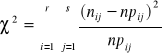
Wartość sprawdzianu porównujemy następnie z wartością krytyczną χ²α którą przy danym poziomie istotności α i dla (r-1)(s-1) stopni swobody odczytujemy z tablic rozkładu χ² w oparciu o zależność: P(χ²≥χα²)=α
Jeżeli: χ²≥χα² to odrzucamy H0
Pomiar siły korelacji dwóch cech niemierzalnych
Współczynnik kontyngencji C - Pearsona
Miernik ten jest wielkością unormowaną; spełna w-k: C∈<0,1>
Bliskie 0 wartości świadczą o bardzo słabej zależności między cechami. Wartości bliskie 1 oznaczają bardzo silną zależność.
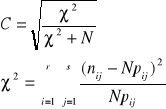
24. Charakterystyka i zastosowanie testów serii
Testy serii to testy nieparametryczne stosowane dla sprawdzenia hipotezy tylko wówczas gdy nie można wykorzystać testów parametrycznych ze względu na wymagane założenia.
1) Test serii losowości próby
Z badanej zbiorowości pobieramy próbę n - elementową.
H0: wybrana próba jest losowa
H1: ~H0
Test istotności:
Z uporządkowanego wg kolejności pobierania elementów ciągu wyników próby obliczamy medianę.
Każdemu wynikowi przypisujemy symbol: „a” jeśli xi<Me lub „b” jeśli xi>Me.
Wynik xi=Me odrzucamy.
Otrzymujemy ciąg symboli „a” i „b”. Obliczamy liczbę serii k.
Z tablic rozkładu liczby serii przy danym poziomie istotności α odczytujemy takie dwie wartości krytyczne k1 i k2 aby spełnione były relacje:
P(k≤k1)=α/2
P(k>k2)=1-α/2
Jeżeli: k1<k<k2 nie mamy podstaw do odrzucenia H0
2) Test serii sprawdzający hipotezę, że dwie próby pochodzą z jednej zbiorowości
Dane są dwie zbiorowości, z których wylosowano próby o liczebnościach n1 i n2. Na podstawie wyników tych prób należy sprawdzić hipotezę, że próby te pochodzą z jednej zbiorowości (rozkłady badanych zbiorowości nie różnią się).
Test istotności:
Wyniki dwóch prób ustawiamy rosnąco w jeden ciąg. Elementy próby z I zbiorowości oznaczamy „a”, a elementy z II próby „b”. Odczytujemy z tablic rozkładu liczby serii dla przyjętego poziomu istotności α oraz liczb n1, n2 wartość krytyczną kα. Jeżeli k≤kα to odrzucamy H0.
Statystyka - ściąga
36
![]()
![]()
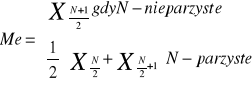
![]()
![]()
![]()
![]()
![]()
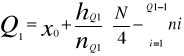
![]()
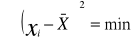
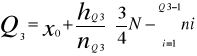
![]()
![]()
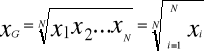
![]()
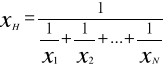
![]()
![]()
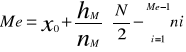
![]()
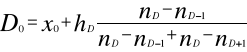
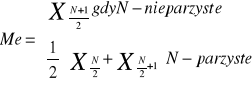
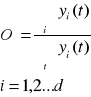
![]()
![]()
![]()
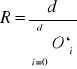
Wyszukiwarka