Praca klasowa nr 8 - zakres rozszerzony

Wielomiany i funkcje wymierne

Zadanie 1

Dany jest wielomian
Stopień wielomianu
jest równy:

A. 2 B. 3 C. 5 D. 6

Zadanie 2

Wykres funkcji
nie ma punktów wspólnych z prostą:

A.
B.
C.
D.

Zadanie 3

Rozwiązaniem równania
jest:

A.
B.
C.
D.

Zadanie 4

Dziedziną funkcji
jest zbiór
, zatem:

A.
B.
C.
D.

Zadanie 5

Dla
wyrażenie
można zapisać w postaci:

A.
B.
C.
D.

Zadanie 6

Rozwiąż.

1. 
   

2. 
   

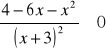
Zadanie 7

Naszkicuj wykres funkcji

Zadanie 8

Po remoncie nawierzchni średnia prędkość samochodu jadącego z miejscowości A do B wzrosła o
, a czas przejazdu skrócił się o 40 minut. Oblicz, z jaką średnią prędkością jeżdżą teraz tą trasą samochody, jeśli miejscowości są oddalone od siebie o

Zadanie 9

Wyznacz resztę z dzielenia wielomianu
przez wielomian
wiedząc,

że

Zadanie 10

Wykaż, że jeżeli
to największą wartością wyrażenia
jest

Model odpowiedzi i schemat oceniania pracy klasowej nr 8 - zakres rozszerzony

Maksymalna liczba punktów do zdobycia: 19 + 2

Numer zadania	Etapy rozwiązania zadania	Liczba punktów
1.	D	1
2.	B	1
3.	A	1
4.	B	1
5.	C	1
6.	a) Przekształcenie równania do postaci Uwaga: Jeśli uczeń popełni jeden błąd rachunkowy, to przyznajemy 1 punkt.	2
		a) Rozwiązanie równania i podanie odpowiedzi:	1
		b) Zauważenie, że dana nierówność jest równoważna nierówności dla	1
		b) Rozwiązanie nierówności i podanie odpowiedzi:	1
	7.	Naszkicowanie wykresu funkcji	1
		Naszkicowanie wykresu funkcji	1
	8.	Zapisanie zależności między drogą, prędkością i czasem: , gdzie oznacza średnią prędkość, z jaką jeździły samochody przed remontem	1
		Przekształcenie równania do postaci	1
		Rozwiązanie równania: i podanie odpowiedzi: samochody jeżdżą obecnie z prędkością	1
	9.	Zauważenie, że reszta z dzielenia wielomianu przez wielomian ma postać i zapisanie wielomianu w postaci	1
		Zauważenie, że pierwiastkami wielomianu są liczby i 3	1
		Zastosowanie twierdzenia o reszcie i zapisanie warunków:	1
		Rozwiązanie układu równań i podanie odpowiedzi:	1
	10.	Zastosowanie wzoru skróconego mnożenia oraz podanej zależności i przekształcenie danego wyrażenia do postaci	1
		Uzasadnienie, że największą wartością danego wyrażenia jest	1

Przykładowa ocena pracy klasowej

Liczba x uzyskanych punktów	6	6 9	9 14	14 18	18 19	19
Ocena	1	2	3	4	5	6
Maksymalna liczba punktów: 19 + 2

Autorzy:

Agnieszka Kamińska

Dorota Ponczek