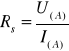Politechnika Lubelska w Lublinie		Laboratorium podstaw elektrotechniki Ćwiczenie Nr 4
Nazwisko: Podleśny Wojewódzka Wojtanowski Wrońska	Imię: Marek Katarzyna Łukasz Anna	Semestr II	Grupa E.D.2.3	Rok akademicki 2000/01
Temat ćwiczenia : Obwody nieliniowe prądu stałego			Data wykonania : 15.III.2001	Ocena :

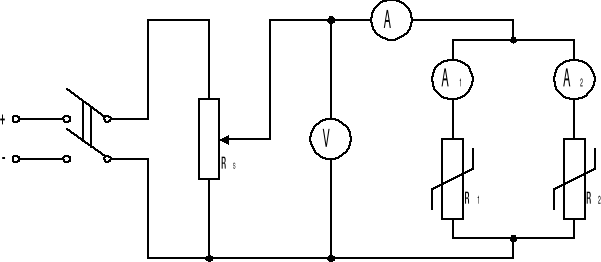
1. Wyznaczanie charakterystyki elementów nieliniowych.

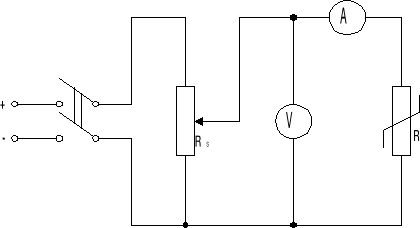
Rysunek 1 - Układ pomiarowy charakterystyki pojedynczego elementu nieliniowego,

Wyniki pomiarów :

Tabela 1

Lp.	Element 1		Element 2		Połączenie szeregowe 1+2		Połączenie równoległe 1+2
		U	I	U	I	U	I	U	I
		[V]	[A]	[V]	[A]	[V]	[A]	[V]	[A]
1 2 3 4 5 6	2,5 7 11 15 20 24	0,077 0,12 0,155 0,185 0,21 0,23	3 7 11 15 20 24	0,06 0,085 0,11 0,13 0,145 0,16	3 7 11 16 20 24	0,055 0,075 0,09 0,11 0,12 0,13	2,5 6,5 10,5 15 19 24	0,13 0,2 0,265 0,31 0,35 0,39

Gdzie : element 1 - żarówka 60 W, element 2 - żarówka 40 W.

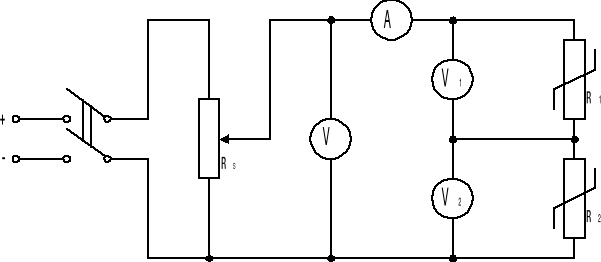
2. Pomiar charakterystyki połączenia szeregowego dwóch elementów nieliniowych.

Rysunek 2 - Układ pomiarowy dla połączenia szeregowego,

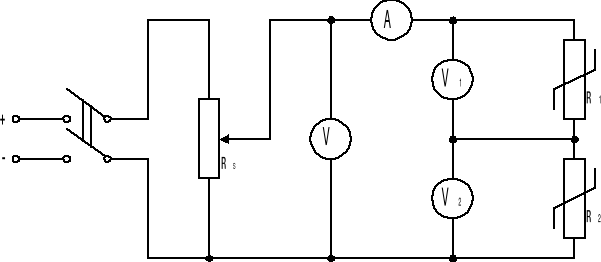
Wyniki pomiarów :

Tabela 2 Tabela 3

Lp.	U	I		Metoda	I	U1			U2
		[V]			[A]			[A]	[V]			[V]
1	7	0,075				b	0,075		2	5
2	16	0,11
3	24	0,13

Gdzie b, oznacza wynik otrzymany w następujący sposób :

b) na podstawie pomiaru

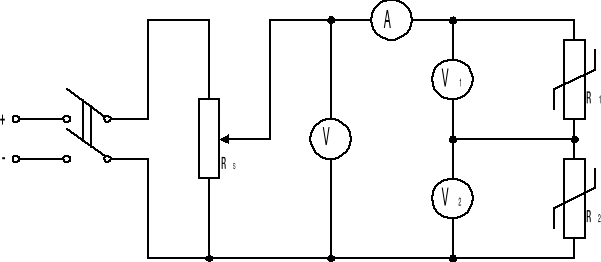
3. Pomiar charakterystyki połączenia równoległego dwóch elementów nieliniowych,

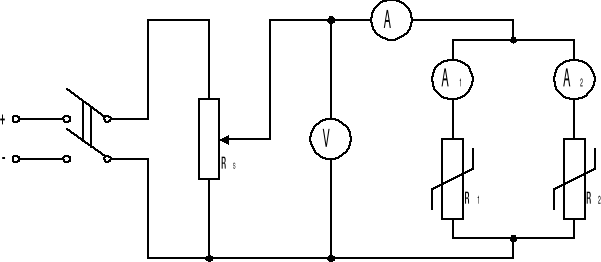
Rysunek 3 - Układ pomiarowy dla połączenia równoległego,

Wyniki pomiarów :

Tabela 4 Tabela 5

Lp.	I	U		Metoda	U			I1	I2
		[A]			[V]			[V]			[A]	[A]
1	0,95	1			b		1	0,41		0,575
2	1,4	3,5
3	1,8	6

Gdzie b, oznacza wynik otrzymany w następujący sposób :

b) na podstawie pomiaru

4, Rezystancja statyczna i dynamiczna.

Element 1:

Przy napięciu 2,5 V przez element 1 płynie prąd 0,077 A, a więc rezystancja statyczna elementu 1 wynosi 32,46 Ω

Przy napięciu 24 V przez element 1 płynie prąd 0,23 A, a więc rezystancja statyczna elementu 1 wynosi 104,34 Ω

Element 2:

Przy napięciu 3 V przez element 2 płynie prąd 0,06 A, a więc rezystancja statyczna elementu 2 wynosi 54,54 Ω

Przy napięciu 24 V przez element 2 płynie prąd 0,16 A, a więc rezystancja statyczna elementu 2 wynosi 150 Ω

Rezystancję statyczną elementu nieliniowego oblicza się w obranym punkcie według wzoru:

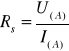
Rezystancja dynamiczna:

Element 1:

Przy napięciu 2,5 V przez element 1 płynie prąd 0,077 A, a więc rezystancja statyczna elementu 1 wynosi 1,23 Ω

Przy napięciu 24V przez element 1 płynie prąd 0,23 A, a więc rezystancja statyczna elementu 1 wynosi 0,38 Ω

Element 2:

Przy napięciu 3 V przez element 2 płynie prąd 0,06 A, a więc rezystancja statyczna elementu 2 wynosi 0,8 Ω

Przy napięciu 24 V przez element 2 płynie prąd 0,16 A, a więc rezystancja statyczna elementu 2 wynosi 0,26 Ω

Rezystancję statyczną elementu nieliniowego oblicza się w obranym punkcie według wzoru:

Rezystancję dynamiczną obwodu nieliniowego oblicza się w obranym punkcie według wzoru:

m_u - skala napięcia

m_i - skala prądu

• 
  kąt stycznej do charakterystyki prądowo - napięciowej.

R=m_u/m_i*tg

U=2,5V , I=0,23A ; m_u = 2V/1cm ; m_i - 0,05A/1cm; tg  U/I=10,8 Ω

5. Aproksymacja charakterystyk doświadczalnych.

Lp.	U		log U	I		log I
		[V]		-	[A]		-
1	2,5		0,39	0,13		-0,88
2	24	1,38		0,39	-0,40

Przyrządy pomiarowe:

• amperomierz -LM -3 3308045,76

- amperomierz-LM-1 2306191

• amperomierz-TLME-2 2302515

• woltomierz-LM-3 3806055,78

• woltomierz-TME-2 2309072

• woltomierz-LM-3 3404105,76

Wnioski:

Obwody elektryczne zawierające elementy, których parametry zależą od prądu płynącego przez element, bądź od napięcia występującego na zaciskach elementu nazywamy obwodem nieliniowym

W rzeczywistości wszystkie obwody elektryczne są nieliniowe. W określonych jednak warunkach i dla pewnych zakresów zmienności prądu i napięcia można wiele elementów zaliczyć do klasy liniowych, ale zawsze ma to charakter przybliżony. Przykładowo przy bardzo wielkich prądach następuje silne nagrzanie przewodnika i z tym jest związana zmiana rezystancji.

Przy bardzo wysokich napięciach następują z kolei zmiany w strukturze dielektryków. Kondensator może być liniowy dla określonego zakresu zmienności natężenia pola elektrycznego, a poza tym zakresem staje się nieliniowy.

Wiele jednak elementów musimy zaliczyć do grupy elementów nieliniowych w normalnym stanie pracy. Charakterystyki elementów nieliniowych rezystancyjnych uzyskuje się przeważnie w wyniku pomiarów, a przebieg charakterystyk przedstawia się w postaci wykresów zależności napięcia prądu lub odwrotnie.

Cechą zasadniczą obwodów nieliniowych jest to, że nie spełniają one zasady superpozycji. Rzutuje to na metody analizy tych obwodów. Dla obwodów nieliniowych słuszne są prawa Kirchoffa dla wartości chwilowych. Stosowanie tych praw jest konieczne zarówno w posługiwaniu się w obliczeniach metodami analitycznymi jak i graficznymi.

Przy obliczaniu obwodów nieliniowych, zwłaszcza prądu stałego, stosuje się metody graficzne oraz numeryczne.

1



---