![]()
![]()
(8.75)
Ostatnie równanie dowodzi, że:
![]()
![]()
(8.75)
Podstawiamy wyrażenie na ![]()
z (8.75) do (8.73) i otrzymujemy równanie dla funkcji
![]()
Zatem
![]()
,
gdzie A i B są dowolnymi stałymi. Jeżeli dla ustalonego y, to i
![]()
Jeżeli dla ustalonego t, to oraz:
![]()
,
![]()
Stąd wynika, że dla ustalonej wartości y prędkość dąży do V, gdy , tzn. w miarę upływu czasu ścianka nadaje danej cząstce cieczy prędkość ![]()
Przykład 8.7. Należy wykazać występowanie paradoksu Stokesa, uniemożliwiającego konstruowanie przepływów pełzających w płaskich obszarach nieograniczonych, rozważając zagadnienie opływu cylindra o promieniu R jednorodnym strumieniem stacjonarnym cieczy lepkiej (rys. 8.12).
Do rozwiązania zagadnienia użyjemy równania Stokesa ruchu cieczy lepkiej w układzie współrzędnych cylindrycznych. Wprowadzając funkcję prądu, spełniającą równanie ciągłości, określoną związkami:
![]()
,
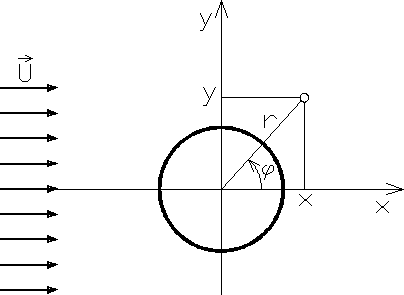
Rys. 8.12
możemy zapisać równanie Stokesa w postaci równania biharmonicznego
![]()
(8.76)
Do rozwiązania równania (8.76) zastosujemy metodę rozdzielenia zmiennych przyjmując
![]()
Po podstawieniu będziemy mieli:
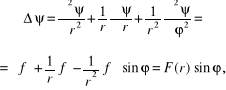
![]()
Rozwiązanie ogólne tego równania różniczkowego
![]()
ma postać
![]()
.
Powrót do funkcji f daje równanie różniczkowe
![]()
i następnie otrzymujemy:
![]()
![]()
Wracając do funkcji prądu i wyrażeń dla składowych wektora prędkości uzyskujemy:
![]()
![]()
![]()
gdzie wartości stałych całkowania A, B, C są wyznaczane z warunków brzegowych.
W nieskończenie wielkiej odległości od cylindra funkcja prądu powinna być równa funkcji prądu dla opływu cylindra cieczą doskonałą, co wymaga spełnienia warunku
![]()
Z tego warunku wynika, że powinny znikać stałe A i B oraz należy przyjąć:
C = U. Jedyna pozostała stała D nie może jednak spełniać równocześnie dwóch warunków znikania na okręgu składowych i wektora prędkości ![]()
Przykład 8.8. Kula o promieniu a, umieszczona w nieograniczonej przestrzeni wypełnionej cieczą lepką , obraca się z prędkością kątową wokół osi z. Zbadać ruch cieczy wywołany obrotem kuli, jeżeli obrót kuli jest powolny (ω małe).
Jako prędkość charakterystyczną ruchu możemy przyjąć prędkość punktów równika kuli równą ![]()
wtedy liczba Reynoldsa
![]()
.
Ponieważ prędkość kątowa jest mała, więc liczba Reynoldsa też będzie mała. Na mocy tego założenia w równaniach ruchu, zapisanych w układzie współrzędnych sferycznych ![]()
możemy odrzucić ich lewe strony. Tak otrzymane równania ruchu będą spełnione, jeżeli przyjmiemy, że ![]()
![]()
prędkość będzie zależeć tylko od r i θ
i powinna spełniać równanie
![]()
(8.77)
Na powierzchni kuli cząstki cieczy powinny poruszać się z tą samą prędkością liniową ![]()
jaką mają punkty kuli, stąd mamy warunek graniczny
![]()
(8.78)
Na mocy warunku (8.78) będziemy poszukiwać rozwiązania równania (8.77) w po-staci
![]()
(8.79)
Po podstawieniu (8.79) do (8.77) uzyskujemy równanie różniczkowe Eulera
![]()
którego rozwiązaniem ogólnym jest funkcja
![]()
Stałe całkowania ![]()
, wyznaczamy z warunków brzegowych. Otóż, dla powinno być V = 0, stąd ![]()
Z warunku (8.83) znajdziemy, że ![]()
więc
![]()
.
Obliczymy jeszcze wielkość momentu konieczną do podtrzymania ruchu kuli. Naprężenia styczne (sił tarcia) na powierzchni kuli:
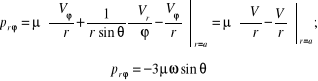
i moment sił tarcia
![]()
![]()
Moment potrzebny do utrzymania ruchu jest więc równy: ![]()
Przykład 8.9. Dwie okrągłe płaskie równoległe płytki o promieniu R każda, znajdując się w niewielkiej odległości jedna nad drugą, zbliżają się jednostajnie do siebie. Określić ruch warstwy cieczy zawartej między płytkami oraz wyznaczyć siły oporu działające na każdą z płytek.
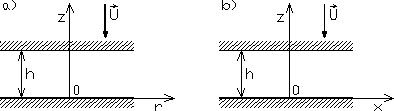
Rys. 8.13
Wprowadzając założenia upraszczające, analogiczne do założeń przyjętych w rozdziale 8.6, układ równań (8.38), zapisany (rys. 8.13a) we współrzędnych walcowych dla składowych wektora prędkości:
![]()
,
zredukuje się do postaci:
![]()
![]()
Ze względności ruchu wynikają warunki brzegowe:
u = w = 0 dla z = 0 ,
u = 0, w = − U dla z = h ,
dla r = R ;
tutaj U jest prędkością górnej płytki (dolną uważamy za nieruchomą), h jest grubością warstwy
Całkując równanie ruchu względem z (tj. w poprzek warstwy) i uwzględniając warunki brzegowe znajdziemy:
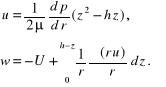
(8.80)
Po podstawieniu pierwszego z tych równań do drugiego
![]()
(8.81)
Zakładając z = 0 w górnej granicy całkowania, po wykonaniu działań otrzymamy
![]()
,
a po rozwiązaniu i uwzględnieniu warunku brzegowego znajdziemy
![]()
(8.82)
Siła oporu działająca na każdą z płytek równa się
![]()
.
Uwzględniając zależność (8.82) we wzorach (8.80) i (8.81) wyznaczamy składowe ektora prędkości:
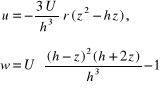
.
*
Rozważane zagadnienie można również rozwiązać posługując się układem równań (8.38), zapisanych w układzie współrzędnych prostokątnych (rys. 8.13b):
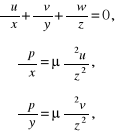
dla składowych wektora prędkości:
![]()
Warunki brzegowe mają postać:
![]()
dla
![]()
dla
dla
Całkując równania ruchu względem z i uwzględniając sformułowane warunki brzegowe znajdziemy:
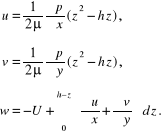
Po podstawieniu dwóch pierwszych równań do trzeciego mamy
![]()
Założenie z = 0 w górnej granicy całkowania prowadzi do równania Poissona dla ciśnienia
![]()
.
Poszukując rozwiązania tego równania w postaci funkcji
![]()
po uwzględnieniu warunku brzegowego: dla ![]()
otrzymamy
![]()
,
a następnie wyrażenia dla składowych prędkości:
![]()
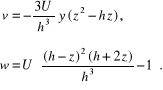
Przykład 8.10. Dwie płaszczyzny, tworzące ze sobą bardzo mały kąt ![]()
przesuwają się względem siebie ze stałą prędkością U (rys. 8.14). Obszar między tymi płaszczyznami wypełnia ciecz lepka. Należy wyznaczyć ciśnienie i siły działające na górną płaszczyznę.
Dla stacjonarnego przepływu jednowymiarowego równanie Reynoldsa (8.61) upraszcza się do postaci
![]()
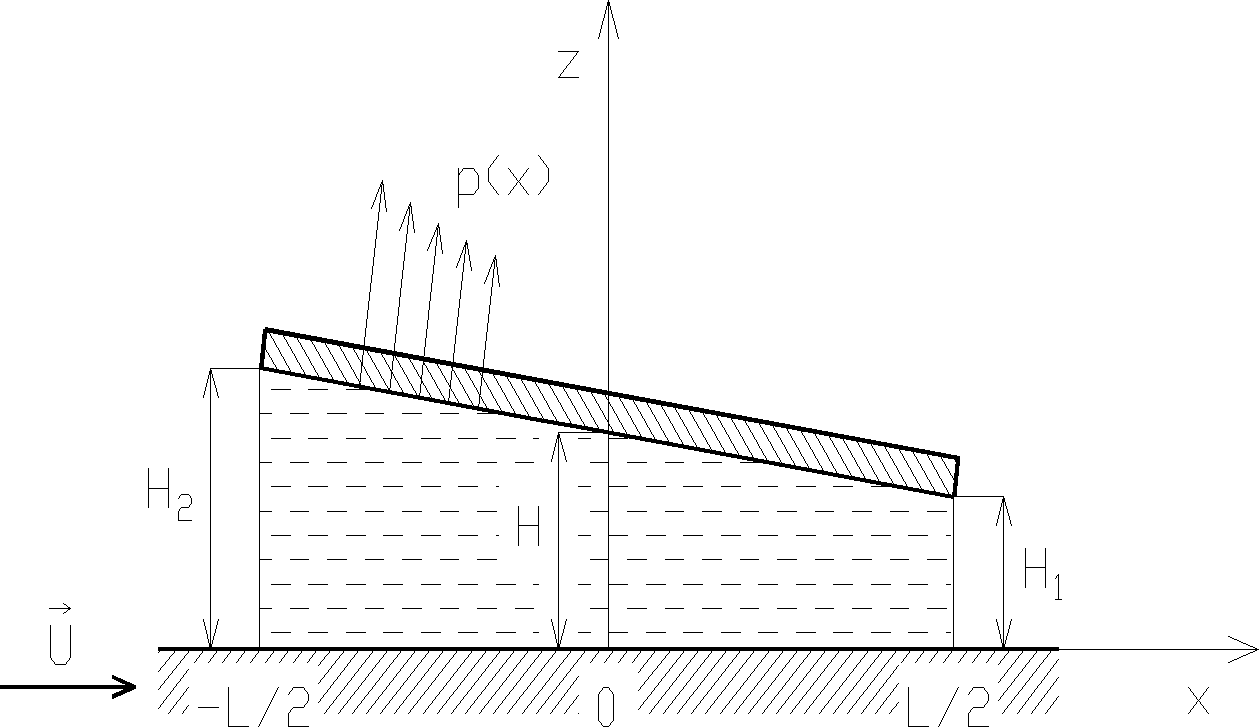
Rys. 8.14
skąd jest
![]()
i następnie
![]()
Po kolejnym całkowaniu dla warunków brzegowych
![]()
i dla grubości filmu olejowego określonego związkiem
![]()
otrzymujemy rozkład ciśnienia
![]()
oraz nieznany parametr ![]()
![]()
Znając ciśnienie możemy obliczyć siłę działającą na górną płytkę
![]()
gdzie współczynnik siły nośnej jest określony wzorem:
Różniczkując wyrażenie dla składowej prędkości (8.59a) obliczymy jeszcze na-prężenie styczne
![]()
i siłę tarcia działającą na płytkę
![]()
250