[tabelkę pozostawiam Twojej inwencji, jeśli chcesz logo polibudy też możesz przerysować]

	Marek Oleksiewicz Katarzyna Sach	Wydział: elektryczny Rok: drugi Grupa: I Rok Akademicki 1999/2000
LABORATORIUM FIZYKI
Data ćwiczenia: 13.10.99 [?] Nr ćwiczenia: [wstaw]	Temat: [przepisz]	Ocena: [jak chcesz to też wstaw]

Cel ćwiczenia

Zbadanie prędkości rozchodzenia się fal dźwiękowych w powietrzu od ich częstotliwości.

Omówienie tematu

Falami dźwiękowymi, nazywamy podłużne fale mechaniczne, mogące rozchodzić się w ciałach stałych, cieczach i gazach. Materialne cząstki ośrodka, w którym rozchodzi się fala dźwiękowa, drgają wzdłuż prostej rozchodzenia się fali.

Źródłem dźwięku jest każde urządzenie, które drgając powoduje okresowy, falowy ruch powietrza. Elementy drgające periodycznie zagęszczają i rozrzedzają otaczające je powietrze. W granicach częstotliwości od 20 Hz do 20 kHz fale te są słyszalne i nazywamy akustycznymi. Drgania o wyższej częstotliwości nazywamy ultradźwiękami, a o niższej infradźwiękami.

Prędkość dźwięku w powietrzu zależy od jego temperatury, ponieważ wraz z temperaturą zmienia się gęstość powietrza. Zależność tę wyraża się wzorem:

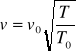
gdzie T₀=273,16 K, v₀- prędkość dźwięku w temperaturze T0

dla temperatury przy której wykonano pomiar:

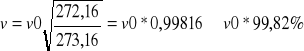
Błąd względny związany z temperaturą wynosi więc 0,18%. Ponieważ jest to wartość o rząd mniejsza niż błędy nieczułości, nie został uwzględniony w obliczeniach.

Fala charakteryzują się określoną częstotliwością f , która jest wielkością odwrotną do okresu. Fala w ciągu jednego okresu przebywa drogę , stąd prędkość rozprzestrzeniania się wynosi:

gdzie: - długość fali

T - okres drgań

f - częstotliwość drgań

Układ pomiarowy

[przerysuj ze skryptu]

Układ złożony jest z generatora dźwięku (ze wzmacniaczem), głośnika, mikrofonu oraz oscyloskopu. Układ pozwala na wytworzenie fal elektrycznych przesuniętych w fazie, których złożenie jest obserwowane na oscyloskopie. Do toru X oscyloskopu przykładamy napięcie bezpośrednio z generatora. Do toru Y sygnał dociera przez wzmacniacz, głośniki mikrofon, jest więc opóźniony w fazie w stosunku do sygnału toru X. W zależności od odległości pomiędzy mikrofonem a głośnikiem zmienia się przesunięcie fazowe (także amplituda, ale nie ma wpływu na wynik pomiaru) między sygnałami i na ekranie oscyloskopu otrzymujemy odpowiadające im krzywe Lissajous.

Przesunięciu mikrofonu z położenia z₁ do położenia z₂ towarzyszy zmiana fazy:

Zmieniając odległość między głośnikiem a mikrofonem i obserwując przejście krzywej Lissajous na oscyloskopie o 2 możemy określić wielkość . Znając częstotliwość drgań (odczytujemy z miernika częstotliwości) możemy wyznaczyć prędkość fali

gdzie : z₂ - z₁ = k k- liczba całkowita (ilość przejść o 2)

Wyniki pomiarów

Tabela 1

częstotliwość 1kHz

ze względu na duży błąd nieczułości związany z kształtem krzywej na oscyloskopie, pomiar nie został wykonany

Tabela 2

częstotliwość 2kHz ^*1
lp	zmierzona wartość [mm]	błąd nieczułości [mm]	liczba zmierzonych okresów (k)
	187	2	1
	165	2	1
średnia	176
v=352 [m/s] V=4 [m/s] - błąd bezwzględny wynikający z nieczułości oscyloskopu δV=1,14% - błąd względny wynikający z nieczułości oscyloskopu

*1 - ze względu na niewielką liczbę pomiarów, niepewność wyniku należy uznać za znacznie wyższą niż wynika to z błędu nieczułości. Wynosi ona nie mniej niż:

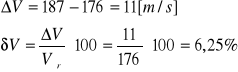
Tabela 3

częstotliwość 5kHz
lp	zmierzona wartość [mm]	błąd nieczułości [mm]	liczba zmierzonych okresów (k)		błąd bezwzględny
	73	3	1		0,33
	72	3	1		-0,67
	73	3	1		0,33
*1	136	3	1		-
*1	87	3	1		-
średnia	72,67			błąd średni kwadratowy	0,6
v=364 [m/s] V=15 [m/s] δV=4,1%

*1 - wynik został uznany za błędny i nie został uwzględniony przy obliczeniach

Przykład obliczeń:

Tabela 4

częstotliwość 7,5kHz

pomiar został uznany za błędny

Tabela 5

częstotliwość 10kHz
lp	zmierzona wartość [mm]	błąd nieczułości [mm]	liczba zmierzonych okresów (k)		błąd bezwzględny
	37	2	1		0,5
	36	2	1		-0,5
	36	2	1		-0,5
	36	2	1		-0,5
	36	2	1		-0,5
	36	2	1		-0,5
	35	2	1		-1,5
	37	2	1		0,5
	42	2	1		5,5
	34	2	1		-2,5
średnia	36,5			błąd średni kwadratowy	2,12
v=365 [m/s] V=20 [m/s] δV=5,5%

Tabela 6

częstotliwość 12,5kHz
lp	zmierzona wartość [mm]	błąd nieczułości [mm]	liczba zmierzonych okresów (k)		błąd bezwzględny
	30	3	1		0,64
	28	3	1		-1,36
	30	3	1		0,64
	30	3	1		0,64
	29	3	1		-0,36
	32	3	1		2,64
	28	3	1		-1,36
	25	3	1		-4,36
	29	3	1		-0,36
	30	3	1		0,64
	32	3	1		2,64
średnia	1			błąd średni kwadratowy	1,96
v=367 [m/s] V=38 [m/s] δV=10,3%

Tabela 7

częstotliwość 15kHz
lp	zmierzona wartość [mm]	błąd nieczułości [mm]	liczba zmierzonych okresów (k)	błąd bezwzględny
	24	2	1	0,43
	24	2	1	0,43
	23	2	1	-0,57
	25	2	1	1,43
	23	2	1	-0,57
	24	2	1	0,43
	22	2	1	-1,57
średnia	2		błąd średni kwadratowy	0,98
v=354 [m/s] V=30 [m/s] δV=8,5%

Tabela 8

częstotliwość 20kHz

ze względu na duży błąd nieczułości pomiar dla tej częstotliwości nie został wykonany

wyniki pomiarów

[tu narysuj wykres]

Na postawie wykonanych pomiarów, możemy stwierdzić, że prędkość dźwięku w powietrzu jest zależna od częstotliwości fali, dla której wykonujemy pomiar. Wraz ze wzrostem częstotliwości prędkość dźwięku wykazuje tendencję wzrostową. Ze względu na dużą niepewność pomiaru (przekraczającą dla niektórych częstotliwości 10%) kształtu krzywej prędkości w funkcji częstotliwości nie zdołaliśmy ustalić. Nie możemy więc określić, czy jest ona liniowa, czy przybiera inny kształt.

Cz. Bobrowski „Fizyka- krótki kurs”. Wartości przybliżone, w rzeczywistości zakres słyszalny jest cechą indywidualną i zwykle odbiega od tych wartości

Opóźnienie fali elektromagnetycznej, czas propagacji sygnału na oscyloskopie oraz opóźnienie wprowadzane przez wzmacniacz sygnału pomijamy, jako znikomo małe i mające bardzo niewielki wpływ na dokładność pomiaru.

Pomiary zostały wykonane w warunkach:

• temperatura: 19 ⁰C

• ciśnienie: 1025 hPa

---