LOGISTYKA I ROK	Beata Kozłowska grupa L3		12.03.2009
	15. Zjawisko Halla	Ocena

1. Wprowadzenie

1. Zjawisko Halla - zjawisko powstania różnicy potencjałów U pomiędzy przeciwległymi ściankami półprzewodnika lub metalu w kierunku prostopadłym zarówno do kierunku przepływu prądu I, jak i do kierunku wektora indukcji zewnętrznego pola magnetycznego B. Jest jednym z najważniejszych zjawisk, które występują w metalach i półprzewodnikach. Pojawienie się napięcia Halla wynika z faktu, że pole magnetyczne powoduje ruch nośników prądu po torach zakrzywionych.

2. Napięcie Halla - pojawiająca się różnica potencjałów U_H

3. Hallotrony - półprzewodniki służące do pomiaru indukcji B wykorzystujące zjawisko Halla.

4. Na ładunek elektryczny
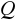
   poruszający się z prędkością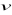
   w polu magnetycznym o indukcji B, działa siłą Lorentza:

gdzie
- indukcja magnetyczna.

Kierunek tej siły zależy od znaku nośników ładunku
oraz iloczynu wektorowego prędkości
i indukcji B. jeśli prędkość nośników ładunku ma składową prostopadłą do indukcji B, to pod działaniem siły Lorentza następuje odchylenie nośników ładunku w kierunku prostopadłym do
i B. w wyniku tego następuje przestrzenne rozdzielenie ładunków i pojawia się pole elektryczne E_H.

5. Pod działaniem siły Lorentza przy ustalonym przez nas kierunku B i E, dziury w półprzewodniku akceptorowym i elektrony w półprzewodniku donorowym odchylają się ku górnej ściance próbki, a na dolnej ściance występuje niedostatek odpowiednich nośników ładunku, co powoduje powstanie przeciwnego co do znaku ładunku w stosunku do ładunku na górnej ścianie. Ten proces trwa do momentu, kiedy to powstające w wyniku rozdzielenia nośników ładunku poprzeczne pole elektryczne E_H nie wytworzy siły działającej na swobodne nośniki ładunku równoważącej siłę Lorentza

6. Napięcie Halla obliczamy ze wzoru:

gdzie R_H =
[m³/As]

R_H - stała Halla,

I
- natężenie prądu płynącego przez próbkę,

B - indukcja magnetyczna,

d - grubość próbki.

7. W tym ćwiczeniu używamy cienkowarstwowego hallotronu wykonanego z antymonku indu InSb

2. Tabela pomiarów

Natężenie prądu magnesującego IM[A]	Wartość indukcji pola mag. B[T]	Natężenie prądu sterującego I[A]	Napięcie Halla		Średnia wartośc napięcia UH[V]
							UH1[V]	UH2[V]
		1,0	0,4	0,00	0,000	0,000	0,0000
				0,54	0,020	0,025	0,0225
				1,00	0,036	0,044	0,0400
				1,50	0,054	0,065	0,0595
				2,00	0,072	0,086	0,0790
				2,50	0,089	0,107	0,0980
				3,00	0,108	0,128	0,1180
				3,50	0,126	0,150	0,1380
				4,00	0,143	0,170	0,1565
				4,50	0,160	0,191	0,1755
				5,00	0,177	0,211	0,1940
		2,0	0,8	0,00	0,000	0,000	0,0000
				0,53	0,039	0,045	0,0420
				1,0	0,074	0,084	0,0790
				1,5	0,111	0,125	0,1180
				2,0	0,148	0,167	0,1575
				2,5	0,185	0,207	0,1960
				3,0	0,221	0,248	0,2345
				3,5	0,257	0,288	0,2725
				4,0	0,292	0,329	0,3105
				4,5	0,325	0,368	0,3465
				5,0	0,362	0,406	0,3840

3. Przebieg ćwiczenia

Łączymy wszystkie przyrządy używane w doświadczeniu według przedstawionych schematów. Sprawdzamy, czy potencjometr zasilacza regulowanego ustawiony jest w położenie I_min. Podobnie sprawdzamy ustawienie pokrętła autotransformatora . Włączamy zasilacz, mierniki i autotransformator do sieci. Hallotron umieszczamy miedzy biegunami elektromagnesu.

Przy włączonym przełączniku kierunkowym k, ustawiamy jedną z dwóch wartości prądy magnesującego I_M.

Przy niezmiennym położeniu hallotronu i ustalonej wartości I_M wykonujemy pomiary napięcia Halla U_H1, zmieniając natężenie prądu sterującego I co 0.5, w zakresie od 0 do 5 mA. Wyniki obserwacji zapisujemy w tabeli pomiarów.

Zmieniamy kierunek prądu magnesującego przełącznika K i przy tej samej co poprzednio wartości I_M wykonujemy pomiary U_H2.

Powtarzamy opisane czynności.

4. Obliczenia

Do obliczenia stałej Halla korzystamy ze wzoru:

Gdzie:

d - grubość płytki półprzewodnikowej która wynosi 8 ⋅ 10^-6 [m],

U_H - średnia wartość napięcia,

B - indukcja magnetyczna ,

I_x - prąd sterujący.

Do wyznaczenia koncentracji „n” nośników prądu używamy wzoru:

Gdzie:

R - stała Halla

e - ładunek elementarny elektronu:

a) dla: I_M = 1 [A]

B = 0,4 [T]

I_x
dla x=1,2, 3, ... , 10

U_Hx dla x=1,2, 3,... , 10

Przykładowe obliczanie stałej Halla (R):

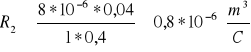
Przykładowe obliczanie koncentracji nośników ładunku (n):

Zestawienie otrzymanych wyników:

Lp.	R*10^-6	n*10^25
1.	0,83	0,75
2.	0,80	0,78
3.	0,79	0,79
4.	0,79	0,79
5.	0,78	0,80
6.	0,79	0,79
7.	0,79	0,79
8.	0,78	0,80
9.	0,78	0,80
10.	0,78	0,81
Wart. średnie	0,79	0,79

b) Dla: I_M= 2 [A]

B = 0,8 [T]

U_Hx dla x=1,2, 3, ... , 10

I_x dla x=1,2, 3, ... , 10

Przykładowe obliczanie stałej Halla (R):

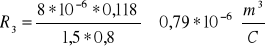
Przykładowe obliczanie koncentracji nośników ładunku (n):

Zestawienie otrzymanych wyników:

Lp.	R*10^-6	n*10^25
1.	0,79	0,79
2.	0,79	0,79
3.	0,79	0,79
4.	0,79	0,79
5.	0,78	0,80
6.	0,78	0,80
7.	0,78	0,80
8.	0,78	0,81
9.	0,77	0,81
10.	0,77	0,81
Wart. średnie	0,78	0,80

5. Niepewności pomiarów

Δd I_M [mA] = 0,04 [mA] ;

Δ _d I_x [mA] = 0,3 [mA]

Δ_d U = 0,05 * U

Δ_d I= 0,05 * I

Δ_d B = 0,05 * B

Odczytane wartości indukcji pola magnetycznego wynoszą:

a) B (I_M = 1A) = 0,4 [T] ;

b) B (I_M = 2A) = 0,8 [T] ;

gdzie przyjęty błąd odczytu : ΔB = 0,02 [T].

(skorzystaliśmy z zależności B[T]=0,4 I_M )

u(U)=0,05·U=0,05·0,0225=0,001125

u(U) dla IM=1,0	u(U) dla IM=2,0
0,0011	0,0021
0,0020	0,0039
0,0030	0,0059
0,0040	0,0079
0,0049	0,0098
0,0059	0,0117
0,0069	0,0136
0,0078	0,0155
0,0088	0,0173
0,0097	0,0192

Wartości średnie dla I_M=1,0 u(U)= 0,00541

dla I_M=2,0 u(U)= 0,01069

u(I)=0,05·I=0,05·0,54=0,027

u(I)
0,027
0,050
0,075
0,100
0,125
0,150
0,175
0,200
0,225
0,250

Wartość średnia u(I)= 0,1377

u(B)=0,05·B=0,05·0,40=0,020

u(B)=0,05·0,80=0,40

Obliczenie niepewności złożonej dla R i n

• Dla I_M=1

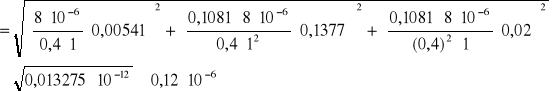
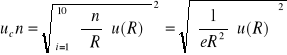
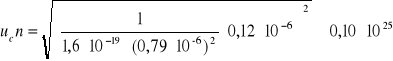
• Dla I_M=2

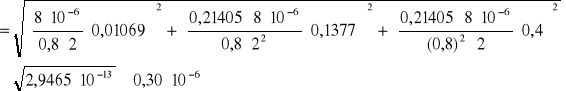
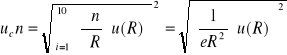
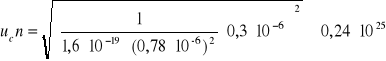
Zestawienie wyników:

	Dla IM=1,0	Dla IM=2,0
Stała Halla R	(0,79 ± 0,12)	(0,78 ± 0,30)
Koncentracja nośników prądu n	(0,79 ± 0,10) ·10^25	(0,80 ± 0,24) ·10^25

6. Wnioski

W ćwiczeniu wyznaczyliśmy stałą Halla oraz koncentrację nośników prądu.

Z naszych wykresów wynika, że zależność napięcia Halla od prądu sterowania jest „liniowo”, oraz, że wzrost prądu magnesowania powoduje wzrost stałej Halla, a co za tym idzie zmniejszenie się koncentracji nośników w badanym elemencie.

Po obliczeniu stałej Halla zauważyliśmy, że wartość ta maleje wraz z wzrostem natężenia prądu sterującego. Natomiast dla koncentracji nośników prądu n wartość rośnie. Niepewności pomiarów wynikały z niedokładności mierników.

---