II CZĘŚĆ PRAKTYCZNA:

1.Wprowadzenie.

Pomiar pośredni - to metoda pomiarowa, która umożliwia pomiar wielkości pośrednich, z pomiarów bezpośrednich innych wielkości związanych odpowiednio z wielkością mierzoną.

2.Przebieg ćwiczenia:

1.Pomiar pośredni promienia łuku przy użyciu mikroskopu pomiarowego.

Pomiaru tego dokonujemy przy pomocy mikroskopu warsztatowego małego (MWM). Rzeczywistym celem pomiaru jest promień łuku R, a my zmierzymy strzałkę s i odpowiadającą jej cięciwę c bezpośrednio, a następnie pośrednio przez wprowadzenie wzoru wyliczymy promień łuku R. Mierzony promień R jest zatem funkcją strzałki i cięciwy łuku.

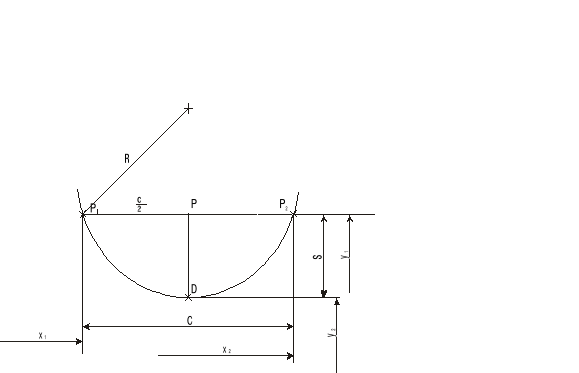
Rys.1. Sposób pomiaru strzałki s i cięciwy c za pomocą mikroskopu warsztatowego.

gdzie:

R - promień łuku;

c - cięciwa;

s - strzałka.

Pomiary wartości punktów A, B, C:

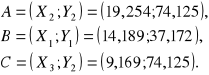
Obliczenie wartości cięciwy c, strzałki s i promienia R:

Obliczenie niepewności pomiarowej mikroskopu warsztatowego
:

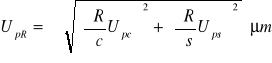
H- wysokość przedmiotu

H=0;

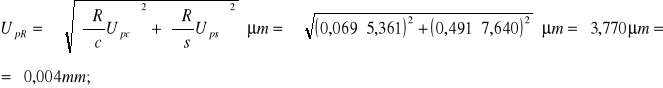
Wynik końcowy:

2. Pomiar łuku za pomocą wałeczków pomiarowych.

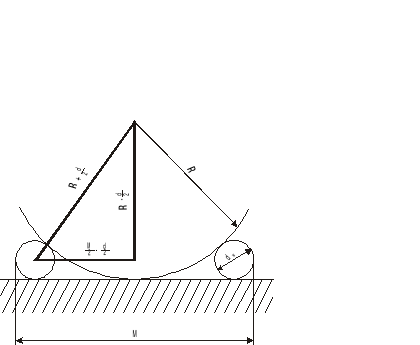
Jest to pomiar pośredni, wielkościami mierzonymi bezpośrednio są:

• wymiar M;

• średnica wałeczków d;

Promień łuku R oblicza się ze przy pomocy tych dwóch wielkości.

gdzie:

R - promień łuku;

d - średnica wałeczków;

M - wymiar mierzony.

Przebieg ćwiczenia:

Najpierw odczytujemy średnicę pierwszej pary wałeczków d₁ = 20,002 mm, to samo robimy dla drugiej pary d₂ = 29,995.

Pomiar I

Średnica wałeczka pomiarowego: d_w = 29,995mm

Wielkość mierzona: M₁ = 172,615mm

Promień łuku:

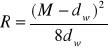
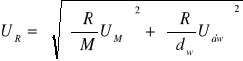
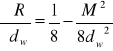
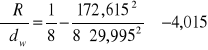
R = 81,73 ± 0,012 mm

Pomiar II

Średnica wałeczka pomiarowego: d_w = 20,002mm

Wielkość mierzona: M₂ = 115,965mm

Promień łuku:

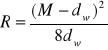
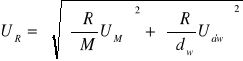
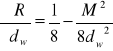
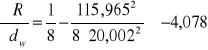
R = 57,43 ± 0,012 mm

Wydział Budowy Maszyn i Informatyki Bielsko - Biała, 16.03.2010

Rok akademicki: 2009/2010

Studia: stacjonarne/inż.

Semestr: 4

Kierunek/Specjalność: ZiIP

Grupa: Wtorek - godz. 14.15-16.00

LABORATORIUM

METROLOGII TECHNICZNEJ

Laboratorium nr 5

Niepewność pomiaru w pomiarach pośrednich

część II

Wykonala:

Sprawozdanie
Do poprawy:
Zaliczone:

I CZĘŚĆ TEORETYCZNA

NIEPEWNOŚĆ POMIARU W POMIARACH POŚREDNICH

Celem kolejnych ćwiczeń w laboratorium metrologii było przypomnienie podstawowych pojęć związanych z niepewnością pomiaru, omówienie zależności, że pomiar jest dwuelementowy oraz stwierdzenia mówiącego, że niepewność pomiaru zależy od strategii pomiaru. Oprócz samego wyjaśnienia tych zależności przedstawiono wyznaczenie złożonej niepewności pomiaru w pomiarach pośrednich, tym samym sposób posługiwania się przyrządami mikrometrycznymi, odczytywanie wskazań przez interpolację z dokładnością 0,001 mm przez dobór odpowiednich końcówek pomiarowych i wymiana trzpieni pomiarowych w głębokościomierzu.

NIEPEWNOŚĆ STANDARDOWA POMIARÓW POŚREDNICH

Z pomiarami pośrednimi mamy do czynienia, gdy dokonuje się pomiarów bezpośrednich kilku wielkości x1, x2, …,xk , a następnie na ich podstawie wyznacza wielkość y określoną przez związek funkcyjny:

y = f(x1, x2, …, xk)

Metody określania niepewności pomiarowych:

• Niepewność standardowa pomiarów bezpośrednich

Przypuśćmy, że wykonaliśmy serię n pomiarów bezpośrednich wielkości fizycznej X otrzymując wyniki X₁, X₂ ...X_n. Jeśli wyniki pomiarów nie są takie same, wówczas za najbardziej zbliżoną do wartości prawdziwej przyjmujemy średnią arytmetyczną ze wszystkich wyników pomiarów:

(1)

Stwierdzenie to jest tym bardziej słuszne im większa jest liczba przeprowadzonych pomiarów (dla
,
). W celu określenia niepewności standardowej posługujemy się w tym wypadku sposobem typu A, czyli korzystamy ze wzoru na odchylenie standardowe średniej

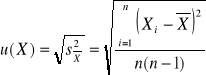
(2)

Jeśli natomiast wyniki pomiarów nie wykazują rozrzutu, czyli
, lub też gdy istnieje tylko jeden wynik pomiaru, wówczas niepewność standardową szacujemy sposobem typu B. Można np. wykorzystać informację o niepewności maksymalnej
określonej przez producenta przyrządu pomiarowego, jeśli nie mamy innych dodatkowych informacji, wówczas niepewność standardową obliczamy ze wzoru

(3)

Dla prostych przyrządów (tj. linijka, śruba mikrometryczna czy termometr) jako
można przyjąć działkę elementarną przyrządu. W elektronicznych przyrządach cyfrowych niepewność maksymalna podawana jest przez producenta w instrukcji obsługi i jest zwykle kilkakrotnie większa od działki elementarnej. Najczęściej zależy ona od wielkości mierzonej X i zakresu na którym mierzymy Z:

Gdy występują oba typy niepewności (tzn. zarówno rozrzut wyników jak i niepewność wzorcowania) i żadna z nich nie może być zaniedbana (tzn. obie są tego samego rzędu), wówczas niepewność standardową (całkowitą) obliczamy ze wzoru

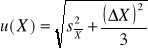
. (4)

• Niepewność standardowa pomiarów pośrednich - niepewność złożona (u_c)

W przypadku pomiarów pośrednich wielkość mierzoną Y obliczamy korzystając ze związku funkcyjnego, który można zapisać w ogólnej postaci:
, gdzie symbolami
oznaczamy k wielkości fizycznych mierzonych bezpośrednio. Zakładamy, że znane są wyniki pomiarów tych wielkości
oraz ich niepewności standardowe
. Wynik (końcowy) pomiaru oblicza się wówczas ze wzoru:

W przypadku pomiarów pośrednich nieskorelowanych (tzn. gdy każdą z wielkości
mierzy się niezależnie) niepewność złożoną wielkości Y szacujemy przy pomocy przybliżonego wzoru:

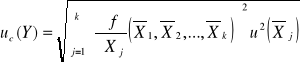
(5)

• Niepewność rozszerzona

Niepewność standardowa całkowicie i jednoznacznie określa wartość wyniku, jednak do wnioskowania o zgodności wyniku pomiaru z innymi rezultatami (np. z wartością tabelaryczną) oraz dla celów komercyjnych i do ustalania norm przemysłowych, zdrowia, bezpieczeństwa itp. Międzynarodowa Norma wprowadza pojęcie niepewności rozszerzonej oznaczanej symbolem U (dla pomiarów bezpośrednich), lub U_c (dla pomiarów pośrednich). Wartość niepewności rozszerzonej oblicza się ze wzoru

lub
(6)

Liczba k, zwana współczynnikiem rozszerzenia, jest umownie przyjętą liczbą wybraną tak, aby w przedziale
znalazła się większość wyników pomiaru potrzebna dla danych zastosowań. Wartość współczynnika rozszerzenia mieści się najczęściej w przedziale 2-3. W większości zastosowań zaleca się przyjmowanie umownej wartości
.

Wałeczki pomiarowe - są wzorcami końcowymi, które średnice odtwarzają wzorcowe wymiary. Znajdują zastosowanie w pomiarach średnic podziałowych gwintów zewnętrznych, niektórych parametrów kół zębatych, kątów stożków zewnętrznych, promieni łuków, itp. Komplet wałeczków pomiarowych do gwintów stanowi 21 trójek wałeczków o średnicach od 0,17 do 6,35 mm.

Produkuje się również wałeczki do pomiaru kół zębatych. Komplet stanowią 23 pary wałeczków o wymiarach Pd 1-7 do 17 mm.

6

---