Ćwiczenie nr 5
Pomiary impedancji
Cel ćwiczenia :
Celem ćwiczenia jest przyswojenie pojęcia impedancji; pomiar impedancji elementów RLC, poznanie sposobu definiowania parametrów elementów RLC w oparciu o składowe impedancji; pomiar parametrów elementów RLC w funkcji częstotliwości.
Przyrządy pomiarowe :
Mikroprocesorowy miernik impedancji 3532 HIOKI
Automatic C Bridge TYPE E 315A
Obiekty pomiaru :
Elementy bierne : kondensatory, rezystory, cewki indukcyjne
Schematy zastępcze dla elementów rzeczywistych :
Rys.1) Schemat zastępczy dla kondensatora
Rys.2) Schemat zastępczy dla cewki powietrznej i rezystora
Pomiary :
Pomiar impedancji wybranego elementu - kondensator 0,047 ηF 400V.
Do pomiarów wykorzystaliśmy miernik impedancji 3532 HIOKI.
Impedancja Z = 3,56 kΩ
Przesunięcie fazowe φ = -89,6°
Błąd względny pomiaru impedancji :
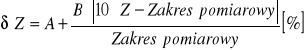
Zakres pomiarowy (RANGE) = 10 kΩ
Wartości A i B zależą od częstotliwości pomiaru, poziomu sygnału pomiarowego oraz zakresu. Wartości te zostały odczytane z tabeli w instrukcji :
A= 0,08
B= 0,01
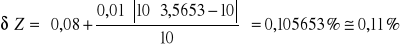
Przesunięcie fazowe w badanym kondensatorze wyniosło φ = -89,6° ,co dowodzi, że ten element nie spełnia tylko i wyłącznie roli pojemności (nie jest elementem idealnym, wyidealizowanym, czyli bezstratnym), ale także pojawiają się w nim straty spowodowane rezystancją doprowadzeń i strat dielektrycznych. Mimo to wartość przesunięcia fazowego nie odbiega znacznie od ![]()
, co świadczy o pojemnościowym charakterze badanego elementu. W zakresie małych częstotliwości należy kondensator traktować jako dwójnik o elementach: rezystancyjnym i pojemnościowym, połączonych szeregowo lub równolegle. Błąd względny pomiaru impedancji utrzymał się na bardzo niskim poziomie, co świadczy, że metoda ta doskonale nadaje się do tego typu pomiaru.
Pomiar parametrów szeregowego i równoległego układu zastępczego :
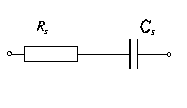
Schemat szeregowy i równoległy oraz wartości :
Rs=23,7[Ω]
Cs=44,6[nF]
Rp=537,4[kΩ]
Cp=44,6[nF]
Wyniki pomiaru pojemności okazały się stosunkowo dokładne (rzeczywista wartość 47[nF],ta z pomiarów 44,6[nF]).
Pomiar parametrów kondensatorów :
Pomiar Cs, Cp, Rs, Rp w funkcji częstotliwości :
L.p. |
f [kHz] |
Cs [nF] |
Rs [Ω] |
Cp [nF] |
Rp [Ω] |
D |
1 |
0,05 |
44,9 |
87,5 |
44,8 |
56112000,0 |
0,05 |
2 |
10,00 |
44,3 |
4,7 |
44,2 |
27591,0 |
0,05 |
3 |
100,00 |
43,6 |
1,5 |
43,5 |
866,6 |
0,05 |
4 |
200,00 |
43,4 |
1,3 |
43,2 |
257,3 |
0,07 |
5 |
300,00 |
43,5 |
1,2 |
43,1 |
123,1 |
0,10 |
6 |
500,00 |
44,2 |
1,1 |
43,1 |
46,6 |
0,16 |
7 |
700,00 |
45,3 |
1,1 |
43,3 |
24,0 |
0,21 |
8 |
900,00 |
47,1 |
1,1 |
43,6 |
14,2 |
0,28 |
9 |
1000,00 |
48,3 |
1,1 |
43,8 |
11,3 |
0,32 |
Tabela pomiarowa nr 1
Oznaczenia :
f - częstotliwość [kHz]
Cs, Rs - pojemność i rezystancja w szeregowym układzie zastępczym [nF, Ω]
Cp, Rp - pojemność i rezystancja w równoległym układzie zastępczym
D - współczynnik strat kondensatora
Przykładowe obliczenia współczynnika strat kondensatora :
Dla pomiaru nr 6:
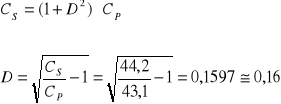
Wykres nr 1
W miarę wzrostu częstotliwości rezystancja pasożytnicza, na którą składają się : rezystancja doprowadzeń, elektrod, strat dielektrycznych dielektrycznych upływności doprowadzeń, w dość szybkim tempie malała. Pojemność kondensatora praktycznie pozostawała bez zmian, stąd wniosek, że tylko nieznacznie zależy od częstotliwości.
Na podstawie następnego wykresu łatwo zauważyć, że współczynnik stratności powoli rośnie wraz ze wzrostem częstotliwości. Przy częstotliwości 1MHZ osiąga wartość 0,32.
Wykres nr 2
Procentowa zmiana pojemności kondensatora w funkcji częstotliwości :
Jako pojemność odniesienia przyjąłem wyniki pomiaru przy częstotliwości 1 kHz.
|
|
|
|
Procentowa zmiana pojemności [%] |
|
L.p. |
f [kHz] |
Cs [nF] |
CP [nF] |
Cs |
CP |
1 |
1 |
44,6 |
44,6 |
|
|
2 |
0,05 |
44,9 |
44,8 |
0,7 |
0,4 |
3 |
10,00 |
44,3 |
44,2 |
0,7 |
0,9 |
4 |
100,00 |
43,6 |
43,5 |
2,2 |
2,5 |
5 |
200,00 |
43,4 |
43,2 |
2,7 |
3,1 |
6 |
300,00 |
43,5 |
43,1 |
2,5 |
3,4 |
7 |
500,00 |
44,2 |
43,1 |
0,9 |
3,4 |
8 |
700,00 |
45,3 |
43,3 |
1,6 |
2,9 |
9 |
900,00 |
47,1 |
43,6 |
5,6 |
2,2 |
10 |
1000,00 |
48,3 |
43,8 |
8,3 |
1,8 |
Tabela pomiarowa nr 2
Pojemności w układzie szeregowym różnią się od pojemności odniesienia (dla 1kHz) o (0,7% - 8,3%),natomiast w układzie równoległym o (0,4% - 3,4%). O ile w układzie równoległym trudno jest mówić o jakichś znaczących zmianach pojemności przy zmianie częstotliwości, to w układzie szeregowym dla częstotliwości 900 [kHz]- 1000 [kHz] wyniki pomiaru dość znacznie (5,6% - 8,3%) odbiegają od wartości wzorcowych.
Pomiar parametrów rezystora
- rezystor czerwony 68 kΩ
Pomiar impedancji Z oraz przesunięcia fazowego φ w funkcji częstotliwości :
L.p. |
f [kHz] |
Z [kΩ] |
φ[°] |
1 |
0,05 |
68,6 |
-0,14 |
2 |
10,00 |
68,6 |
-0,03 |
3 |
100,00 |
68,5 |
-0,94 |
4 |
200,00 |
68,5 |
-1,77 |
5 |
300,00 |
68,6 |
-2,64 |
6 |
500,00 |
68,3 |
-4,47 |
7 |
700,00 |
67,9 |
-6,24 |
8 |
900,00 |
67,6 |
-7,96 |
9 |
1000,00 |
67,4 |
-8,84 |
Tabela pomiarowa nr 3
Oznaczenia :
f - częstotliwość [kHz]
Z -impedancja [kΩ]
Φ - przesunięcie fazowe [°]
W miarę wzrostu częstotliwości coraz wyraźniejszy staję się pojemnościowy charakter tego rezystora. Idealny rezystor nie wprowadza przesunięcia fazowego (φ=0°), tutaj jednak przesunięcie to staję się coraz bardziej zauważalne (wzrasta jego ujemna wartość, czyli napięcie opóźnia się w stosunku do prądu, przyjmuje charakter pojemnościowy). Wpływ ma tutaj pojemność pasożytnicza CP, która w schemacie zastępczym podłączona jest równolegle do rezystora RP.
Schemat zastępczy o charakterze pojemnościowym
W przedziale częstotliwości ![]()
impedancja rezystora nie zmienia się o więcej niż o 0,5%. Na pomiary niższych częstotliwości nie pozwalały ograniczenia miernika.
Dla 50 [Hz] impedancja wynosi Z = 68,6 [kΩ], 0,5 % tej wartości to w przybliżeniu 0,34 [kΩ], więc przedział wartości impedancji to ![]()
.
Dla 42 [Hz] RP = 68,6 [kΩ] ,CP = 171,9 [pF]
Dla 545 [kHz] RP = 68,5 [kΩ] ,CP = 0,36 [pF]
Rezystancja kondensatora dla schematu równoległego nie zmienia się o więcej niż o 5% dla częstotliwości ![]()
.
Dla 545 [kHz] RP = 68,5 [kΩ], a 5% z tej wartości to w przybliżeniu 3,4 [kΩ]
Dla częstotliwości z powyższego przedziału wartości rezystancji mieszczą się w przedziale![]()
Dla 545 [kHz] CP = 0,36 [pF], a 5% z tej wartości to w przybliżeniu 0,02[pF]
Nie udało się jednak określić dokładnego przedziału wartości częstotliwości, dla których pojemność mieściłaby się w przedziale ![]()
.
Pomiar parametrów cewek
- cewka 10/1.5
Pomiar indukcyjności Ls, Lp oraz rezystancji Rs, Rp cewki w szeregowym i równoległym układzie zastępczym w funkcji częstotliwości.
L.p. |
f [kHz] |
Ω[Hz] |
Ls [µH] |
Rs [mΩ] |
Q |
Lp [µH] |
Rp [mΩ] |
Q |
1 |
0,05 |
314 |
12,6 |
89,6 |
0,04 |
6,4 |
89,4 |
0,02 |
2 |
10,00 |
62800 |
11,9 |
89 |
8,4 |
12,1 |
6,4 |
118,7 |
3 |
100,00 |
628000 |
11,9 |
165,7 |
45,1 |
11,9 |
339,8 |
22,0 |
4 |
200,00 |
1256000 |
11,9 |
334,3 |
44,7 |
11,9 |
667,6 |
22,4 |
5 |
300,00 |
1884000 |
11,8 |
556,2 |
40,0 |
11,8 |
892,8 |
24,9 |
6 |
500,00 |
3140000 |
11,7 |
1,3 |
28260,0 |
11,7 |
1,3 |
28260,0 |
7 |
700,00 |
4396000 |
11,6 |
1,6 |
31871,0 |
11,6 |
1,6 |
31871,0 |
8 |
900,00 |
5652000 |
11,5 |
2 |
32499,0 |
11,5 |
2,1 |
30951,4 |
9 |
1000,00 |
6280000 |
11,5 |
2,2 |
32827,3 |
11,5 |
2,4 |
30091,7 |
Tabela pomiarowa nr 4
Oznaczenia :
ω - częstość kołowa [Hz]
LS,P - indukcyjność [µH]
RS,P - rezystancja [mΩ]
Q - dobroć cewki
Przykładowe obliczenia współczynnika dobroci cewki Q :
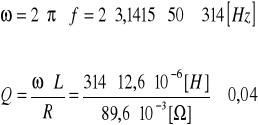
Pomiary, a tym samym odczyt dokładnych wartości był w tym przypadku utrudniony, ponieważ wartości poszczególnych parametrów (szczególnie rezystancji) pojawiające się na wyświetlaczu miernika zmieniały się w bardzo szybkim tempie, trudno było określić stabilny i ostateczny wynik. Widać na podstawie tabeli bardzo dokładnie, że dobroć (parametr określający jakość cewki) wzrastała wraz ze wzrostem częstotliwości. Jej wartość w głównej mierze zależy od stosunku indukcyjności do rezystancji strat. Dobroć jest tym mniejsza, im większe są straty energii w cewce, a więc zależy od rodzaju przewodu, częstotliwości pracy itp. Straty energii wywołane są przez prądy wirowe oraz zjawisko naskórkowości.
W przedziale częstotliwości ![]()
dobroć cewki utrzymywała się na dość niskim poziomie, od kilku do kilkudziesięciu, natomiast powyżej tych częstotliwości gwałtownie wzrosła (rezystancja strat mocno zmalała).
Przypuszczalnie popełniliśmy przeoczenie przy odczycie jednostki (rezystancja wzrosła, a nie zmalała), w jakiej podawane były rezystancje w przedziale częstotliwości ![]()
. Byłoby to najbardziej prawdopodobne wyjaśnienie zawyżonych wyników, jakie otrzymaliśmy przy obliczaniu dobroci cewki. Poprawiona tabelka znajduje się poniżej.
L.p. |
f [kHz] |
ω |
Ls [µH] |
Rs [mΩ] |
Q |
Lp [µH] |
Rp [mΩ] |
Q |
6 |
500 |
3141592 |
11,7 |
1300 |
28,3 |
11,7 |
1300 |
28,3 |
7 |
700 |
4398229 |
11,6 |
1600 |
31,9 |
11,6 |
1600 |
31,9 |
8 |
900 |
5654866 |
11,5 |
2000 |
32,5 |
11,5 |
2100 |
31,0 |
9 |
1000 |
6283184 |
11,5 |
2200 |
32,8 |
11,5 |
2400 |
30,1 |
Tabela pomiarowa nr 5
Wykres nr 3
Procentowa zmiana indukcyjności cewki w funkcji częstotliwości:
Jako indukcyjność odniesienia przyjąłem wyniki pomiaru przy częstotliwości 1 kHz.
|
|
|
|
Procentowa zmiana indukcyjności [%] |
|
L.p. |
f [kHz] |
Ls [µH] |
Lp [µH] |
Ls |
Lp |
1 |
1,00 |
12,0 |
28,6 |
|
|
2 |
0,05 |
12,6 |
6,4 |
5,0 |
77,6 |
3 |
10,00 |
11,9 |
12,1 |
0,8 |
57,7 |
4 |
100,00 |
11,9 |
11,9 |
0,8 |
58,4 |
5 |
200,00 |
11,9 |
11,9 |
0,8 |
58,4 |
6 |
300,00 |
11,8 |
11,8 |
1,7 |
58,7 |
7 |
500,00 |
11,7 |
11,7 |
2,5 |
59,1 |
8 |
700,00 |
11,6 |
11,6 |
3,3 |
59,4 |
9 |
900,00 |
11,5 |
11,5 |
4,2 |
59,8 |
10 |
1000,00 |
11,5 |
11,5 |
4,2 |
59,8 |
Tabela pomiarowa nr 6
Indukcyjność w układzie szeregowym różni się od indukcyjności odniesienia o stosunkowo niewielką wartość (max. 0,6 [µH]), co odpowiada około 5 procentowej zmianie. Natomiast w układzie równoległym rozbieżności są już ogromne (max. 22,2 [µH]), co odpowiada około 78 procentowej zmianie wartości w stosunku do wzorca. Rozbieżność ta mogła być spowodowana błędem odczytu indukcyjności dla 1 [kHz], czyli naszego wzorca.
Pomiar parametrów kondensatora za pomocą mostka E315A :
- Wykonano pomiar dla czerwonego kondensatora 0,047 [µF]
- Wartości odczytane :
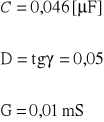
Wnioski i uwagi końcowe :
Wnioski do wykonywanych pomiarów zostały już po części zawarte przy poszczególnych punktach pomiarów.
Jeśli chodzi o wyniki to najbardziej zaskakujące były te dla cewki, prawdopodobnie popełniliśmy jakieś błędy przy pomiarze, wskazują na to dość nierealne i zawyżone wartości współczynnika dobroci Q, spodziewaliśmy się otrzymać wyniki na poziomie od kilku do kilkudziesięciu dla cewek o małej dobroci, od kilkudziesięciu do około dwustu dla cewki o średniej dobroci, ale wyniki dla częstotliwości ![]()
są znacznie zawyżone. Możemy tylko przypuszczać, że jednostka rezystancji (mΩ,Ω) została w tym przypadku źle odczytana z ekranu miernika. Decydujący wpływ miała tu rezystancja strat, im większa była tym mniejsza dobroć i odwrotnie. Trudno jest także określić częstotliwość rezonansową, ponieważ dobroć ma na nią spory wpływ (mała dobroć - krzywa rezonansowa jest spłaszczona).
Większość pomiarów przeprowadzona była z wykorzystaniem mikroprocesorowego miernika impedancji, 3532 HIOKI, dlatego o drugim (Automatic C Bridge TYPE E 315A) z urządzeń pomiarowych niewiele da się powiedzieć czy ocenić jego dokładność, która zależała od zastosowanego wzorca. Natomiast dokładność pierwszego z nich jest na bardzo wysokim poziomie, błąd względny pomiaru nie przekroczył wartości 1 %.
Pomiar parametrów kondensatora pokazuje, że przy niewielkich częstotliwościach istnieje tam dość znaczna rezystancja pasożytnicza, która w miarę wzrostu częstotliwości traci na znaczeniu (przy 1 [MHz] wynosi już tylko około 1,1[Ω]). Powoli natomiast rośnie wartość współczynnika stratności D.
W miarę wzrostu częstotliwości pracy rezystora coraz wyraźniejszy staję się jego pojemnościowy charakter. Idealny rezystor nie wprowadza przesunięcia fazowego (φ=0°), w rzeczywistym elemencie ta wartość dość znacznie wzrosła (czyli napięcie opóźnia się w stosunku do prądu).
Wyszukiwarka