Statystyka - wykład 1

(18 lutego'09)

STATYSTYKA - nauka o metodach ilościowych badania prawidłowości (procesów masowych). Przez zjawisko masowe należy rozumieć takie zjawisko, które badane w danej masie zdarzeń wykazuje właściwą sobie prawidłowość, jakiej nie można zaobserwować w pojedynczym przypadku (przykłady zjawisk masowych: liczba zgonów, urodzenia ludności, wielkość produkcji).

Przedmiotem badań statystycznych są określone zbiorowości statystyczne (populacje), które stanowią zbiór elementów (jednostek) powiązanych ze sobą logicznie (tzn. posiadających pewne cechy stałe) i jednocześnie nieidentycznych, np. zbiorowości nie będące statystycznymi: zbiór kul o tej samej średnicy, tego samego koloru - identyczne - mają tylko cechy wspólne, zbiór pocisków danego typu; zbiorowości statystyczne: studenci, zakłady należące do danej gałęzi przemysłu).

Rozróżnić można 2 rodzaje zbiorowości, a mianowicie zbiorowość generalna, którą stanowi zbiór elementów obejmujący wszystkie elementy będące przedmiotem badań oraz zbiorowość próbna (próbka), która jest podzbiorem zbiorowości generalnej obejmującej część jej elementów wybranych w określony sposób. W tym przypadku wyniki uzyskane w rezultacie badania podzbioru staramy się uogólnić na zbiorowość statystyczną.

Badania całej zbiorowości generalnej są w praktyce prowadzone stosunkowo rzadko. Wynika to głównie z następujących przyczyn:

1. prowadzone badanie niszczy jednostki zbiorowości generalnej

2. w wielu przypadkach badanie całej zbiorowości jest kapitało i czasochłonne i stąd nie każdy badacz ma możliwość przeprowadzenia badania

3. zbiorowość generalna jest zbiorowością o nieskończonej liczbie elementów (np. eksperymenty w badaniach zjawisk przyrodniczych, badania leków).

Badając część zbiorowości generalnej (tzn. pobierając z niej próbkę) staramy się, aby była ona reprezentatywna, tzn. aby z przyjętą dokładnością opisywała strukturę zbiorowości generalnej. Reprezentatywność próby zależy od sposobu jej wyboru i od jej liczebności. Można wyróżnić 2 sposoby wybierania próby: losowy i nielosowy. Wybór elementu ze zbioru jest losowy, gdy każdy element zbioru ma jednakową szansę znalezienia się w próbie. Wyniki uzyskane z badań takiej próby można uogólniać na zbiorowość generalną. Natomiast wybór celowy polega na tym, że o tym czy dany element znajdzie się w próbie decyduje badacz. W tym przypadku wyniki badania tej próby nie mogą być uogólnione na całą zbiorowość.

Badanie, które obejmuje tylko część zbiorowości nazywamy badaniem częściowym. Występują najczęściej 3 rodzaje badań częściowych:

1. reprezentacyjne - badanie częściowe o losowym doborze jednostek zbiorowości do próby (najlepsze badanie o charakterze częściowym - elementy statystyki matematycznej), np. przy liczeniu indeksu cen dóbr i usług konsumpcyjnych

2. monograficzne - szczegółowa i wszechstronna analiza wybranej części zbiorowości (nie jest oparte na próbie losowej, nie można uogólniać wyników)

3. ankietowe.

Wyróżnić można 4 etapy badania statystycznego:

1. prognozowanie - planowanie badania statystycznego

2. obserwacja statystyczna - zbieranie danych liczbowych

3. opracowanie zebranego materiału statystycznego

4. analiza statystyczna - opis i wnioskowanie statystyczne

Planując badanie należy określić zbiorowość badaną, sposób zbierania danych oraz dokonać wyboru tzw. cech statystycznych, które będą obserwowane. Cechami statystycznymi nazywamy właściwości, którymi odznaczają się jednostki wchodzące w skład badanej zbiorowości np. miejsce zamieszkania, wiek, wysokość pensji, wielkość produkcji przemysłowej pewnego zakładu.

Cechy statystyczne można podzielić na:

• ilościowe (mierzalne) - to takie cechy, których poszczególne warianty dają się wyrazić za pomocą jednostek miary (za pomocą liczb), np. wiek człowieka, liczba dzieci w rodzinie, wzrost,

• jakościowe (niemierzalne) - można podzielić na ciągłe i skokowe. Cechę nazwiemy ciągłą, jeżeli może przyjąć każdą wartość z określonego skończonego przedziału liczbowego, np. wzrost człowieka, wysokość płacy. Przez cechę skokową rozumiemy taką cechę, która może przyjmować tylko niektóre wartości z pewnego przedziału liczbowego, np. liczba osób w rodzinie (liczb całkowite).

Zebrany materiał statystyczny po dokładnej kontroli oddajemy grupowaniu. W rezultacie otrzymujemy tzw. szeregi statystyczne.

Szereg statystyczny - rząd wielkości statystycznych uporządkowanych wg określonego kryterium. Stanowi on podstawowe narzędzie analizy statystycznej. Wyróżnić można następujące rodzaje szeregów statystycznych:

• geograficzne (terytorialne), które przedstawiają rozmieszczenie wielkości statystycznych w przestrzeni

• czasowe (dynamiczne) podające wielkości zjawiska w kolejnych jednostkach czasu

• strukturalne, które przedstawiają strukturę badanej zbiorowości - szeregi te mogą być z cechą mierzalną jak i niemierzalną

• rozdzielcze, które złożone są z dwóch kolumn, przy czym w pierwszej kolumnie wymienione są warianty cechy, a w drugiej - liczba jednostek o danym wariancie.

Bardziej złożoną formą prezentacji tabelarycznej zebranego materiału stanowią tablice statystyczne. Są one zbiorem pewnej liczby szeregów statystycznych i prezentują badaną zbiorowość z punktu widzenia dwóch cech jednocześnie. Każda tablica składa się z następujących elementów:

• numeru porządkowego

• tytułu

• tablicy właściwej

• źródła informacji przedstawionych w tablicy.

Statystyka - wykład 2

(25 lutego'09)

	Główka tablicy
Boczek tablicy

Nie można w tablicy zostawić pustego miejsca!

Znaki umowne stosowane w tablicach statystycznych:

„-” zjawisko nie występuje

„⋅” brak informacji lub brak wiarygodnych informacji

„0” zjawisko występuje, ale w ilości mniejszej niż 0,5 jednostki

„×” rubryka nie może być wypełniona ze względu na układ tablicy

„!” przy liczbach, które zostały w wydawnictwie zmienione w porównaniu z poprzednimi opublikowanymi w wydawnictwach GUS

Liczba osób w rodzinie	Liczba osób pracujących
		0	1	2	3	4
1	15	18	×	×	×
2	23	45	45	×	×
3	43	65	21	23	×

Wskaźnikiem struktury nazywamy iloraz liczebności wyróżnionej części zbiorowości i liczebności całej zbiorowości.

, i=1, 2, 3, …

w procentach:

Wskaźnik natężenia (szczególnie, gdy występuje dużo cech niemierzalnych) - iloraz liczebności dwóch zbiorowości w pewien logiczny sposób ze sobą powiązanych, np. stopa bezrobocia, gęstość zaludnienia.

MIARY PRZECIĘTNE (MIARY TENDENCJI CENTRALNEJ)

Porównanie wskaźników struktury obliczonych dla tych samych grup klasyfikacyjnych w kilku zbiorowościach daje jedynie odpowiedź na pytanie, w której zbiorowości dana grupa jest stosunkowo liczniejsza. Konieczne jest więc obliczanie parametrów, które charakteryzowałyby zbiorowość w taki sposób, że porównanie różnych zbiorowości statystycznych można by sprowadzić do porównania niewielu charakteryzujących je wielkości. Liczby takie nazywane są charakterystykami opisowymi zbiorowości. Miary przeciętne charakteryzują zbiorowość statystyczną niezależnie od różnic pomiędzy obserwacjami. Można je podzielić na dwie zasadnicze grupy:

• klasyczne

• pozycyjne.

Do miar przeciętnych klasycznych zaliczamy średnią arytmetyczną, harmoniczną, geometryczną, kwadratową. W skład grupy miar przeciętnych pozycyjnych wchodzą: mediana, kwartale, dominanta.

Miary przeciętne klasyczne

Średnia arytmetyczna definiowana jest jako iloraz sumy wszystkich wartości cechy i liczebności badanej zbiorowości.

cechy statystyczne: X, Y, Z, …

warianty cech: x₁, x₂, x₃, …

liczba jednostek w przedziałach klasowych: n₁, n₂, n₃, …

dla szeregu szczegółowego

dla szeregu rozdzielczego o klasach jedno-jednostkowych

dla szeregu rozdzielczego o przedziałach klasowych

Ważniejsze własności średniej arytmetycznej:

1. suma wartości cechy X jest równa średniej arytmetycznej pomnożonej przez liczebność zbiorowości, czyli
.

2. suma odchyleń poszczególnych wartości cechy od średniej arytmetycznej jest równa 0, czyli
.

3. średnia arytmetyczna jest wielkością mianowaną - jest wyrażona w takich samych jednostkach jak badana cena.

4. obliczanie średniej arytmetycznej oparte jest na wszystkich obserwacjach.

5. średnia arytmetyczna obliczona na podstawie szeregu rozdzielczego o przedziałach klasowych jest wartością przybliżoną, przy czym wielkość tego przybliżenia zależy od zastosowanej metody grupowania danych statystycznych. (Im mniejsze przedziały, tym mniejszy błąd).

6. w przypadku szeregu rozdzielczego obliczenie średniej arytmetycznej możliwe jest tylko wtedy, gdy jest to szereg o domkniętych przedziałach klasowych.

7. nie jest wskazane obliczanie średniej arytmetycznej, gdy w niezbyt licznej zbiorowości występują wielkości skrajne (nietypowe).

8. nie należy obliczać średniej arytmetycznej w przypadku, gdy badana zbiorowość jest z punktu widzenia danej cechy niejednorodna.

Średnia harmoniczna - należy ją stosować w przypadku, gdy wartości cechy podane w formie odwrotności, tzn. gdy wartości tej cechy przedstawione są w postaci liczb względnych. Stosowana powinna być przede wszystkim wtedy, gdy występują duże różnice pomiędzy obserwacjami, ponieważ jest mniej wrażliwa na wartości nietypowe niż średnia arytmetyczna.

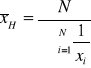
Średnia geometryczna - trafniej niż średnia arytmetyczna charakteryzuje cechę, gdy wartości tej cechy przedstawione są w postaci liczb względnych. Stosowana powinna być przede wszystkim wtedy, gdy występują duże różnice pomiędzy obserwacjami, ponieważ jest mniej wrażliwa na wartości nietypowe niż średnia arytmetyczna.

Miary przeciętne pozycyjne - wartości cechy pewnych jednostek zbiorowości uwzględnionych ze względu na jej położone w tej zbiorowości. Przy wyznaczaniu tych miar wartości cechy muszą być uporządkowane niemalejąco lub nierosnąco.

Mediana (drugi kwartyl, wartość środkowa) - wartość cechy mierzalnej w uporządkowanym ich zbiorze, poniżej i powyżej której znajduje się jednakowa liczba jednostek zbiorowości statystycznej.

Metody obliczeń mediany:

1. gdy podstawą obliczeń jest szereg szczegółowy

, gdy N jest nieparzyste

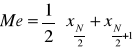
, gdy N jest parzyste

2. gdy podstawą obliczeń jest szereg rozdzielczy

,

gdzie
, gdy N jest parzyste i
, gdy N jest nieparzyste

Mediana jest wartością mianowaną. Jej wartość nie zależy od nietypowych wartości cechy. Wyznaczona może być w przypadku, gdy szereg klasowy ma otwarte przedziały, należy jednak pamiętać, że mediana obliczona na podstawie szeregu rozdzielczego jest wielkością przybliżoną.

Statystyka - wykład 3

(4 marca'09)

Dominanta (moda) - to wartość cechy jednostki statystycznej, która w badanej zbiorowości występuje najczęściej (najliczniej). Istnieje możliwość wyznaczenia przybliżonej wartości dominanty z szeregu rozdzielczego, jednak muszą być spełnione 2 warunki:

w szeregu musi występować przedział klasowy o największej liczebności

rozpiętość tego przedziału oraz rozpiętości przedziałów bezpośrednio z nim sąsiadujących muszą być identyczne. Wówczas przybliżoną wartość dominanty oblicza się ze wzoru

.

MIARY ZRÓŻNICOWANIA (ROZPROSZENIA, ROZRZUTU, DYSPERSJI)

Miary przeciętne nie dają wyczerpującej charakterystyki szeregu statystycznego, nie charakteryzują jego budowy i nie pozwalają przeniknąć w wewnętrzny układ zbiorowości. Zadaniem miar zróżnicowania jest wskazanie, w jakim stopniu poszczególne wartości cechy jednostek zbiorowości statystycznej koncentrują się wokół wartości przeciętnej badanej cechy. Stopień, w jakim poszczególne wartości cechy odbiegają od wartości przeciętnej, czyli stopień zróżnicowania decyduje niejednokrotnie o znaczeniu danej średniej jako charakterystyki badanego szeregu. Im mniejszy stopień zróżnicowania, tym większe znaczenie danej średniej. Miary zróżnicowania podzielić można na miary klasyczne i pozycyjne.

Do klasycznych miar zróżnicowania zaliczamy: odchylenie przeciętne, wariancja i odchylenie standardowe.

Do pozycyjnych miar zróżnicowania zaliczamy: obszar zmienności (rozstęp) i odchylenie ćwiartkowe.

Klasyczne miary zróżnicowania

Odchylenie przeciętne - w przypadku danych szczegółowych odchylenie przeciętne wyrażone jest wzorem:

.

Natomiast gdy podstawę obliczeń stanowi szereg rozdzielczy o domkniętych przedziałach klasowych:

.

Jest wielkością mianowaną. Jego interpretacja powinna być przeprowadzona w odniesieniu do średniej: im większą część średniej stanowi obliczone odchylenie przeciętne, tym większe jest zróżnicowanie wartości badanej cechy.

Wariancja - w przypadku danych szczegółowych wyrażona jest wzorem:

,

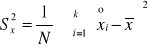
do obliczeń:
.

W przypadku, gdy podstawę obliczeń stanowi szereg rozdzielczy, wyrażona jest wzorem:
,

do obliczeń:
.

Odchylenie standardowe - definiowane jest jako pierwiastek kwadratowy z wariancji. W przypadku danych szczegółowych wyrażone jest wzorem

,

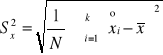
do obliczeń:
.

W przypadku szeregu rozdzielczego wzór ma postać:

,

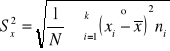
do obliczeń:
.

Miara ta jest wielkością mianowaną, przy tym zróżnicowanie wartości cechy jest duże, gdy odchylenie standardowe stanowi znaczną część średniej arytmetycznej.

Pozycyjne miary zróżnicowania

Obszar zmienności - definiowany jako różnica między największą najmniejszą wartością cechy:
. Miara ta posiada niezbyt duże znaczenie praktyczne, ponieważ reaguje na nietypowe wartości cechy. Wykorzystywana jest podczas kontroli jakości i wstępnych analizach statystycznych.

Odchylenie ćwiartkowe definiowane jest jako połowa różnicy trzeciego i pierwszego kwartyla:

.

Jeżeli Q_x stanowi znaczną część mediany wówczas oznacza to silne zróżnicowanie wartości danej cechy.

Względne miary zróżnicowania (współczynniki zmienności)

1. współczynnik zmienności oparty na odchyleniu przeciętnym:

.

Informuje on, jaki procent średniej arytmetycznej stanowi odchylenie przeciętne.

2. współczynnik zmienności oparty na odchyleniu standardowym:

.

Informuje on, jaki procent średniej arytmetycznej stanowi odchylenie standardowe.

3. współczynnik zmienności oparty na odchyleniu ćwiartkowym:

.

Informuje on, jaki procent mediany stanowi odchylenie ćwiartkowe.

Im większa wartość danego współczynniki tym większe jest zróżnicowanie wartości cechy.

Miary asymetrii (skośności)

Często interesuje nas fakt czy odchylenia od wartości przeciętnej w jedną stronę są mniej lub więcej liczne od odchyleń w drugą stronę. Zagadnienie to można zbadać za pomocą miar asymetrii.

Kształt idealny krzywej liczebności (symetryczny) - rozkład badanej zbiorowości jest rozkładem symetrycznym; szereg, który był podstawą wykresu jest szeregiem symetrycznym.

W takiej sytuacji zachodzi zależność
. (!Ale nie musi zachodzić odwrotnie: Gdy miary są równe to szereg nie musi być symetryczny!)

Częściej krzywa jest zdeformowana:

asymetria lewostronna (ujemna)

asymetria prawostronna (dodatnia)

Różnica między średnią arytmetyczną a dominantą:

Jeżeli
to jest asymetria ujemna (lewostronna)

Jeżeli
to jest asymetria dodatnia (prawostronna)

Miara ta nie nadaje się do porównań.

Współczynnik asymetrii

Jego znak informuje o kierunku asymetrii:

Jeżeli
to jest asymetria ujemna (lewostronna)

Jeżeli
to jest asymetria dodatnia (prawostronna)

Im wartość bezwzględna W_s jest bliższa zeru, tym asymetria rozkładu cechy jest mniejsza.

Współczynnik asymetrii oparty na momentach

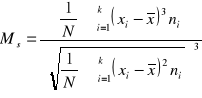
Jego własności są analogiczne do poprzedniego współczynnika.

Współczynnik asymetrii oparty na kwartylach (gdy nie można obliczyć średniej arytmetycznej)

.

Znak As informuje o kierunku asymetrii, a wartość bezwzględna tej miary informuje o sile asymetrii.

Jeżeli rozkład badanej cechy charakteryzuje się niewielką asymetrią, to ma miejsce przybliżony wzór:

.

Statystyka - wykład 4

(11 marca'09)

Analiza regresji i korelacji

Zależność korelacyjna - jeżeli zmianom wartości jednej cechy odpowiadają zmiany średnich wartości drugiej cechy, to powiemy, że między tymi cechami występuje zależność korelacyjna.

Badana jest zbiorowość z punktu widzenia dwóch cech, między którymi występuje zależność korelacyjna. Możemy potraktować odpowiadające sobie wartości tych cech jako współrzędne punktów, a następnie sporządzić wykres tych punktów na płaszczyźnie. Może zdarzyć się, że wykreślone punkty skupiają się wokół pewnej linii prostej. W takim przypadku powiemy, że między badanymi cechami występuje zależność korelacyjna prostoliniowa. Jeżeli wykreślone punkty koncentrują się wokół pewnej linii krzywej, to powiemy, że między badanymi cechami występuje zależność korelacyjna krzywoliniowa. Jeżeli w miarę wzrostu wartości cechy X (cecha niezależna), wzrastają na ogół odpowiadające im wartości cechy Y, to powiemy, że między tymi cechami występuje korelacja dodatnia. Jeżeli w miarę wzrostu X maleją z reguły odpowiadające im wartości cechy Y, to między nimi występuje korelacja ujemna.

Miary ścisłości związku korelacyjnego dwóch cech

Współczynnik korelacji liniowej Pearsona - jego zadaniem jest ocena siły i kierunku zależności korelacyjnej dwóch cech w sytuacji, gdy między nimi jest korelacja prostoliniowa.

Do obliczeń można wykorzystać wzór:

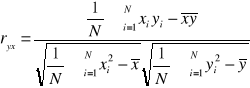
Własności:

1. współczynnik korelacji przyjmuje zawsze wartości z przedziału domkniętego <-1,1>

2. o sile zależności korelacyjnej informuje moduł |r_yx|. Im wartość tego modułu bliższa jedności, tym silniejsza jest zależność między badanymi cechami. Bliskie zeru świadczą o bardzo słabej zależności, bądź o jej braku. W szczególności, gdy moduł |r_yx|=1, to między cechami występuje zależność funkcyjna, którą można opisaćza pomocą równania linii prostej.

3. znak współczynnika korelacji informuje o kierunku zależności (r_yx>0 - korelacja dodatnia, r_yx<0 - korelacja ujemna)

4. miara ta jest symetryczna: r_yx=r_xy.

Stosunek korelacji - wykorzystywany jest do badania siły należności korelacyjnej dwóch cech, z których przynajmniej jedna jest cechą niemierzalną. Podstawą do obliczania tej miary są pogrupowane dane w postaci tzw. tablicy korelacyjnej.

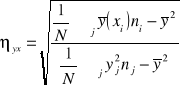
Własności:

1. stosunek korelacji przyjmuje zawsze wartości w przedziału domkniętego <0,1>

2. im bliżej jedności, tym silniejsza zależność między cechami. Wartości bliskie zeru świadczą o słabej zależności lub jej braku. W szczególności η_yx=1 oznacza, że między cechami jest zależność funkcyjna (korelacja funkcyjna)

3. miara ta jest niesymetryczna: η_yx≠η_xy

4. jeżeli moduł |r_yx|=η_yx oznacza to, że między badanymi cechami występuje zależność korelacyjna prostoliniowa.

Do pomiaru siły zależności między dwoma cechami niemierzalnymi wykorzystuje się współczynnik kontyngencji C-Pearsona:

,

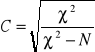
gdzie

.

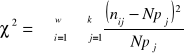
Podstawą obliczeń χ² stanowią dane pogrupowane w postaci tablicy, która nazywana jest tablica niezależności.

Własności:

1. współczynnik kontyngencji C-Pearsona przyjmuje zawsze wartości z przedziału lewostronnie domkniętego <0,1)

2. zależność jest tym silniejsza, im bliższa jedności jest wartość cechy

Jeżeli tablica ma wymiary mniejsze niż 3×3 to liczymy korelacje χ=2×2.

Analiza dygresji

Dygresja prostoliniowa

Badana jest zbiorowość z punktu widzenia dwóch cech, między którymi występuje korelacja prostoliniowa. Wiadomo, że w takim przypadku wykreślone punkty, których współrzędnymi są odpowiadające sobie wartości cech, będą skupiały się wokół pewnej linii prostej. Znajdujemy równanie linii prostej, wokół której punkty wykresu są najbardziej skupione. Linię taką nazywamy linią (funkcją) regresji. Jej równanie zapisujemy wzorem
.

Znalezienie równania tej linii „na oko” nie jest możliwe. W celu jej znalezienia zastosowania jest metoda najmniejszych kwadratów (mnk). W metodzie tej zakłada się, że linia prosta, wokół której punkty wykresu są najbardziej skupione powinna spełniać warunek
.

i
.

Aby powyższa suma kwadratów osiągała minimum możemy potraktować ją jako funkcję dwóch zmiennych i wykorzystać warunek konieczny istnienia ekstremum tej funkcji. Z warunku tego wynika, że pochodne cząstkowe
muszą się równać zeru. W rezultacie otrzymujemy układ dwóch równań o niewiadomych a i b, który nazywany jest układem równań normalnych.

Statystyka - wykład 5

(18 marca'09)

Układ równań normalnych ma postać:

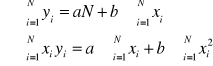
Parametr b z równania linii regresji ma następującą interpretację: informuje o ile wzrośnie lub zmaleje wartość cechy Y, gdy wartość cechy X zwiększy się o jednostkę. Możemy oszacować wartość cechy Y na podstawie tego równania przy określonej wartości cechy X - znajomość równania linii regresji umożliwia sporządzanie prognoz. Jest jednak oczywiste, że każda prognoza obarczona będzie pewnym błędem, którego wielkość możemy ocenić obliczając tzw. odchylenie standardowe resztowe, które wyrażone jest wzorem:

.

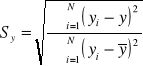
Między cechami występuje współzależność:

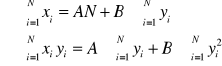
Można obliczyć współczynnik korelacji:

(sgnb - znak b)

Jeżeli b i B są ujemne to
.

Jeżeli b i B SA dodatnie to
.

Można ominąć rozwiązywanie dwóch równań, gdy mamy dane: r_yx, S_y, S_x, ȳ, x.

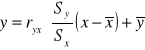
regresja prostoliniowa

regresja krzywoliniowa

dla

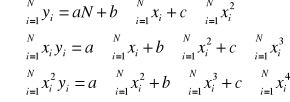
Parametry struktury stochastycznej

Współczynnik zbieżności mierzący jaka część zaobserwowanej zmienności zmiennej y jest dziełem przypadku. Oblicz się go wg wzoru:

.

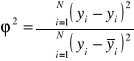
Jeżeli parametry równania linii regresji są szacowane metodą najmniejszych kwadratów, zawsze zachodzi relacja
, przy czym
bliskie zeru oznacza dużą zmienność danych empirycznych z danymi teoretycznymi, a zatem przyjęta postać funkcji regresji dobrze opisuje zależność zachodzącą między cechami X i Y.

Współczynnik determinacji - określa jaka część zmiennej zależnej y jest wyjaśniana przez zmienność wartości zmiennej niezależnej x; wyrażony jest wzorem
. Można wykazać, że
.

Korelacja cząstkowa - polega na porównaniu każdorazowo ze sobą dwóch cech z jednoczesnym założeniem, że istnieją i mają wpływ na dane zjawisko inne cechy, od których świadomie się abstrahuje poprzez ich eliminowanie. Przypuśćmy, że mamy do czynienia z trzema cechami, których związek chcemy zbadać. Oznaczmy je liczbami 1,2,3. Można znaleźć współczynnik korelacji dwóch z tych cech przy wyłączeniu oddziaływania trzeciej. Współczynnik korelacji cząstkowej w przypadku trzech cech zapisujemy w następujący sposób: r12.3, r13.2, r23.1, gdzie pierwsze dwie cyfry jako subskrypty przed kropką oznaczają cechy, między którymi poszukujemy korelacji, natomiast subskrypty po kropce oznaczają cechy wywierające wpływ na korelację dwóch pozostałych cech, które chcemy w danym przypadku wyeliminować. Wzory na współczynniki korelacji cząstkowej mają postać:

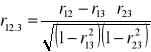
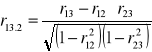
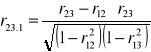
Analiza dynamiki zjawisk

Podstawy analizy dynamiki zjawisk stanowią tzw. szeregi czasowe (dynamiczne), które prezentują zmiany zjawiska w czasie. Wyróżnić można 2 rodzaje szeregów czasowych, a mianowicie szeregi okresów i szeregi momentów. Szeregi okresów przedstawiają wielkość zjawiska w poszczególnych okresach czasu, natomiast szeregi momentów prezentują wielkość zjawiska w ściśle określonym momencie czasu.

Statystyka - wykład 6

(25 marca'09)

W przypadku szeregów okresów możliwa jest ocena przeciętnego poziomu zjawiska oraz stopnia jego zróżnicowania w okresie objętym analizą. W tym celu wykorzystywana może być średnia arytmetyczna i odchylenie standardowe (współczynnik zmienności). W przypadku szeregu momentów możliwa jest jedynie przybliżona ocena przeciętnego poziomu zjawiska w okresie objętym analizą. Wykorzystywana jest tu średnia chronologiczna, która wyrażona jest wzorem:

.

(miara mocno przybliżona)

Indywidualne wskaźniki dynamiki (indeksy indywidualne)

Do oceny wielkości zmian zjawiska w dwóch okresach stosuje się indeksy indywidualne. Wyróżnić można 2 rodzaje indeksów indywidualnych, a mianowicie indeksy jednopodstawowe i łańcuchowe.

Indeksy jednopodstawowe - informują o zmianach w wielkościach zjawiska w poszczególnych okresach w porównaniu z wielkością zjawiska z okresu, który wybrany został jako podstawa porównań. Wybór podstawy porównań zależy od celu badania. Nie powinien to być jednak okres, w którym wielkość zjawiska jest nietypowa (nadmiernie wysoka/niska). Indeksy jednopodstawowe obliczane są wg wzoru:

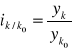
, k=1,2,3,…

w procentach:

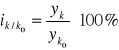
Indeksy łańcuchowe - informują o zmianach wielkości zjawiska w poszczególnych okresach w porównaniu z okresami wcześniejszymi:

w procentach:

.

Do oceny przeciętnego okresowego tempa zmian zjawiska w okresie objętym analizą wykorzystywana jest średnia geometryczna z indeksów łańcuchów, które obliczone są dla analizowanego okresu:

gdzie

.

Wzór ten można przekształcić do prostszej postaci:

.

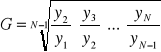
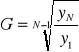
Do interpretacji wykorzystuje się wyrażenie w postaci
.

Agregatowe indeksy (zespołowe) dla wielkości absolutnych

Stosowane są w przypadku, gdy zjawisko, którego zmiany w czasie chcemy określić, ma charakter agregatu, którego poszczególne składniki nie są bezpośrednio sumowane.

p₀, p₁ - ceny towaru odpowiednio w czasie podstawowym i badanym

Indywidualny indeks cen:

q₀, q₁ - ilość towaru odpowiednio w okresie podstawowym i badanym

Indywidualny indeks ilości:
.

Agregatowy indeks wartości: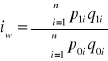
.

Obliczanie wyłącznie indeksu wartości jest niewystarczające. Nie jesteśmy w stanie określić w wyniku czego nastąpił wzrost lub spadek wartości produkcji. Zachodzi zatem konieczność obliczenia dodatkowych indeksów, które pozwoliłyby odpowiedzieć na postawione pytanie. Funkcje takie pełnią agregatowe indeksy ilości i cen.

Agregatowe indeksy ilości - konstruowane są przy założeniu, że w porównywanych okresach ceny towarów nie zmieniały się. jeżeli przyjmiemy, że w porównywanych okresach ceny towarów nie zmieniały się i były takie jak w okresie podstawowym wówczas otrzymamy agregatowy indeks ilości Laspeyresa:

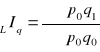
Gdy przyjmiemy założenie, że w porównywanych okresach ceny towarów nie zmieniały się i były takie jak w okresie badanym, wówczas otrzymamy agregatowy indeks ilości Paaschego:

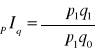
Agregatowe indeksy cen - konstruowane są przy założeniu, że w porównywanych okresach ilości produkowanych towarów nie zmieniły się. Gdy przyjmiemy, że w porównywanych okresach ilości towarów nie zmieniały się, były takie same jak w okresie podstawowym, wówczas otrzymamy agregatowy indeks cen Laspeyresa:

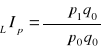
Jeżeli przyjąć, że w porównywanych okresach ilości towarów nie zmieniały się i były takie jak w okresie badanym, wówczas otrzymamy agregatowy indeks cen Paaschego:

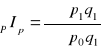
Zachodzą następujące relacje, zwane równościami indeksowymi, a mianowicie:

Statystyka - wykład 7

(1 kwietnia'09)

Metody wyodrębniania głównej tendencji rozwojowej zjawisk (trend)

Wyróżniamy 2 metody: mechaniczną i analityczną. Metoda mechaniczna polega na obliczaniu tzw. średnich ruchomych. W praktyce najczęściej obliczane są średnie ruchome o nieparzystej liczbie okresów, tzn. trzyokresowe, pięciookresowe, itd. Przykładowo obliczanie średnich ruchomych trzyokresowych odbywa się w następujący sposób: podstawę obliczeń średnich stanowi szereg czasowy, bierzemy pod uwagę 3 pierwsze obserwacje i obliczamy z nich
, pomijamy obserwację pierwszą, dołączamy czwartą i z tych obserwacji obliczamy
.

Procedurę tę kontynuujemy aż do wyczerpania wszystkich obserwacji w szeregu czasowym. Wykreślony szereg złożony ze średnich ruchomych pozwala lepiej zaobserwować tendencję rozwojową badanego zjawiska. Metoda analityczna: sporządzając wykres szeregu czasowego często można zaobserwować, że punkty tego wykresu skupiają się wokół pewnej linii prostej. Stawiamy sobie zadanie odnalezienia równania tej linii prostej, wokół której punkty wykresu są najbardziej skupione. Taką linię nazywa się linią (funkcją) trendu. Jej równanie można zapisać ogólnie wzorem
, gdzie t jest zmienną niezależną określającą czas. Znalezienie równania linii trendu „na oko” jest niemożliwe. Stąd też, podobnie jak w przypadku linii regresji dla znalezienia równania linii trendu wykorzystuję się metodę najmniejszych kwadratów. W rezultacie otrzymujemy układ dwóch równań o niewiadomych a i b, który nazywany jest układem równań normalnych:

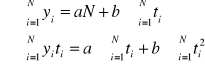
Parametr b ma następującą interpretację ekonomiczną - informuje on jak średnio zmienia się wielkość zjawiska z okresu na okres.

Znajomość równania linii trendu umożliwia sporządzanie prognoz, tzn. można szacować wielkość zjawiska w przyszłości. Jest jednak oczywiste, że każda prognoza obarczona jest pewnym błędem. Jego wielkość można oszacować obliczając odchylenie standardowe resztowe:

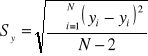
Wyodrębnianie wpływu równań sezonowych

Wpływ wahań sezonowych można wyznaczyć za pomocą metody analitycznej i mechanicznej. Metoda analityczna polega na wyznaczaniu tzw. wskaźników sezonowości:

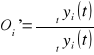
Jeżeli suma
, gdzie d jest liczbą podokresów wyróżnionych w roku, to obliczamy skorygowane wskaźniki sezonowości:

, gdzie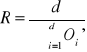
.

Wpływ czynnika sezonowego w wielkościach bezwzględnych można wyznaczyć ze wzoru:

, i=1,…,d

---