Akademia Górniczo - Hutnicza.

Wydział Wiertnictwa Nafty i Gazu.

Specjalność: Ochrona Środowiska.

Laboratorium z Geofizyki Poszukiwawczej

i Wiertniczej.

Ćw.nr.7: Badanie własności sprężystych skał.

Dariusz Sobala

Paweł Sołtys

Rok III

1. Cel ćwiczenia.

Celem ćwiczenia jest określenie własności sprężystych skał.

2. Wstęp teoretyczny.

Badania własności sprężystych próbek skał znalazły szerokie zastosowanie w geofizyce, zarówno przy rozwiązywaniu szeregu zagadnień geologiczno-złożowych, jak i dla interpretacji pomiarów sejsmicznych.

Prowadzone badania laboratoryjne umożliwiają określenie prędkości rozchodzenia się fal podłużnych i poprzecznych, wielkości współczynnika tłumienia oraz takich parametrów sprężystości, jak modułu sprężystości podłużnej (Younga) i stałej Poissona.

Dla ośrodka nieorganicznego, izotropowego i sprężystego związki między prędkością rozchodzenia się fal a parametrami sprężystości są następujące:

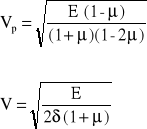
gdzie: V_p - prędkość fali podłużnej,

V_s - prędkość fali poprzecznej,

E - moduł sprężystości podłużnej (Younga),

- gęstość ośrodka,

- moduł skurczenia poprzecznego (stała Poissona).

Ze wzorów wynika, że prędkości fal podłużnych i poprzecznych są związane zależnością:

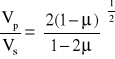
Stała Poissona
może się zmieniać w granicach od 0 - 0,5 , dlatego też prędkość fal podłużnych jest zawsze większa od fal poprzecznych. Przyjmując najczęściej występującą wartość
dla skał równą 0,25 , stosunek:

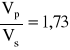
Prędkość rozchodzenia się fal sprężystych w skałach zależy od ich składu mineralnego, a ponadto od takich czynników, jak: porowatość, wilgotność i głębokość występowania.

W skałach zwięzłych prędkość rozchodzenia się fal sprężystych zależy głównie od gęstości szkieletu. W zakresie zmian porowatości od 5 do 30% zależność ta jest bliska liniowej i może być określona z tzw. Równania średniego czasu:

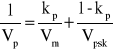
gdzie: V_p, V_m, V_psk - prędkości rozchodzenia się podłużnej fali sprężystej odpowiednio w skale, w medium nasycającym skałę oraz w szkielecie skały.

W skałach porowatych prędkość fal sprężystych jest określona głównie wielkością porowatości oraz własności medium nasycającego pory. Wpływ medium nasycającego jest uwarunkowany takimi jego parametrami, jak: gęstość, ściśliwość i lepkość.

Wpływ współczynnika porowatości na prędkość fal podłużnych nie jest określony jednoznacznie zależnością. Dla określenia prędkości fali podłużnej w skale porowatej jest konieczna znajomość fali w jej szkielecie.

Prędkości fal sprężystych w ośrodku uwarstwionym zależą od kierunku w jakim się je mierzy. Prędkości mierzone w kierunku równoległym do uwarstwienia V_prów są zawsze większe od prędkości w kierunku prostopadłym do uwarstwienia V_ppro. Dla oceny różnic w prędkościach fal posługujemy się współczynnikiem anizotropii prędkości:

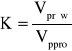
gdzie: V_prów - prędkość rozchodzenia się podłużnej w kierunku równoległym do uwarstwienia,

V_ppro - prędkość rozchodzenia się fali podłużnej w kierunku prostopadłym do uwarstwienia.

Fale sprężyste rozchodzą się w skałach (ośrodku niejednorodnym i nieidealnie sprężystym) ulegają zjawisku pochłaniania i rozpraszania. Zjawiska te wywołane są wieloma czynnikami i zależą głównie od budowy i własności skał, mediów je nasycających oraz częstotliwości drgań sprężystych.

Prowadząc pomiary na rdzeniach wiertniczych należy pamiętać, że mamy do czynienia nie z ośrodkiem nieorganicznym (masywem), lecz z cylindrem o małej średnicy. Stąd prędkość mierzona w danym rdzeniu może nie być prędkością rozchodzenia się fali w masywie V_M , lecz w pręcie V_PR.

3. Otrzymane wyniki i ich interpretacja.

Tabela wyników:

Symbol próbki	Kierunek badania	Droga [mm]	Czas podłużna [ 10^-6s]	Czas poprzeczna [ 10^-6s]	Prędkość podłużna [m/s]	Prędkość poprzeczna [m/s]
szkło organiczne	szkło organiczne	140.00	51,4	100,8	2776	1403
powietrze	powietrze	25	74	-	342	-
powietrze	powietrze	35	102,9	-	343	-
powietrze	powietrze	50	150,4	-	335	-
116D	równoległy	38,2	8,5	16,2	5093	2513
116D	prostopadły	42,5	11,2	18,9	4167	2374
2A	równoległy	63,9	12,8	20,5	5415	3277
2A	prostopadły	65,8	13,5	20,2	5264	3427

Poszukiwaną prędkość fali sprężystej możemy obliczyć z zależności:

gdzie: l - długość badanej próbki w metrach

t - czas przebiegu impulsu w sekundach

t_o - poprawka na czas opóźnienia w aparaturze i czujnikach, wyznaczona przy zetknięciu czujników w sekundach.

Czas opóźnienia aparatury t_o=1,0*10^-6 [s].

Dokładności odczytu czasu i długości przyjmujemy:

Δt = 0,1 [μs],

Δl = 0,05 [mm].

Obliczenie błędu bezwzględnego i względnego prędkości dla jednej z próbek (P2) metodą różniczki zupełnej:

• dla fali podłużnej

- w kierunku równoległym 116D

• w kierunku prostopadłym116D

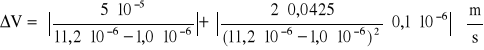
• dla fali poprzecznej

- w kierunku równoległym2A

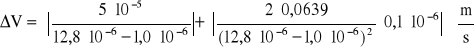
• w kierunku prostopadłym

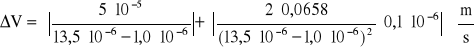
Obliczenie błędów względnych

• dla fali podłużnej

• w kierunku równoległym

• w kierunku prostopadłym

• dla fali poprzecznej

• w kierunku równoległym

• w kierunku prostopadłym

Obliczenie współczynnika anizotropii dla próbek 2A i 116A:

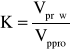
gdzie:

V_prów - prędkość rozchodzenia się fali podłużnej w kierunku równoległym

V_ppro - prędkość rozchodzenia się fali podłużnej w kierunku prostopadłym

• dla próbki 2A

• dla próbki 116A

Obliczanie wartości modułu Younga E, sztywności G i stałej Poissona μ .

Dla każdej próbki przyjmujemy gęstość skały δ=2,6 [g/cm³] =2600 [kg/m³]

• obliczenia dla próbki 2A:

Moduł sprężystości podłużnej Younga E:

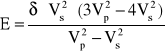
gdzie:

V_s - prędkość poprzeczna,

V_p - prędkość podłużna.

• w kierunku równoległym

E = 28,13*10⁹ 5,74*10¹⁰[Pa]

• w kierunku prostopadłym

E = 50,23*10⁹ 1,21*10¹⁰[Pa]

Moduł skurczenia poprzecznego. Stała Poissona μ:

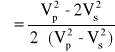
• w kierunku równoległym

μ = 0,44

• w kierunku prostopadłym

μ = 0,45

Moduł sprężystości postaci. Moduł sztywności G:

• w kierunku równoległym

G = 2,01*10⁹ [Pa]

• w kierunku prostopadłym

G = 4,24*10⁹ [Pa]

• obliczenia dla próbki 116A

Moduł sprężystości podłużnej Younga E:

• w kierunku równoległym

E = 4,95*10⁹ [Pa]

• w kierunku prostopadłym

E = 10,3*10⁹ [Pa]

Moduł skurczenia poprzecznego. Stała Poissona μ:

• w kierunku równoległym

μ = 0,46

• w kierunku prostopadłym

μ = 0,43

Moduł sprężystości postaci. Moduł sztywności G:

• w kierunku równoległym

G = 1,5*10⁹ [Pa]

• w kierunku prostopadłym

G = 3,1*10⁹ [Pa]

4. Wnioski.

Na podstawie otrzymanych wartości prędkości rozchodzenia się podłużnej fali sprężystej i porównania ich z wartościami tabelarycznymi stwierdziliśmy, że badane próbki 2A i 116A są piaskowcami zwięzłymi. Po obliczeniu prędkości dla równoległego i prostopadłego kierunku badania, zauważyliśmy, że dla próbki 2A nie ma znacznych różnic wartości prędkości rozchodzenia się fal w przeciwieństwie do wyników dla próbki 116A. Potwierdziły to późniejsze obliczenia współczynnika anizotropii. Różnice wartości modułu Younga, stałej Poissona i modułu sztywności dla poszczególnych próbek mogą wynikać z:

• trudność w ustaleniu granicy fal podłużnych i poprzecznych,

- kierunkowego ułożenia kryształów w skale,

• wpływu otoczenia na wyniki,

• niedokładnego działania przyrządu ze względu na walcową budowę próbek (pomiar w kierunku prostopadłym)

---