Metrologia - laboratorium
Imię i nazwisko: Katarzyna Peta, Arkadiusz Pietrowiak, Wojciech Sarnecki	Semestr: III	Wydział: BM i Z	Kierunek: ZiIP	Grupa: ZP4
Temat ćwiczenia: Statystyczne opracowanie pomiarów.
Data oddania sprawozdania: 25.01.2010		Ocena:

1.Pomiar jest doświadczalnym procesem poznawczym, którego celem jest porównanie mierzonej wielkości a₁ wielkości A z wybraną jednostką miary a₀ tej wielkości w celu wyznaczenia ich stosunku liczbowego n_i= - a₁/a₀ . Wartości te dokonane są w określonych warunkach przy pomocy specjalnych środków pomiarowych. W wyniku pomiaru otrzymana wielkość x wielkości mierzonej jest większa od a i mniejsza od a; przy czym a≠b.

b-a = 2ε>0

Stwierdzenie to jest postulatem metrologii, zgodnie z którym wynik pomiaru jest zawsze obarczony błędem:

y= x +δx

y- wynik pomiaru

x-wartość wielkości mierzonej

δx- błąd pomiaru wartości wielkości mierzonej

Klasyfikacja błędów:

-błędy systematyczne δ_s

-błędy przypadkowe δ_p

Błąd pomiaru: δ_x=δ_s+δ_p

2.Wyniki:

Odchyłka [µm]	Odchyłka [µm]	Odchyłka [µm]	Odchyłka [µm]	Odchyłka [µm]
-10,5	-3,6	-0,8	1,8	4,2
-10	-3,6	-0,6	1,8	4,5
-10	-3,6	-0,6	1,8	4,5
-9,5	-3,4	-0,6	2	4,5
-9	-3,4	-0,4	2	4,5
-8	-3,2	-0,4	2	4,5
-8	-3,2	-0,4	2	4,6
-8	-3	-0,2	2	4,8
-8	-3	-0,2	2	5
-7,5	-2,6	0	2,2	5
-7	-2,6	0	2,2	5
-6,5	-2,4	0	2,4	5
-6,5	-2,2	0	2,4	5
-6,5	-2,2	0	2,4	5
-6	-2	0,2	2,5	5
-5,5	-2	0,2	2,6	5
-5,5	-2	0,2	2,6	5
-5,5	-1,8	0,2	2,8	5,5
-5,5	-1,8	0,4	2,8	5,5
-5,5	-1,8	0,4	2,8	5,5
-5	-1,8	0,4	3	5,5
-5	-1,8	0,6	3	6
-5	-1,8	0,8	3	6
-5	-1,6	1	3,2	6,5
-4,8	-1,6	1	3,2	6,5
-4,8	-1,6	1	3,4	6,5
-4,6	-1,6	1	3,4	6,5
-4,5	-1,4	1	3,4	7
-4,5	-1,4	1	3,4	7
-4,4	-1,2	1,2	3,6	8
-4,4	-1,2	1,4	3,6	8,5
-4,4	-1,2	1,5	3,6	9
-4,4	-1	1,6	3,6	9
-4,2	-1	1,6	3,6	10
-4,2	-1	1,6	3,8	11
-4	-1	1,6	4	11
-4	-1	1,6	4	12
-4	-0,8	1,6	4	13
-3,8	-0,8	1,8	4,2	13,5
-3,6	-0,8	1,8	4,2

3.Obliczanie wartości średniej, wariancji i odchylenia standardowego

Lp.	Przedział (μm)	Liczność ni	środek przedziału xi	Częstotliwość względna m(n)	Częstotliwość skumulowanaΣm(n)	xi n	(xi-xśr)^2 ni	(xi-xśr)^2
1	(-10,5;-9,5)	4	-9	0,020	0,020	-36	351,704	87,926
2	(-9,5;-8,5)	5	-8	0,025	0,045	-40	350,861	70,172
3	(-8,5;-7,5)	5	-7	0,025	0,070	-35	272,092	54,418
4	(-7,5;-6,5)	6	-6	0,030	0,101	-36	243,988	40,665
5	(-6,5;-5,5)	9	-5	0,045	0,146	-45	260,198	28,911
6	(-5,5;-4,5)	14	-4	0,070	0,216	-56	268,200	19,157
7	(-4,5;-3,5)	8	-3	0,040	0,256	-24	91,227	11,403
8	(-3,5;-2,5)	16	-2	0,080	0,337	-32	90,393	5,650
9	(-2,5;-1,5)	17	-1	0,085	0,422	-17	32,229	1,896
10	(-1,5;0,5)	17	0	0,085	0,508	0	2,415	0,142
11	(0,5; 1,5)	11	1	0,055	0,563	11	4,271	0,388
12	(1,5; 2,5)	23	2	0,116	0,678	46	60,594	2,635
13	(2,5; 3,5)	14	3	0,070	0,749	42	96,330	6,881
14	(3,5; 4,5)	17	4	0,085	0,834	68	223,159	13,127
15	(4,5; 5,5)	15	5	0,075	0,910	75	320,598	21,373
16	(5,5;6,5)	6	6	0,030	0,940	36	189,717	31,619
17	(6,5;7,5)	2	7	0,010	0,950	14	87,7313	43,866
18	(7,5;8,5)	2	8	0,010	0,960	16	116,224	58,112
19	(8,5;9,5)	2	9	0,010	0,970	18	148,717	74,358
20	(9,5;10,5)	1	10	0,005	0,975	10	92,605	92,604
21	(10,5;11,5)	2	11	0,010	0,985	22	225,701	112,851
22	(11,5;12,5)	1	12	0,005	0,990	12	135,097	135,097
23	(12,5;13,5)	2	13	0,010	1	26	318,6861	159,3431
Σ		199				75	3982,734	1072,594

• wartość średnia:

x_śr=(Σ x_i n_i /n) =0,376884≈ 0,377

• wariancja:

s²= (Σ(x_i-x_śr)²n_i)/n =5,389918≈ 5,390

• odchylenie średnie:

s=2,32162≈ 2,322

x_max= x_śr + 3s= 7,341743

x_min= x_śr - 3s=-6,58797

Wartości graniczne mieszczą się w wyznaczonych wyżej granicach.

4.Histogram:

5.Wykres dystrybuanty:

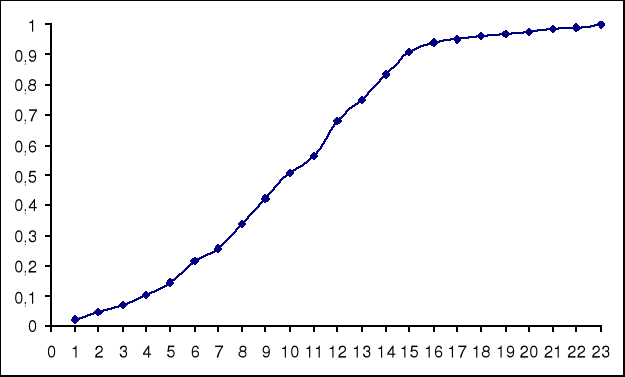
6.Granica rozrzutu dla poziomu ufności α= 0,95 to:

P(x_śr - t⋅s < x_śr < x_śr + t⋅s) = 0,95

2Φ = 0,95

Φ= 0,45

z tabel funkcji Laplace'a: t= 1,96

stąd t⋅s = 1,96 ⋅ 10^-3 ⋅2,322= 0,05

Δx= 1μm

s= 2,322 μm

n= (t² s²)/ Δx ²

n= (1,96² ⋅ 2,322²)/ 1²

n= 21,135≈22

nr	x	x- xśr	(x- xśr)^2
1	-9	-10,5	110,25
2	-8	-9,5	90,25
3	-7	-8,5	72,25
4	-6	-7,5	56,25
5	-5	-6,5	42,25
6	-4	-5,5	30,25
7	-3	-4,5	20,25
8	-2	-3,5	12,25
9	-1	-2,5	6,25
10	0	-1,5	2,25
11	1	-0,5	0,25
12	2	0,5	0,25
13	3	1,5	2,25
14	4	2,5	6,25
15	5	3,5	12,25
16	6	4,5	20,25
17	7	5,5	30,25
18	8	6,5	42,25
19	9	7,5	56,25
20	10	8,5	72,25
21	11	9,5	90,25
22	12	10,5	110,25
Σ	33		885,5

x_śr = 1,5

s² = 26,83

s= 5,18

7.Sprawdzamy za pomocą statystyk Grubbusa

B₁ = (x_max- x_śr)/ s ; B₁ ≈2,027

B₂ = (x_śr- x_min)/ s ; B₂ ≈ 2,027

B_kr = 2,664

B_kr >B₁

B_kr>B₂

Dla poziomu ufności 0,95 i k= n- 1=21 z tablic rozkładu Studenta wynika, że

t=1,721

t⋅s =8,9

0statecznie: 7,99 ± 0, 0089 μm

8.Statystyka Gosseta

nr pomiaru	przedział	n	x	x n	x-xsr	(x-xśr)^2
1	(-10,5;-9,5)	3	-9	-27	-9,377	87,926
2	(-9,5;-8,5)	5	-8	-40	-8,377	70,172
3	(-8,5;-7,5)	5	-7	-35	-7,377	54,418
4	(-7,5;-6,5)	6	-6	-36	-6,377	40,665
5	(-6,5;-5,5)	9	-5	-45	-5,377	28,911
6	(-5,5;-4,5)	14	-4	-56	-4,377	19,157
7	(-4,5;-3,5)	8	-3	-24	-3,377	11,403
8	(-3,5;-2,5)	16	-2	-32	-2,377	5,650
9	(-2,5;-1,5)	17	-1	-17	-1,377	1,896
10	(-1,5;0,5)	17	0	0	-0,377	0,142
11	(0,5; 1,5)	11	1	11	0,623	0,388
12	(1,5; 2,5)	23	2	46	1,623	2,635
13	(2,5; 3,5)	14	3	42	2,623	6,881
14	(3,5; 4,5)	17	4	68	3,623	13,127
15	(4,5; 5,5)	15	5	75	4,623	21,373
16	(5,5;6,5)	6	6	36	5,623	31,619
17	(6,5;7,5)	2	7	14	6,623	43,866
18	(7,5;8,5)	2	8	16	7,623	58,112
19	(8,5;9,5)	2	9	18	8,623	74,358
20	(9,5;10,5)	1	10	10	9,623	92,604
21	(10,5;11,5)	2	11	22	10,623	112,851
22	(11,5;12,5)	1	12	12	11,623	135,097
23	(12,5;13,5)	1	13	13	12,623	159,343
Σ		197		71	37,332

x_śr = 0,36

s=6,782

---