PRACOWNIA FIZYCZNA AKADEMII PODLASKIEJ |
|||
W SIEDLCACH |
|||
Adam Jędrych , III Matematyka |
2 Grupa |
||
Imię i Nazwisko, kierunek studiów |
|
||
21 d Nr ćwiczenia |
3.III.2003 Data wykonania |
Ocena zaliczenia |
Podpis |
Temat: Wyznaczanie ładunku i pojemności kondensatora.
Do wykonania ćwiczenia budujemy następujący obwód:
Przyrządy wykorzystywane w ćwiczeniu to:
woltomierz (V),
amperomierz (*A),
wyłącznik (W),
kondensator (C),
źródło prądu (E),
stoper.
Lp. |
t |
I |
U |
P |
Q |
C |
|
s |
*A |
V |
*C |
*C |
*F |
1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13. 14. 15. 16. 17. 18. 19. 20. 21. 22. 23. 24. 25. 26. 27. 28. 29. 30. 31. 32. 33. 34. 35. 36. 37. 38. 39. 40. 41. 42. 43. 44. 45. 46. 47. 48. 49. 50. 51. 52. 53. 54. 55. 56. 57. 58. 59. 60. 61. |
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 |
28 27 26,5 26 25,5 25 24,5 23,5 23 22,5 22 21,5 21 20 19,5 19 19 18,5 17,5 17,5 17 16,5 16 15,5 15 15 14,5 14 13,5 13,5 13 12,5 12 11,5 11,5 11,5 11 10,5 10,5 10 10 10 9,5 9 9 9 8,5 8,5 8 8 8 8 7,5 7 7 7 7 6,75 6,5 6,5 6,5 |
100 |
27,5 26,75 26,25 25,75 25,25 24,75 24 23,25 22,75 22,25 21,75 21,25 20,5 19,75 19,25 19 18,75 18 17,5 17,25 16,75 16,25 15,75 15,25 15 14,75 14,25 13,75 13,5 13,25 12,75 12,25 11,75 11,5 11,5 11,25 10,75 10,5 10,25 10 10 9,75 9,25 9 9 8,75 8,5 8,25 8 8 8 7,75 7,25 7 7 7 6,875 6,625 6,5 6,5
|
861,5 |
8,615 |
Sporządzam wykres zależności natężenia prądu rozładowania kondensatora od czasu I = f(t).
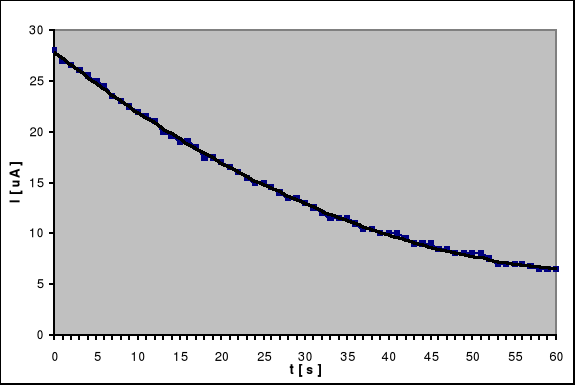
Celem doświadczenia jest wykonanie pomiaru ładunku elektrycznego metodą całkowania graficznego. Na wykresie przedstawiliśmy krzywą obrazującą zmianę prądu płynącego przez kondensator w zależności od funkcji czasu I = f(t). Krzywa ta jest krzywą miary prądu rozładowania kondensatora w czasie. Obszar pod otrzymaną krzywą podzieliliśmy na 60 trapezów, których pola obliczymy ze wzoru
![]()
P1 = [(28+27)/2]*1 = 27,5
P2 = [(27+26,5)/2]*1 = 26,75
......
......
P59 = [(6,5+6,5}/2]*1 = 6,5
P60 = [(6,5+6,5}/2]*1 = 6,5
![]()
Obliczamy Q tj. pole pod krzywą jako sumę pól 60 trapezów według wzoru:
Q = 861,5 μC
Obliczamy pojemność kondensatora.
C = Q / U
C = 861,5 [μC] /100 [V] = 8,615 μF
Obliczamy błędy wielkości mierzonych.
Δ U = 150 [V] * 0,5 / 100 = 0,75 V
Δ I = 75 [μA] * 0,5 /100 = 0,375 μA
Δ t = 0,2 s
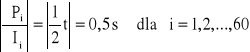
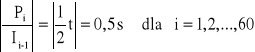
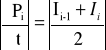
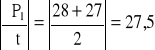
.....
.....
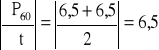
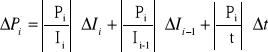
ΔP1 = 0,5*0,375+0,5*0,375+27,5*0,2=5,875
ΔP2 = 5,725
ΔP3 = 5,625
ΔP4 = 5,525
ΔP5 = 5,425
ΔP6 = 5,325
ΔP7 = 5,175
ΔP8 = 5,025
ΔP9 = 4,925
ΔP10= 4,825
ΔP11= 4,725
ΔP12= 4,625
ΔP13= 4,475
ΔP14= 4,325
ΔP15= 4,225
ΔP16= 4,175
ΔP17= 4,125
ΔP18= 3,975
ΔP19= 3,875
ΔP20= 3,825
ΔP21= 3,725
ΔP22= 3,625
ΔP23= 3,525
ΔP24= 3,425
ΔP25= 3,375
ΔP26= 3,325
ΔP27= 3,225
ΔP28= 3,125
ΔP29= 3,075
ΔP30= 3,025
ΔP31= 2,925
ΔP32= 2,825
ΔP33= 2,725
ΔP34= 2,675
ΔP35= 2,675
ΔP36= 2,625
ΔP37= 2,525
ΔP38= 2,475
ΔP39= 2,425
ΔP40= 2,375
ΔP41= 2,375
ΔP42= 2,325
ΔP43= 2,225
ΔP44= 2,175
ΔP45= 2,175
ΔP46= 2,125
ΔP47= 2,075
ΔP48= 2,025
ΔP49= 1,975
ΔP50= 1,975
ΔP51= 1,975
ΔP52= 1,925
ΔP53= 1,825
ΔP54= 1,775
ΔP55= 1,775
ΔP56= 1,775
ΔP57= 1,750
ΔP58= 1,7
ΔP59= 1,675
ΔP60= 1,675
![]()
Obliczamy błędy wielkości szukanej (pojemności kondensatora).
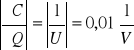
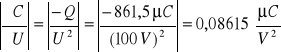
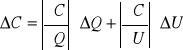
ΔC = 0,01 [1/V] * 194,8 [μC] + 0,08615 [μC/V2] * 0,75 [V] = 1,948 [μC/V] +
+ 0,065 [μC/V] = 2,013 [μC/V]
C = ( 8,615 ± 2,013 ) [μC/V]
Wnioski
Celem doświadczenia był pomiar ładunku elektrycznego kondensatora. W tym celu wyznaczyliśmy krzywą obrazującą zmianę prądu płynącego przez kondensator w funkcji czasu I = f(t). Tę krzywą nazywamy krzywą miary prądu rozładowania kondensatora w czasie. Ładunek zgromadzony na kondensatorze i pojemność tego kondensatora wyznaczamy przez pomiar natężenia prądu rozładowania. Najpierw kondensator zostaje naładowany do różnicy potencjałów. Następnie przez otwarcie wyłącznika znajdującego się w obwodzie powodujemy odpływ ładunku w kondensatorze przez opór R i jego rozładowanie. Ze względu na to, że napięcie pomiędzy okładkami maleje zmniejsza się również natężenie prądu przepływającego przez opornik. Można zauważyć, że wraz z upływem czasu natężenie prądu maleje dążąc do 0. Wówczas kondensator ulega rozładowaniu. Proces ten przedstawia krzywa prądu rozładowania stanowiąca podstawę do obliczania ładunku, który zgromadził się na okładkach kondensatora. W naszym przypadku wynosi ono
Q = ( 861,5 ± 194,8 ) [μC]
Wartość ta pozwoliła uzyskać w dalszych obliczeniach pojemność kondensatora użytego w doświadczeniu.
C = ( 8,615 ± 2,013 ) [μF]
Otrzymana wartość pojemności kondensatora obarczona jest błędem, na który składa się błąd pomiaru natężenia jak również opóźnione ludzkie reakcje (włączanie i wyłączanie stopera, odczyt z amperomierza).
![]()
![]()
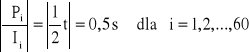
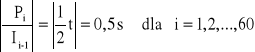
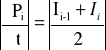
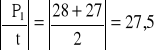
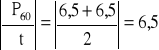
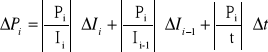
![]()
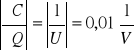
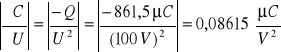
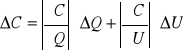
Wyszukiwarka