POLITECHNIKA CZĘSTOCHOWSKA

WYDZIAŁ ELEKTRYCZNY

Laboratorium Zakłóceń w Układach Elektroenergetycznych

Temat: Badanie obwodów trójfazowych

Wykonał:

Dróżdż Tomasz

Sekret Tomasz

Studia magisterskie

Niestacjonarne

Semestr I

Częstochowa 2011/2012

1. Cel ćwiczenia

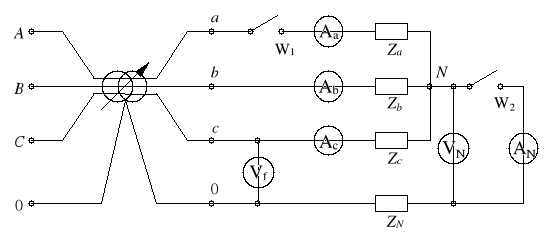
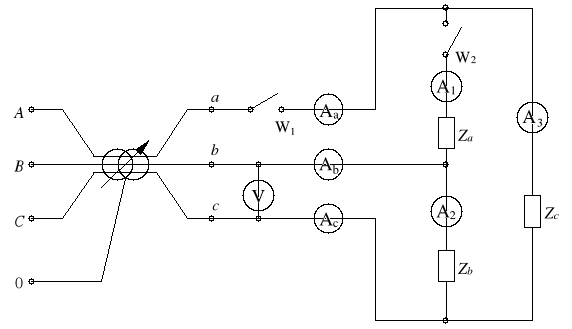
Celem ćwiczenia jest zapoznanie się z własnościami obwodów trójfazowych symetrycznych i niesymetrycznych, ich wykresami topograficznymi oraz zjawiskami zachodzącymi w tych obwodach w przypadku istnienia różnych asymetrii.

2. Część teoretyczna

Układem trójfazowym nazywamy zbiór obwodów elektrycznych, w których działają napięcia źródłowe sinusoidalnie zmienne jednakowej częstotliwości, przesunięte względem siebie w fazie i wytwarzane w jednym źródle energii, zwanym prądnicą lub generatorem trójfazowym.

Układy trójfazowe dzielą się na:

• symetryczne i niesymetryczne,

Obwód 3-fazowy symetryczny jest to układ złożony z prądnicy 3-fazowej wytwarzającej trzy napięcia źródłowe symetryczne linii zasilającej o jednakowych impedancjach oraz trzech odbiorników energii o jednakowych impedancjach zespolonych

• układy zrównoważone i niezrównoważone.

Obwód 3-fazowy nazywamy zrównoważonym jeżeli moc chwilowa pobrana przez wszystkie fazy odbiornika jest wielkością stałą niezależną od czasu. (Układ symetryczny jest zrównoważony).

W układzie trójfazowym symetrycznym przy połączeniu odbiornika w gwiazdę:

• potencjał punktu zerowego źródła jest równy potencjałowi punktu zerowego odbiornika,

• suma wartości skutecznych zespolonych napięć fazowych odbiornika jest równa zeru,

• moduły prądów przewodowych we wszystkich fazach są jednakowe,

• suma wartości skutecznych zespolonych prądów przewodowych jest równa zeru,

• moduł napięcia międzyfazowego U_p jest
  razy większy od modułu napięcia fazowego U_f

• moc pobierana przez odbiornik jest równa potrójnej wartości mocy pobieranej przez jedną fazę.

W układzie trójfazowym symetrycznym przy połączeniu odbiornika w trójkąt:

• moduły prądów fazowych płynących w gałęziach trójkąta są jednakowe,

• suma wartości skutecznych zespolonych prądów fazowych jest równa zeru,

• moduł prądu przewodowego I_p jest
  razy większy od modułu prądu fazowego I_f:

3. Schematy pomiarowe

• Schemat do pomiaru w układzie gwiazdowym

• Pomiary w układzie trójkątowym

Dla różnych położeń wyłączników W₁ i W₂ oraz przy różnych obciążeniach dokonano pomiarów napięć i prądów.

Lp.	Układ połączeń	Prze­wód zero­wy	W1	W2	Impedancje				Pomiary						Obliczenia
										Za	Zb	Zc	ZN	Uf	UN	IA	IB	IC	IN	UN	IA	IB	IC	IN	SA	SB	SC	S
														V	V	A	A	A	A	V	A	A	A	A	VA	VA	VA	VA
1		symetryczny	jest	Z	Z				RN	92	0	1,5	1,5	1,5	0	0	1,6	1,6	1,6	0	147,2	147,2	147,2	441
2			brak	Z	O					92	0	1,5	1,5	1,5	0	0	1,6	1,6	1,6	0	147,2	147,2	147,2	441
3		przerwa w fazie A	jest	O	Z					92	0	0	1,5	1,5	1,5	0	0	1,6	1,6	1,6	0	120	120	240
4			brak	O	O					92	47	0	1,5	1,5	0	49	0	1,6	1,6	0	0	100	100	200
5	zwarcie fazy A	brak	Z	O	0				92	90	3,4	2	2	0	89	3,6	2,1	2,1	0	140	80	80	300
6	niesymetryczny (Za  Zb  Zc, ZN = 0)	jest	Z	Z				0	92	0	1,5	1,2	1,2	1	0	1,6	1,1	1,1	1,1	36	22	22	80
7			brak	Z	O					92	64	2	1,1	1	0	67	2,2	1,3	1,1	0	110	80	70	260
8	(Za = Zb  Zc, ZN  0)	jest	Z	Z				RN	92	0	1,5	1,5	1	3	0	1,6	1,6	1,2	4	90	90	60	240

4. Tabele pomiarowe

• Tabela 1 (dla odbiornika gwiazdowego)

Z - zamknięty, O - otwarty

Dane: R = 55  (dla U_f = 85 V), L = 0,11 H, C = 40 F, Z_N = j79,6 

Tabela 1 (dla odbiornika gwiazdowego)

Lp.

Układ połączeń

Prze­wód zero­wy

W1

W2

Impedancje

Pomiary

Obliczenia

Za

Zb

Zc

ZN

Uf

UN

IA

IB

IC

IN

UN

IA

IB

IC

IN

SA

SB

SC

S









V

V

A

A

A

A

V

A

A

A

A

VA

VA

VA

VA

1

symetryczny

jest

Z

Z

R

R

R

RN

94

0

1,5

1,5

1,5

0

2

brak

Z

O

R

R

R

∞

94

0

1,5

1,5

1,5

0

3

przerwa w fazie A

jest

O

Z

∞

R

R

RN

94

0

0

1,4

1,5

1,5

4

brak

O

O

∞

R

R

∞

94

46

0

1,3

1,5

0

5

zwarcie fazy A

brak

Z

O

0

R

R

∞

92

90

3,4

2

2

0

6

niesymetryczny (Za ≠ Zb ≠ Zc, ZN = 0)

jest

Z

Z

R

L

C

0

92

232

1,9

4,3

3,9

0

8

(Za = Zb ≠ Zc, ZN ≠ 0)

jest

Z

Z

R

R

C

RN

92

0

1,5

1,2

1,2

3,5

Lp.	Układ połączeń	W1	W2	Impedancje			Pomiary							Obliczenia
								Za	Zb	Zc	U	I1	I2	I3	IA	IB	IC	I1	I2	I3	IA	IB	IC	SA	SB	SC	S
											V	A	A	A	A	A	A	A	A	A	A	A	A	VA	VA	VA	VA
1	symetryczny	Z	Z				92	2	2	1,8	3,4	3,4	3,4	1,3	1,3	1,3	2,4	2,4	2,4	119	119	119	358
2	przerwa w linii A	O	Z	R	R	R	44	1,4	2	1,4	0	3,4	3,4	1,8	2,2	1,8	0	2,7	2,7	0	260	260	520
3	przerwa w fazie A	Z	O		R	R	92	0	2	1.8	2	2	2	0	2,2	2,1	2,1	2,1	2,1	200	184	165	540
4	niesymetryczny	Z	Z				92	2	2	2	1,4	1,3	2,2	2,1	2,1	2,1	1,5	1,4	2,4	92	87	141	320

Z - zamknięty, O - otwarty

Dane: R = 66  (dla U = 105 V), L = 0,11 H, C = 40 F

Tabela 2 (dla odbiornika trójkątowego)

Lp.

Układ połączeń

W1

W2

Impedancje

Pomiary

Obliczenia

Za

Zb

Zc

U

I1

I2

I3

IA

IB

IC

I1

I2

I3

IA

IB

IC

SA

SB

SC

S







V

A

A

A

A

A

A

A

A

A

A

A

A

VA

VA

VA

VA

1

symetryczny

Z

Z

R

R

R

160

3,4

3,4

3,4

2

2

2

2

przerwa w linii A

O

Z

R

R

R

80

0

3,3

3,4

1,3

2

1,4

3

przerwa w fazie A

Z

O

∞

R

R

160

2

1,9

3,4

0

2

2

4

niesymetryczny

Z

Z

R

L

C

160

4

4,1

2,3

2

2,4

2,05




5. Obliczenia

E_a = 92 V

E_b = 92e^-j120 = -46-j78 V

E_c = 92e^j120 = -46+j78 V

V_a = E_a V_b = E_b V_c = E_c

Jako Z przyjmujemy 55e^j0 dla 85V

J_a = =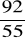
= 1,6 A

J_b = =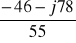
= -0,8-j1,73 = 1,6e^-j120 A

J_c = =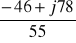
= -0,8+j1,73 = 1,6e^j120 A

J_N = J_a+J_b+J_c = 1,6-0,8-j1,73-0,8+j1,73 = 0 A

S_a = V_aJ_a* = 921,6 = 147,2 VA

S_b = V_bJ_b = (-46-j78) 1,6 = 147,2 VA

S_c = V_cJ_c = (-46+j78) 1,6 = 147,2 VA

S = S_a+S_b+S_c = 3147,2 = 441,6 VA

U₁ = 92e^j0 = 92 V

U₂ = 92e^-j120 = -46-j75 V

U₃ = 92e^j120 = -46+j75 V

I_a = =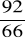
= 1,3 A

I_b = =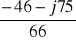
= -0,6-j2,5 A

I_c = =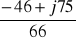
= -0,6+j2,5 A

J_a = I_a - I_c = 1,3+0,6-j2,5 = 1,9-j2,5 = 2,4e^-29 A

J_b = I_b - I_a = -0,6-j2,5-1,3 = -1,9-j2,5 = 2,4e^-j149 A

J_c = I_c - I_b = -0,6+j2,5+1,3+j2,5 = 2,4e^j91 A

S₁ = U₁I_a* = 921,3 = 119 VA

S = S₁+S₂+S₃ = 3119 = 358 VA

6. Wnioski

Przy symetrycznym odbiorze układu gwiazdowego z przewodem N , prądy każdej fazy są sobie równe dlatego też nie płyną żadne prądy wyrównawcze . Gdy wyłączymy jedną żarówkę , otrzymamy obciążenie niesymetryczne charakteryzujące się pojawieniem prądów w przewodzie N . Im większy prąd będzie płyną przez jedną z faz tym większy będzie prąd I_N Oczywiście przy idealnym przewodzie zerowym Z_n jest równa zero. W rzeczywistości Z_n zawiera się od zera do nieskończoności i na ogół dobrze jest znać jej wartość . Impedancja powinna być bliska zeru co określałoby w miarę dokładnie działający obwód . Przy zmianie wielkości obciążenia zaobserwowaliśmy ciągłą zmianę nie tylko prądu ale także napięcia . Jeżeli jedna z faz będzie bez obciążenia to prąd w tej gałęzi nie będzie płyną . Co uzyskaliśmy z pomiarów , a uzasadnione to jest z Prawa Ohma . Przy połączeniu symetrycznym układ zachowuje się tak samo z przewodem zerowym jak i bez niego . Wprowadzając asymetrię obciążenia różnica prądów będzie tylko widoczna w przewodach fazowych .

Układ trójkątny objęty jest innymi zależnościami . Po pierwsze nie mamy doczynienia z przewodem N , nie płyną więc prądy wyrównawcze . Każdy prąd przewodowy jest pierwiastek z trzech większy od prądu fazowego . Napięcia są sobie równe . Każdy prąd fazowy jest sumą poszczególnych prądów przewodowych , zgodnie z Prawem Kirchoffa . Przy symetrycznym obciążeniu w każdej gałęzi mamy takie same wartości prądów i napięć . Przy braku symetrii np. zwiększając impedancję obwodu z żarówkami automatycznie zmniejszamy prąd fazowy , a także prąd przewodu . Można wywnioskować , że każdy rodzaj obciążenia , ma swoje charakterystyczne cechy . Porównując otrzymane pomiary z wartościami wliczonymi otrzymujemy w niektórych przypadkach znaczne różnice . Powodem tych różnic jest zbyt mała precyzja działania przyrządów , np. niedokładne sprzęganie autotransformatorów , czyli powstawanie różnic przesunięć kątowych na każdą fazę .. Różnice w wynikach są też spowodowane nieidealnym zachowaniem się odbiorników np. żarówka oprócz rezystancji , posiada jeszcze pewną indukcyjność.

---