Nr. Ćwiczenia:	Temat: Badanie rozkładu Gaussa
Data wykonania:	Data oddania:	Data poprawy:	Ocena:

1.WSTĘP TEORETYCZNY.

Rozkład zmiennej losowej x to rozkład prawdopodobieństwa, w którym zmienna losowa przyjmuje określone wartości. Jeżeli zmienna jest dyskretna, to podlega rozkładowi dyskretnemu (skokowemu). Gdy przyjmujemy wartości dowolne lub ciągłe, to podlega rozkładowi ciągłemu. Zmienną losową mogą być wyniki pomiarów.

Różne graficzne sposoby przedstawiania pomiarów. Oś odciętych to wartość pomiaru, a na osi rzędnych jest liczba pomiarów lub gęstość prawdopodobieństwa.

Z punktu widzenia statystyki, najważniejszym rozkładem ciągłym jest rozkład normalny. Został on wprowadzony przez Laplace'a (1783) oraz niezależnie przez Gaussa (1794). Gęstość prawdopodobieństwa dla tego rozkładu zwanego zazwyczaj rozkładem Gaussa określa wzór:

G, (x, n,

exp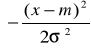
,

gdzie:

n - liczba pomiarów,

x - liczba rzeczywista,

m - wartość oczekiwana równa z dużą dokładnością średniej wartości pomiaru
:

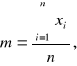
- odchylenie standardowe:

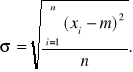
Rozkładem Gaussa można opisać szereg zależności występujących w przyrodzie np. rozkład wzrostu czy masy osobników mających tyle samo lat, rozkład masy ziaren grochu, masy liści z danego drzewa, błędów itd. Jest to krzywa, którą najczęściej wykorzystujemy opisując zjawiska statystyczne.

2.PRZEBIEG DOŚWIADZCZENIA:

W opisywanym doświadczeniu ważymy na wadze analitycznej 250 ziaren grochu pochodzącego z jednej plantacji. W tym przypadku opracowując ćwiczenie wykorzystywać będziemy histogram. Jest to taki sposób przedstawienia wyników, w którym kolejne wartości grupujemy w przedziałach zwanych klasami. Praktyka pokazuje, że najwięcej informacji uzyskujemy rysując histogram z liczbą klas - k, spełniającą nierówność:

gdzie n jest liczbą pomiarów.

Znając liczbę klas obliczmy rozstęp danych R:

R =
_max
min

oraz „szerokość” klasy:

W ćwiczeniu na osi y, wstępnie odkładać będziemy liczbę zdarzeń (pomiarów) w danej klasie. Od liczby zdarzeń do prawdopodobieństwa przechodzimy dzieląc liczbę zdarzeń w danym przedziale przez liczbę wszystkich zdarzeń.W pierwszej fazie przedstawiamy otrzymane wyniki w postaci histogramu, gdzie na osi x odkładamy masy ważonych ziaren, a na osi y ich liczbę. W drugiej fazie sporządzamy histogram, dla którego na osi y odkładamy prawdopodobieństwa zdarzeń:

,

gdzie n jest liczbą wszystkich zdarzeń.

Po wyliczeniu wartości średniej:

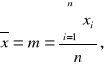
oraz odchylenia standardowego:

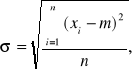
wykreślamy krzywą Gaussa.

3. WYNIKI I ICH OPRACOWANIE:

Waga 250 ziarenek wraz z pudełkiem - 203,132g

Waga 250 ziarenek bez pudełka - 68,197g

Klasy:

7,91<k<15,81

n - 250 ziarenek

Rozstęp:

R =
_max
min

R=0,404-0,119

R=0,285

Szerokość klasy:

b₁=0,029 g

b₂=0,014 g

Prawdopodobieństwo zdarzeń:

,

Przedział	Zdarzenie	Prawdopodobieństwo
0,1 -0,119	1	0,004
0,12 -0,139	1	0,004
0,14 - 0,159	2	0,008
0,16 - 0,179	6	0,024
0,18 - 0,199	10	0,04
0,2 - 0,219	16	0,064
0,22 - 0,239	25	0,1
0,24 - 0,259	35	0,14
0,26 - 0,279	43	0,172
0,28 - 0,299	33	0,132
0,3 - 0,319	29	0,116
0,32 - 0,339	25	0,1
0,34 - 0,359	14	0,056
0,36 - 0,379	6	0,024
0,38 - 0,399	3	0,012
0,4 - 0,419	1	0,004

Wartość średnia:

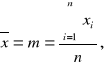
m=0,272

Odchylenie standardowe:

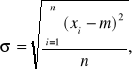
=0,002682=0,003

=(0,272±0,003) - zakres błędu

Krzywa Gaussa:

Zdarzenie	Prawdopodobieństwo
1	0,004
1	0,004
2	0,008
6	0,024
10	0,04
16	0,064
25	0,1
35	0,14
43	0,172
33	0,132
29	0,116
25	0,1
14	0,056
6	0,024
3	0,012
1	0,004

4. Podsumowanie:

Z obliczeń w naszym doświadczeniu wynika że ważąc ziarenka mogliśmy pomylić się na każdym z nich o 0,003g. Krzywa Gaussa to doskonały sposób do dokładnego obliczania w tak szerokim zakresie prób, jakim są badane przez nas ziarenka grochu.

---