Piotr Wiśniewski 15.XI.2002
Ćwiczenie 44
Temat: Badanie prawa Ohma dla obwodu całkowitego.
Wyniki :
Wyniki wartości napięć dla rosnących natężeń prądu :
Lp. |
I [A] |
U [V] |
1 |
1,5 |
12,75 |
2 |
1,7 |
12,68 |
3 |
1,9 |
12,65 |
4 |
2,1 |
12,62 |
5 |
2,3 |
12,59 |
6 |
2,5 |
12,56 |
7 |
2,7 |
12,53 |
8 |
2,85 |
12,51 |
9 |
8 |
12,49 |
Wyniki wartości napięć dla malejących natężeń prądu :
Lp. |
I [A] |
U [V] |
1 |
3 |
12,49 |
2 |
2,85 |
12,5 |
3 |
2,7 |
12,51 |
4 |
2,5 |
12,52 |
5 |
2,3 |
12,54 |
6 |
2,1 |
12,56 |
7 |
1,9 |
12,57 |
8 |
1,7 |
12,59 |
9 |
1,5 |
12,61 |
Teoria :
Każdy przewodnik umieszczony w obwodzie prądu elektrycznego stawia opór przepływającemu w nim prądowi. Oznacza to, że każdy przewodnik posiada cechę go charakteryzująca, którą jest opór elektryczny.
I prawo Ohma :
Dla każdego przewodnika stosunek napięcia przyłożonego do końców tego przewodnika do prądu przez niego przepływającego jest wielkością stałą, którą nazywamy oporem elektrycznym. Matematycznie prawo to opisane jest wzorem ![]()
.
II prawo Ohma :
Opór danego przewodnika jest uzależniony od jego geometrycznych rozmiarów oraz od rodzaju materiału z jakiego został wykonany. ![]()
gdzie S - przekrój przewodnika, l - długość, p - opór właściwy (charakteryzujący dany materiał).
Z obwodami elektrycznymi ściśle związane są dwa prawa Kirchhoffa.
I prawo Kirchhoffa:
Suma algebraiczna natężeń prądów wpływających i wypływających w węźle jest równa 0. Matematycznie można to zapisać wzorem ![]()
np. ![]()
II prawo Kirchhoffa:
Suma algebraiczna sił elektromotorycznych wewnątrz dowolnego obwodu zamkniętego jest równa sumie iloczynów natężenia prądów i oporów elektrycznych w różnych częściach tego obwodu.
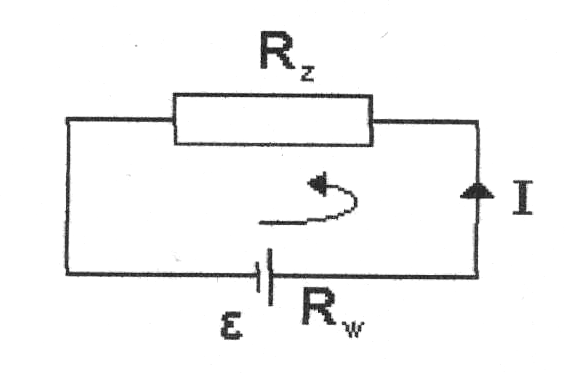
Korzystając z zależności zachodzących w takim obwodzie można wyprowadzić wzory pozwalające określić wielkość siły elektromotorycznej źródła. Można określać ją różnymi metodami:
a) pomiar prądu w obwodzie
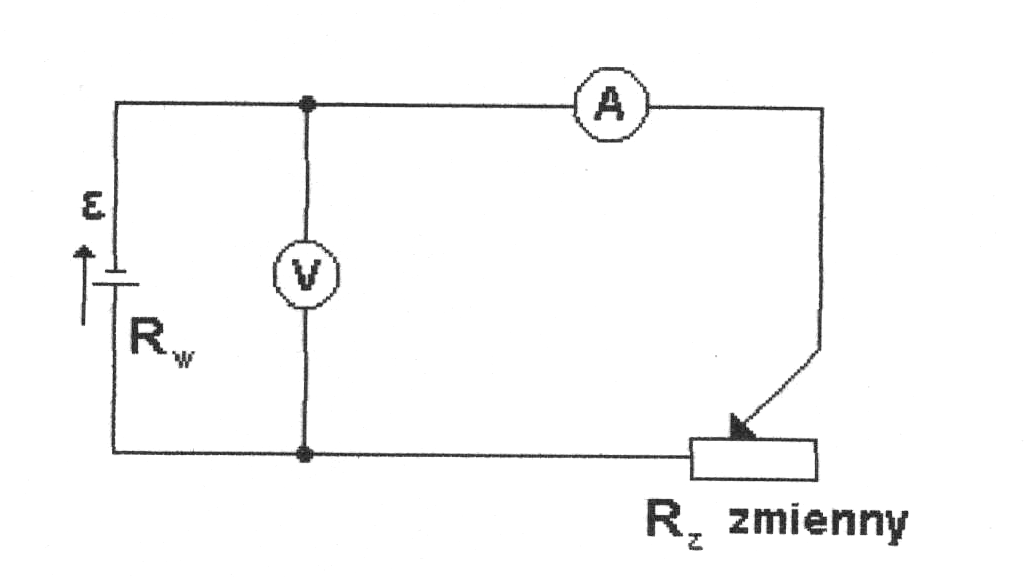
![]()
![]()
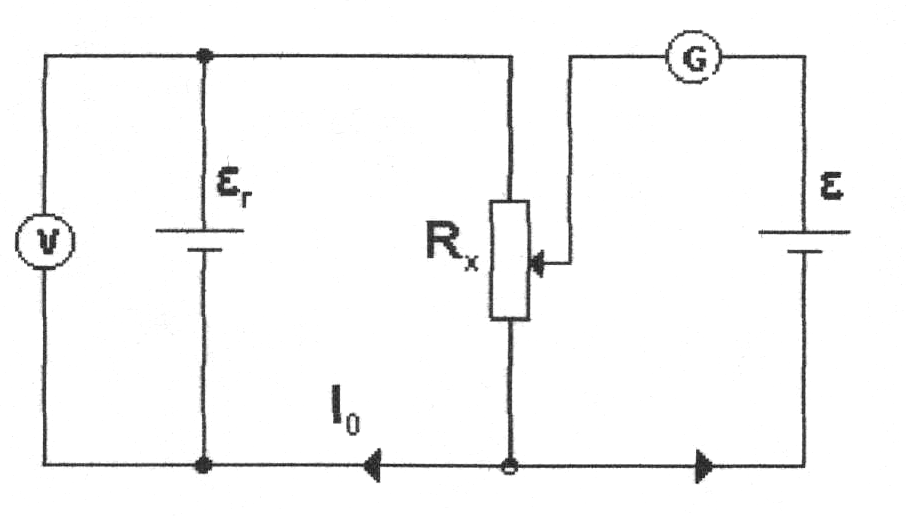
b) metoda bezprądowa (kompensacyjna)
![]()
- źródło siły elektromotorycznej o znanych parametrach korzystając z II prawa Kirchhoffa ![]()
Regulując suwakiem doprowadzamy do takiego stanu by przez galwanometr nie płynął prąd. Wówczas prąd z badanego źródła nie płynie i nie występuje spadek napięcia na jego rezystancji wewnętrznej. ![]()
Jeżeli prąd nie płynie , to ![]()
![]()
![]()
Obliczenia :
Obliczamy wartość SEM i rezystencji wewnętrznej metodą najmniejszych kwadratów :
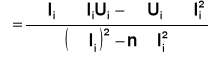
i 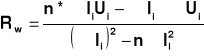
Wyniki dla pomiaru wartości napięć dla rosnących natężeń prądu :
E=12,67812 V
Rw= 0,028301![]()
Wyniki dla pomiaru wartości napięć dla malejących natężeń prądu :
E= 12,72527 V
Rw= 0,07968 ![]()
Obliczanie niepewności :
Wykonując pomiary dwu wielkości x i y uzyskujemy pary liczb (xi, yi) i naszym zadaniem jest znaleźć równanie prostej najlepiej „pasującej” do nich. Niech równanie to będzie miało postać:
y = a * x + b
a „dopasowanie” zgodnie z metodą najmniejszych kwadratów oznacza, że:
![]()
gdzie a i b są empirycznymi współczynnikami regresji liniowej, Poszukując ekstremum związanego powyższego równania udowadnia się, że:
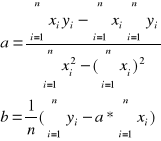
gdzie i = 1,2,3,4,...,n czyli n jest ilością par punktów (xi, yi).

Na odchylenie standardowe S(a) i S(b) będące miarą niepewności pomiarowych współczynników regresji a i b otrzymuje się następujące równania:
Kryterium tego jak punkty pomiarowe (xi, yi) potwierdzają liniową zależność pomiędzy wielkościami x i y, stanowi wartość tzw. współczynnika korelacji liniowej p. Jego wartość zmienia się w granicach od 1 do 0. Gdy p=1, to dopasowanie jest idealne. Gdy p=0, to zależność liniowa pomiędzy xi i yi nie istnieje.
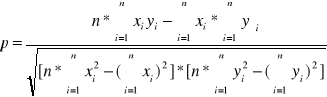
Niepewności pomiarowe parametrów akumulatora oblicza się z wzorów
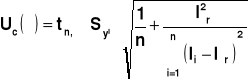
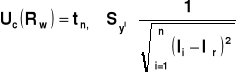
gdzie ![]()
współczynnik rozszerzenia
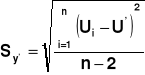
![]()
- punkty wyznaczone w oparciu o równania prostych Niepewność pomiarowa :
Po dokonaniu obliczeń otrzymujemy następujące wyniki:
A) równanie prostej :
dla natężeń rosnących
a = 0,225428 b = 11,95781
y = a * x + b = 0,225428 * x + 11,95781
dla natężeń malejących
a = 0,182051 b = 12,12765
y = a * x + b = 0,182051 * x + 12,12765
Niepewności pomiarowe akumulatora :
dla natężeń rosnących
![]()
![]()
dla natężeń malejących
![]()
![]()
Wyniki ostateczne
-- dla natężeń rosnących :
![]()
![]()
-- dla natężeń malejących :
![]()
![]()
Wnioski :
Wyniki z doświadczenia pomogły nam obliczyć parametry charakteryzujące źródło energii elektrycznej, czyli siłę elektromotoryczną i rezystancję wewnętrzną. Wyniki trochę się różnią, co wynika z faktu, że akumulator (źródło naszego prądu) trochę się wyczerpał i miał trochę mniejsze napięcie przed pierwszym pomiarem, inne przed drugim pomiarem i inne (mniejsze) po wykonaniu wszystkich pomiarów.
Doświadczenie z jabłkami:
Opis doświadczenia:
Do jednego jabłka wkładamy drut żelazny i drut miedziany. Badamy napięcie dotykając końcówkami Voltomierza obu drutów. Napięcie dla jednego jabłka wynosi 0,58 V. Jeżeli podłączyliśmy dwa jabłka szeregowo to napięcie było równe 1,21 V , a jeżeli trzy jabłka szeregowo to napięcie wyniosło 1,71 V. Jeżeli trzy jabłka podłączyliśmy równolegle to napięcie wyniosło 0,21 V.
W połączeniu szeregowym stosujemy wzór:
![]()
W połączeniu równoległym stosujemy wzór:
![]()
Badaliśmy też natężenie prądu dla jednego jabłka - 0,08 A - i dla dwóch jabłek połączonych szeregowo - 0,16 A. Stosujemy tu podobne wzory co do napięcia.
Teoria:
Zasada budowy ogniwa Volty typu Zn/Cu oraz ilustracja konsekwencji istnienia szeregu napięciowego metali dla ogniw. Bateria jest to zestaw połączonych ogniw. Napięcie elektryczne między końcowymi elektrodami ogniw połączonych szeregowo jest określone iloczynem liczby ogniw i napięcia pojedynczego ogniwa. Zjawisko to zostało odkryte przez Voltę około 1800 roku. Skonstruował on „wieniec kubeczków” oraz stos zawierający szereg połączonych płytek cynkowo-srebrnych. Pomiędzy płytkami umieszczony został papier nasycony wodą morską. W ten sposób uzyskał baterię o napięciu około 180V (nazwa jednostki pochodzi od jego nazwiska). W bateriach wykorzystywane są ogniwa Volty i Leclanchego.
Dostępne w handlu ogniwa oznaczone symbolami R6, R14, R20 są „suchymi” ogniwami Leclanchego. Powszechnie używana ich nazwa - „baterie” jest błędna, ponieważ oznacza ona zespół ogniw połączonych szeregowo lub równolegle. Baterią we właściwym tego słowa znaczeniu jest na przykład tzw. bateria płaska (4.5V), zbudowana z trzech ogniw suchych połączonych szeregowo.
Ogniwo Leclanchego jest stale udoskonalane i obecnie na rynku znajduje się szereg jego modyfikacji, charakteryzujących się lepszymi parametrami użytkowymi. Należą do nich między innymi tzw. alkaliczne ogniwa Leclanchego o większej pojemności niż ogniwa klasyczne.

Szereg elektrochemiczny
Nazwa pierwiastka |
Symbol pierwiastka |
Potencjał |
Lit |
Li |
-3,00V |
Rubid |
Rb |
-2,97V |
Potas |
K |
-2,92V |
Rad |
Ra |
-2,92V |
Bar |
Ba |
-2,90V |
Stront |
Sr |
-2,89V |
Wapń |
Ca |
-2,84V |
Sód |
Na |
-2,71V |
Lantan |
La |
-2,52V |
Magnez |
Mg |
-2,38V |
Itr |
Y |
-2,37V |
Beryl |
Be |
-1,70V |
Glin |
Al |
-1,66V |
Niob |
Nb |
-1,1V |
Mangan |
Mn |
-1,05V |
Cynk |
Zn |
-0,76V |
Chrom |
Cr |
-0,71V |
Gal |
Ga |
-0,56V |
Żelazo |
Fe |
-0,44V |
Kadm |
Cd |
-0,40V |
Tal |
Tl |
-0,33V |
Ind |
In |
-0,33V |
Kobalt |
Co |
-0,28V |
Nikiel |
Ni |
-0,24V |
Molibden |
Mo |
-0,20V |
Cyna |
Sn |
-0,14V |
Ołów |
Pb |
-0,13V |
Wodór |
H |
0V |
Antymon |
Sb |
+0,2V |
Bizmut |
Bi |
+0,23V |
Miedź |
Cu |
+0,37V |
Ruten |
Ru |
+0,45V |
Srebro |
Ag |
+0,8V |
Osm |
Os |
+0,85V |
Rtęć |
Hg |
+0,85V |
Pallad |
Pd |
+0,85V |
Iryd |
Ir |
+1,15V |
Platyna |
Pt |
+1,2V |
Złoto |
Au |
+1,42V |
Wnioski:
Posługując się trzema jabłkami połączonymi szeregowo udało nam się zbudować baterię o pojemności około 1,5 V. Powtórzyliśmy w pewien sposób doświadczenie Volty. Zamiast jabłek możemy użyć także innych przedmiotów np. innych jabłek (cytryn). Wystarczy tylko aby materiały (pierwiastki) z jakich zostały wykonane druty miały różne wartości w szeregu elektrochemicznym metali (u nas żelazo i miedz).
1
5
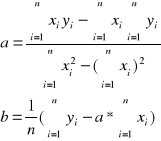
![]()

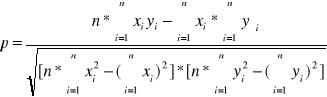
Wyszukiwarka