3. Elementy kinematyki pŁynÓw

3.1. Opis ruchu płynu

Przedmiotem kinematyki płynów jest ustalenie ogólnych praw ruchu płynu względem danego układu odniesienia. Zakładając, że ruch płynu jest każdorazowo dany, zajmiemy się analizą kinematycznych wielkości charakteryzujących zachowanie się dowolnie wybranej cząstki płynu.

Dysponujemy dwiema podstawowymi metodami pozwalającymi opisać ruch płynu: metodą Lagrange'a i metodą Eulera.

Metoda Lagrange'a opiera się na badaniu ruchu wybranej cząstki płynu. Jeżeli przez
oznaczymy współrzędne dowolnego elementu płynu w chwili początkowej
, a przez
jego współrzędne kartezjańskie, to położenie elementu w dowolnej chwili t będzie określone równaniami:

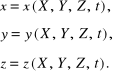
(3.1)

Składowe wektora prędkości
elementu wyznaczają pierwsze pochodne cząstkowe względem czasu:

(3.2)

zaś składowe wektora przyspieszenia
drugie pochodne cząstkowe względem czasu:

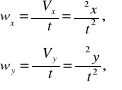
(3.3)

(3.3cd.)

Stan kinematyczny płynu będzie znany, gdy będą dane równania (3.1) ÷ (3.3) dla wszystkich elementów płynu.

Metoda Eulera polega na badaniu ruchu płynu w określonych punktach przestrzeni i tylko pośrednio zajmuje się ruchem indywidualnego elementu płynu. Istotę tej metody stanowi badanie pól wielkości fizycznych (rozdz. 1.4) i w wyniku jej zastosowania otrzymuje się - najczęściej wykorzystywany - opis ruchu płynu w postaci funkcji (1.16) lub (1.18).

W mechanice płynów rozważamy często zmiany zachodzące w pewnej masie płynu. Wyodrębnioną masę płynu nazywa się obszarem płynnym , jeśli two-rzą ją wciąż te same elementy płynne lub też obszarem kontrolnym , jeśli tworzą ją wciąż te same punkty przestrzenne, natomiast znajdują się w niej, w miarę upływu czasu, coraz to inne elementy płynu.

Zamkniętą powierzchnię ograniczającą obszar płynny nazywamy powierz-chnią płynną; podobnie powierzchnię ograniczającą obszar kontrolny nazywamy powierzchnią kontrolną .

3.2. Graficzna reprezentacja pola prędkości

Niech będzie dane pole wektora prędkości płynu:

(3.4)

Linie tego pola wektorowego (styczne w każdym swym punkcie do wektora pola) nazywają się liniami prądu .

Oznaczając element linii prądu przez
, równanie linii prądu możemy napisać w postaci iloczynu wektorowego

(3.5)

lub też w postaci równoważnej

(3.6)

W równaniach (3.5) ÷ (3.6) czas t odgrywa rolę parametru; kształt linii prądu zależy więc od czasu i tylko w ustalonym polu prędkości będzie niezmienny.

Powierzchnia prądu jest to powierzchnia utworzona z linii prądu, przecinających dowolną linię, nie będącą linią prądu. Jeśli ta dowolna linia jest zamknięta, powierzchnia prądu bywa nazywana rurką prądu .

Linia, po której porusza się pojedynczy element płynu nazywa się torem ele-mentu ; jest ona graficzną reprezentacją matematycznego opisu ruchu Lagrange'a.

Równanie torów elementów płynu otrzymujemy wychodząc z definicji wektora prędkości. Oznaczając element toru przez
, możemy napisać równanie różniczkowe toru w następującej postaci

(3.7)

albo po przekształceniu

(3.8)

Między równaniami (3.6) i (3.8) zachodzi istotna różnica; w równaniu (3.8) czas nie jest stałym parametrem, ale zmienną.

Chwilowy obraz linii, łączącej wszystkie cząstki płynu, które wyszły z jednego źródła i przeszły przez ten sam punkt pola nazywa się linią wysnutą . Linię ta-ką wyznaczają elementy płynu odróżniającego się wizualnie od tła dostarczone do pola przepływu w określonym punkcie przestrzeni (np. dym w powietrzu lub atrament w wodzie, wypływające z dyszy do obszaru przepływu płynu); w ustalonym polu prędkości jest ona zarazem linią prądu i torem każdego elementu płynu, przechodzącego przez ten punkt.

3.3. Przyspieszenie elementu płynu

Przyspieszenie elementu płynu, traktowanego jako punkt, jest pochodną prędkości elementu względem czasu, wyraża się zatem wzorem

(3.9)

Zgodnie z regułami różniczkowania, różniczka zupełna
prędkości

jest określona następująco

i po wykorzystaniu wzorów (3.8) otrzymamy

(3.10)

Przy zastosowaniu operatora Hamiltona

wzór (3.10) możemy przepisać w postaci

(3.11)

gdzie

(3.12)

Równość (3.11) orzeka, że przyspieszenie elementu płynu, wyrażone pochod-ną substancjalną prędkości
jest sumą pochodnej lokalnej
oraz pochodnej konwekcyjnej
Nazwy tych pochodnych wynikają z ich sensu fizycznego. Mianowicie pochodna
określa zmiany zachodzące w poruszającym się, ale wciąż tym samym elemencie płynu, tzn. zmiany dotyczące jego substancji; pochodna lokalna określa zmiany zachodzące z upływem czasu w stałym punkcie przestrzeni; pochodna konwekcyjna określa zmiany prędkości związane z samym tylko przesunięciem elementu płynu w inne położenie.

Pojęcia pochodnej substancjalnej, lokalnej i konwekcyjnej są pojęciami ogólnymi i mogą być odniesione do dowolnych funkcji (1.18) - opisujących całą klasę wielkości fizycznych. Wobec tego można wprowadzić pojęcie operatora różniczkowania materialnego

, (3.13)

nazywanego często operatorem Stokesa .

3.4. Różniczkowe równanie ciągłości

Równanie ciągłości jest podstawowym równaniem mechaniki płynów, wynikającym z zasady zachowania masy i wyrażającym ciągły charakter przepływu.

Załóżmy, że ruch płynu został określony za pomocą pola prędkości (3.4) i pola gęstości płynu

(3.14)

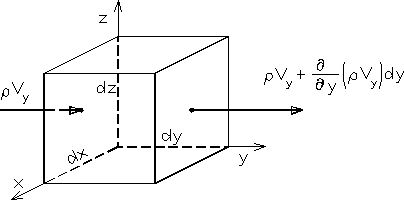
Rys. 3.1

W przestrzeni wypełnionej poruszającym się płynem wyodrębniamy obszar kon-trolny w kształcie prostopadłościanu o bokach
(rys. 3.1).

Masa płynu zawarta w obszarze kontrolnym może się zmieniać z upływem czasu wskutek dwu przyczyn:

- zmiany gęstości płynu,

- dopływu przez ściankę powierzchni kontrolnej.

Jeśli w czasie t gęstość wynosiła
to w czasie
gęstość będzie równa

zatem zmiana masy płynu wynikająca ze zmiany jego gęstości wyniesie

(3.15)

Masa płynu przepływającego przez jednostkową powierzchnię w jednostce czasu jest równa iloczynowi jego gęstości i prędkości. Obliczymy masy płynu: wpływającą i wypływającą w czasie
do obszaru kontrolnego przez powierzchnie o bokach
i
(rys. 3.1):

- masa wpływająca

- masa wypływająca

Różnica tych wielkości jest następująca

Jeśli uwzględnimy przepływy przez pozostałe powierzchnie obszaru kontrolnego i porównamy je ze zmianą masy reprezentowaną wzorem (3.15), otrzymamy równanie ciągłości przepływu

(3.16)

Przy wykorzystaniu operatora diwergencji równanie (3.16) można zapisać w po-staci

(3.17)

a stąd, po wykonaniu różniczkowania i wprowadzeniu pochodnej substancjalnej (3.13), dostajemy

(3.18)

Dla ruchu stacjonarnego oraz cieczy równanie ciągłości upraszcza się do następujących postaci:

(3.19)

(3.20)

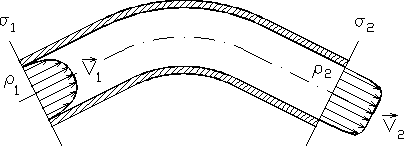
Rys. 3.2

W niektórych działach stosowanej mechaniki płynów przyjmuje się jednowymiarowość i stacjonarność przepływu jako podstawowe założenia upraszczające i wtedy stosujemy szczególne formy równania ciągłości. W celu uzyskania tych form równania ciągłości rozważymy ruch płynu przez kanał ograniczony ściankami kontrolnymi
i
(rys. 3.2).

Zdefiniujemy pojęcie średniej prędkości normalnej w przekroju σ

(3.21)

Masa płynu zawarta wewnątrz kanału musi być stała, a więc masa płynu dopływającego musi być równa masie płynu odpływającego. Zakładając, że gęstość płynu nie zmienia się w dowolnym przekroju poprzecznym otrzymamy

,

tzn, że strumień masy przepływającej przez dowolny przekrój poprzeczny kanału, zwany wydatkiem masowym albo masowym natężeniem prze-pływu , jest stały

(3.22)

Dla cieczy zależność (3.22) upraszcza się do postaci

(3.23)

w której stała Q nazywana jest wydatkiem objętościowym albo obję-tościowym natężeniem przepływu .

3.5. Struktura pola prędkości płynu

Rozpatrzmy ruch lokalny płynu, rozumiany jako ruch punktów elementu płynu względem bieguna, dowolnie wybranego w rozpatrywanym elemencie.

Z całej masy poruszającego się płynu wycinamy myślowo element objętościowy w kształcie prostopadłościanu o krawędziach
(rys. 3.3). Położenie tego elementu odpowiada pewnej chwili t; z upływem czasu element przesuwa się względem układu odniesienia, przy czym może on również zmieniać swój kształt.

Rozważać będziemy ruch punktu M względem bieguna A. Wektor prędkości
w punkcie M będzie równy wektorowi prędkości
w punkcie A powiększonemu o jego różniczkę zupełną

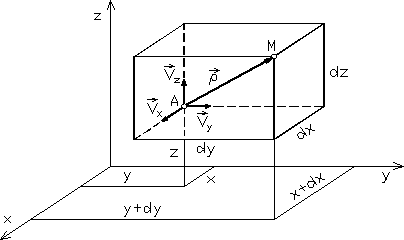
Rys. 3.3

składowe prędkości w punkcie M będą zatem wyrażać się wzorami:

Do prawych stron powyższych równań dodamy i odejmiemy kolejno następujące wielkości:

i następnie, po przekształceniach, zapiszemy składowe prędkości punktu M za pomocą wzorów:

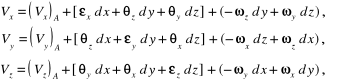
(3.24)

w których dla zwięzłości zapisu wprowadzono oznaczenia:

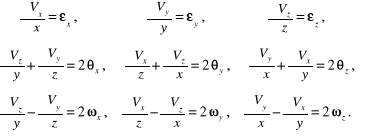
(3.25)

Postaramy się obecnie wykazać, że wielkości (3.25) odpowiadają określonym odkształceniom i obrotowi elementu płynu przedstawionego na rysunku 3.3.

Jeśli różne od zera będą tylko wielkości wtedy boki elementu ulegną wydłużeniu lub skróceniu, a element pozostanie po odkształceniu prostopadłościanem. Oznacza to, że składowe te odpowiadają odkształceniom objętościowym, a zmiana objętości w czasie
wyrazi się wzorem

(3.26)

Wprowadzając pojęcie prędkości właściwej odkształcenia objętościowego, zdefiniowanej jako stosunek przyrostu objętości (3.26) do objętości początkowej i czasu, w którym ten przyrost nastąpił, otrzymamy

(3.27)

Załóżmy obecnie, że znikają wszystkie wielkości (3.25) oprócz . Wynika stąd zależność
i ze wzoru (3.24) mamy:

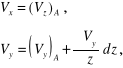
Element prostopadłościenny odkształcony zgodnie z powyższymi wzorami jest pokazany na rysunku 3.4. Wskutek różnic prędkości prostokąt ABCD odkształci się, przyjmując po upływie czasu
kształt równoległoboku AB'C'D'. Bok AB obróci się dookoła osi x o kąt
a bok AD o kąt
w związku z tym kąt prosty DAB zmniejszy się o wielkość
Wykorzystując rys. 3.4 łatwo obliczamy:

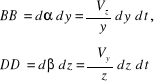
i następnie otrzymujemy

(3.28)

wielkości odpowiadają więc odkształceniom postaciowym elementu płynu.

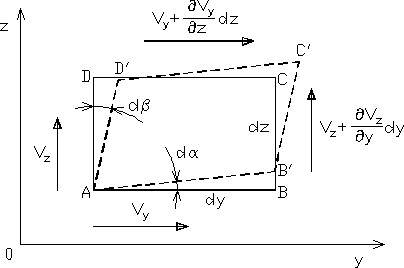
Rys. 3.4

Na koniec załóżmy, że w wyrażeniach określających składowe prędkości (3.24) znikają wszystkie wielkości występujące w nawiasach kwadratowych; element płynu nie doznaje więc ani odkształceń objętościowych, ani też odkształceń postaciowych - jest zatem ciałem sztywnym.

Niech

będzie wektorem prędkości kątowej obrotu takiego elementu płynu wokół chwilowej osi przechodzącej przez biegun A, a

wektorem określającym położenie każdego jego punktu względem bieguna. Składowe prędkości każdego punktu elementu, wyznaczone ze wzoru

wyrażają się więc wzorami:

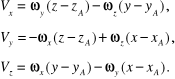
Obliczając następnie wektor
otrzymujemy zależność

(3.29)

z której wynikają oznaczenia różnic pochodnych zastosowane we wzorach (3.25).

Reasumując, stwierdzamy, że wektor prędkości przemieszczenia dowolnego punktu płynu (3.24) składa się w ogólnym przypadku z prędkości postępowej bieguna
, prędkości od obrotu elementu jako ciała sztywnego wokół osi przechodzącej przez biegun (wyrazy w nawiasach okrągłych) oraz prędkości deformacji objętościowych i postaciowych elementu (wyrazy w nawiasach kwadratowych); jest to pierwsze twierdzenie Helmholtza .

3.6. Pojęcia i twierdzenia dotyczące p*l wirowych

Ruchem wirowym płynu nazywamy taki ruch, którego pole prędkości spełnia warunek

(3.30)

Zgodnie ze wzorami (3.24), elementy płynu mogą doznawać obrotów wokół osi własnych, a prędkość kątowa może tworzyć w ogólnym przypadku niestacjonarne pole wektorowe:

(3.31)

Wektorowa linia pola prędkości kątowej
nazywana jest linią wirową. Jest to linia styczna do wektorów prędkości kątowych elementów płynu, które znajdują się na niej w danej chwili (rys. 3.5).

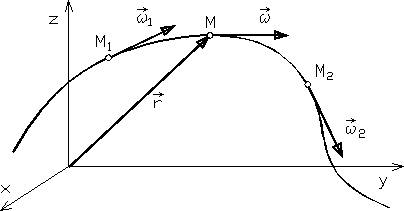
Rys. 3.5

Równanie różniczkowe linii wirowej jest analogiczne do równania linii prądu (3.5) ÷ (3.6):

(3.32)

w którym wektor
jest elementem linii wirowej.

Analogicznie do pojęcia powierzchni prądu i rurki prądu wprowadza się pojęcie powierzchni wirowej i rurki wirowej, jako powierzchni składającej się z linii wirowych, przecinających dowolną linię zamkniętą, nie będącą linią wirową.

Obliczymy teraz strumień rotacji przez dowolny przekrój poprzeczny rurki wirowej (rys. 3.6). Linia leżąca na rurce wirowej stanowi krawędź powierzchni utworzonej z powierzchni bocznej i przekroju poprzecznego rurki wirowej σ, którego brzegiem jest linia l.

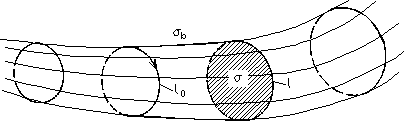
Rys. 3.6

Zgodnie z definicją linii wirowych strumień rotacji przez powierzchnię jest równy zeru; zatem z twierdzenia Stokesa otrzymujemy

(3.33)

57

---