WYDZIAŁ ELEKTRYCZNY

STUDIA MAGISTERSKIE UZUPEŁNIAJĄCE

LABORATORIUM ZAKŁÓCEŃ W UKŁADACHELEKTROENERGETYCZNYCH

Badanie obwodów trójfazowych

Semestr: I

Rok: I

Madejak Andrzej

1. Cel ćwiczenia

Celem ćwiczenia jest zapoznanie się z właściwościami układów trójfazowych symetrycznych i niesymetrycznych, ich wykresami wskazowymi oraz zjawiskami zachodzącymi w tych układach w przypadkach różnych rodzajów niesymetrii obciążenia, jak i zasilania.

2. Spis przyrządów pomiarowych

• walizka pomiarowa QN-10

• woltomierz elektromagnetyczny prądu przemiennego, pozycja pracy pozioma, klasa dokładności 1, sprawdzony napięciem probierczym 2 kV, nr 06155

• amperomierz elektromagnetyczny prądu przemiennego, pozycja pracy pozioma, klasa dokładności 0,5 ; sprawdzony napięciem probierczym 2 kV, nr 303492

• amperomierz elektromagnetyczny prądu przemiennego, pozycja pracy pozioma, klasa dokładności 0,5 ; sprawdzony napięciem probierczym 2 kV, nr 303365

• amperomierz elektromagnetyczny prądu przemiennego, pozycja pracy pozioma, klasa dokładności 0,5 ; sprawdzony napięciem probierczym 2 kV, nr 0711.91

• Impedancje: Z_a = Z_b = Z_c = 55 Ω, Z_N = j79,6 Ω - połączenie w gwiazdę

• Impedancje: Z_a = Z_b = Z_c = 66 Ω - połączenie w trójkąt

3. Schematy układów pomiarowych

Wyznaczanie kolejności faz w układzie trójfazowym

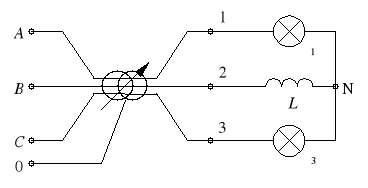
Schemat układu trójfazowego połączonego w gwiazdę

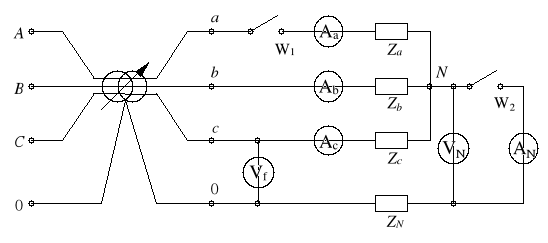
Schemat układu trójfazowego połączonego w trójkąt

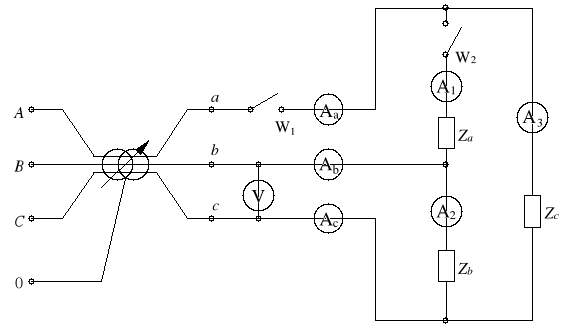
4. Tabele pomiarów

Wyznaczanie kolejności faz

Faza	Odbiornik	I [A]	U [V]
L1	Ż1	1	80	Słabo świeci
L2	L	2	80	Dławik
L3	Ż3	1,4	150	Mocno świeci

Faza	Odbiornik	I [A]	U [V]
L3	Ż1	1	150	Mocno świeci
L2	L	2	80	Dławik
L1	Ż3	1,4	80	Słabo świeci

Żarówka 1 świeci mocniej niż żarówka 3, zaciski 1, 2, 3 tworzą układ trójfazowy kolejności zgodnej i można je oznaczyć A, B, C. Natomiast gdy żarówka 1 świeci słabiej niż żarówka 3, układ 1, 2, 3 jest kolejności przeciwnej i zaciski można oznaczyć jako A, C, B

Pomiary w układzie połączeń w gwiazdę

L.p.

Układ połączeń

Przewód zerowy

Pozycje wyłącznika

Obciążenie

Z pomiarów

ZA

ZB

ZC

Zn

Uf

UN

IN

IA

IB

IC

W1

W2

V

V

A

A

A

A

1

symetryczny

jest

Z

Z

R

R

R

L

86

0

0,1

1,4

1,4

1,4

brak

Z

O

R

R

R

∞

86

0

0

1,4

1,4

1,3

2

przerwa w fazie A

jest

O

Z

∞

R

R

L

86

35

0

0

1,3

1,2

brak

O

O

∞

R

R

∞

86

0

0

0

1,2

1,2

3

zwarcie fazy A

brak

Z

O

O

R

R

∞

86

0

0

4,5

2,7

2,7

4

niesymetryczny

jest

Z

Z

R

L

C

0

66

0

1,2

1,6

1,4

1,7

brak

Z

O

R

L

C

∞

64

0

0

1,5

1,3

2,4

jest

Z

Z

R

R

C

L

64

0

0

1,4

1,2

2,4

Z - pozycja wyłącznika zamknięta

O - pozycja wyłącznika otwarta

L.p.	Układ połączeń	Przewód zerowy	Pozycje wyłącznika		Z obliczeń
										UN	IN	IA	IB	IC	SA	SB	SC	S
						W1	W2	V	A	A	A	A	VA	VA	VA	VA
		1	symetryczny	jest	Z	Z	0	0	1,5	1,5	1,5	223,4	223,4	223,4	670,3
				brak	Z	O	-	0	1,5	1,5	1,5	223,4	223,4	223,4	670,3
		2	przerwa w fazie A	jest	O	Z	26,8	0,34	-	1,5	1,28	0	223,4	90,24	313,64
				brak	O	O	0	0	0	1,3	1,3	0	190	190	380
3	zwarcie fazy A	brak	Z	O	86	0	4,3	2,5	2,5	640	372,5	372,5	1385
4	niesymetryczny	jest	Z	Z	0	1,1	1,5	1,4	1,7	223,5	208,6	253,3	685,4
				brak	Z	O	0	0	1,5	1,4	2,2	223,5	208,6	327,8	759,9
				jest	Z	Z	55	0,33	1,5	1,3	2,2	223,5	193,7	327,8	745

Z - pozycja wyłącznika zamknięta

O - pozycja wyłącznika otwarta

Pomiary w układzie połączeń w trójkąt

Lp.	Układ połączeń	Pozycje wyłącznika		Obciążenia			z pomiarów
								Z1	Z2	Z3	U	I1	I2	I3	IA	IB	IC
				W2	W3							V	A	A	A	A	A	A
1	symetryczny	Z	Z	R	R	R	200	2,2	2,2	2,2	3,6	3,6	3,6
2	przerwa w linii „A”	O	Z	R	R	R	190	1,6	2,2	2,2	0	3,6	3,6
3	przerwa w fazie „A”	Z	O	∞	R	R	190	0	2,2	2,2	2,2	2,2	3,6
4	niesymetryczny	Z	Z	R	L	C	190	2,2	2,6	2,6	1,7	1,4	3

Z - pozycja wyłącznika zamknięta

O - pozycja wyłącznika otwarta

Pomiary w układzie połączeń w trójkąt

Lp.	Układ połączeń	Pozycje wyłącznika		Obciążenia			z obliczeń
								Z1	Z2	Z3	I1	I2	I3	IA	IB	IC	SA	SB	SC	S
				W2	W3							A	A	A	A	A	A	VA	VA	VA	VA
1	symetryczny	Z	Z	R	R	R	2,9	2,9	2,9	4,9	4,9	4,9	933	933	933	2800
2	przerwa w linii „a”	O	Z	R	R	R	2,3	2,8	2,8	0	4,9	4,9	0	933	933	1867
3	przerwa w fazie „A”	Z	O	∞	R	R	0	2,8	2,8	2,8	2,8	4,9	533	533	933	2000
4	niesymetryczny	Z	Z	R	L	C	2,9	3,3	3,3	3	2,7	4,3	572	514	819	1905

Z - pozycja wyłącznika zamknięta

O - pozycja wyłącznika otwarta

5. Obliczenia

Dla układu połączonego w gwiazdę (układ symetryczny)

Napięcia fazowe

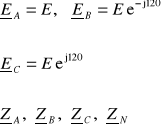
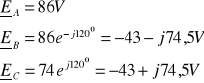
Potencjał punktu N

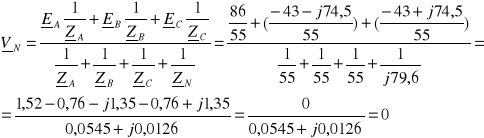
Spadki napięć na impedancjach odbiornika

Prądy fazowe

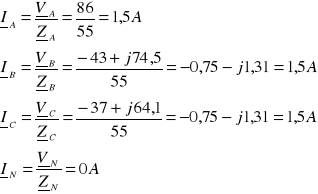
Napięcia liniowe

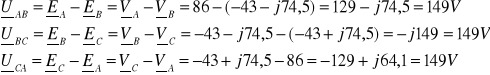
Przy układzie symetrycznym do wyznaczenia napięć liniowych możemy posłużyć się uproszczonym wzorem:

Wówczas:

Moc w układzie

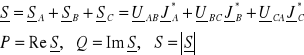
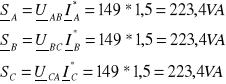
Dla układu połączonego w trójkąt (układ symetryczny)

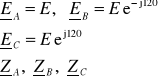
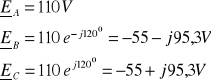
W przypadku układu symetrycznego moduł napięcia liniowego wynosi:

Tak, więc:

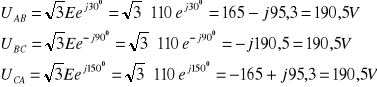
Prądy fazowe odbiornika obliczamy ze wzoru:

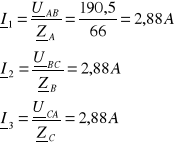
Prądy liniowe:

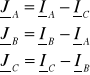
Ponieważ rozpatrujemy układ symetryczny, możemy posłużyć się zależnością:

W pozostałych przypadkach:

Moc w układzie analogicznie jak w przypadku układu gwiazdowego, tzn.:

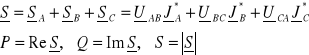
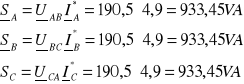
6. Wnioski

W przeprowadzonym ćwiczeniu zapoznaliśmy się z własnościami obwodów trójfazowych symetrycznych i niesymetrycznych. Obserwowaliśmy zjawiska zachodzące w tych obwodach w przypadku zaistnienia asymetrii napięć podczas obciążenia w układzie trójfazowym.

Zjawiska w obwodach prądu zmiennego są związane ze zmianami pola elektrycznego i magnetycznego. Przy zmiennych napięciach i prądach, pola elektryczne i magnetyczne również są zmienne. Energia pola elektrycznego przekształca się w energię pola magnetycznego i na odwrót. Podczas wykonywania pomiarów prąd w przewodzie zerowym układu symetrycznego gwiazdowego nie płynie. Napięcie w punkcie zerowym jest również równe zero.

W przypadku gdy występuje przerwa w fazie „a” i podłączony jest przewód zerowy to prądy w przewodach „b” i „c” nie zmieniają się, natomiast prąd gałęzi „a” jest równy zero.

W układzie trójkątowym symetrycznym zarówno prądy przewodowe jak i fazowe są równe. Moce pobierane przez poszczególne fazy również są sobie równe. Gdy występuje przerwa w zasilaniu którejś z faz wówczas prąd przewodowy tej fazy jest równy zero.

Przy symetrycznym odbiorze układu gwiazdowego z przewodem N, prądy każdej fazy są sobie równe dlatego też nie płyną żadne prądy wyrównawcze. Gdy odłączymy jeden z odbiorników, otrzymamy obciążenie niesymetryczne charakteryzujące się pojawieniem prądów w przewodzie N. Im większy prąd będzie płyną przez jedną z faz tym większy będzie prąd I_N. Oczywiście przy idealnym przewodzie zerowym, Z_n jest równa zero, my nie mogliśmy tego uwzględnić przy naszych obliczeniach, gdyż porównywane wartości pomiarowe były obarczone dużym błędem bezwzględnym. W rzeczywistości Z_n zawiera się od zera do nieskończoności i na ogół dobrze jest znać jej wartość. Impedancja powinna być bliska zeru co określałoby w miarę dokładnie działający obwód . Przy zmianie wielkości obciążenia zaobserwowaliśmy ciągłą zmianę nie tylko prądu ale także napięcia . Jeżeli jedna z faz będzie bez obciążenia to prąd w tej gałęź nie będzie płyną. Co uzyskaliśmy z pomiarów, a uzasadnione to jest z prawa Ohma. Przy połączeniu symetrycznym układ zachowuje się tak samo z przewodem zerowym jak i bez niego . Wprowadzając asymetrię obciążenia różnica prądów będzie tylko widoczna w przewodach fazowych. Przy obciążeniu RLC obwód zachowuje się tak samo jak wcześniej. Gdybyśmy chcieli otrzymać obciążenie symetryczne musielibyśmy z większą dokładnością dobierać wartości RLC aby otrzymać takie same impedancje w gałęziach.

Układ trójkątny objęty jest innymi zależnościami. Po pierwsze nie mamy do czynienia z przewodem N, nie płyną więc prądy wyrównawcze. Każdy prąd przewodowy jest pierwiastek z trzech większy od prądu fazowego. Napięcia są obie równe. Każdy prąd fazowy jest sumą poszczególnych prądów przewodowych, zgodnie z Prawem Kirchoffa. Przy symetrycznym obciążeniu w każdej gałęzi mamy takie same wartości prądów i napięć. Przy braku symetrii np. zwiększając impedancję obwodu z żarówkami automatycznie zmniejszamy prąd fazowy, a także prąd przewodu. Można wywnioskować, że każdy rodzaj obciążenia, ma swoje charakterystyczne cechy. Porównując otrzymane pomiary z wartościami wliczonymi otrzymujemy w niektórych przypadkach znaczne różnice . Powodem tych różnic jest zbyt mała precyzja działania przyrządów, np. niedokładne sprzęganie autotransformatorów, czyli powstawanie różnic przesunięć kątowych na każdą fazę. Możemy tez wziąć pod uwagę małą precyzyjność pomiarową . Mierzyliśmy bowiem , w niektórych przypadkach prądy rzędu dziesiątek ampera. Różnice w wynikach są też spowodowane nieidealnym zachowaniem się odbiorników które nie są idealne i oprócz rezystancji, posiada jeszcze pewną indukcyjność .

Na koniec można zwrócić uwagę na następujące sytuacje:

• w układzie linii trójfazowych, w których jedna faza jest bardziej obciążona mają większe spadki napięcia niż linie trójfazowe równomiernie obciążone

• można zauważyć gdy w linii trójfazowej występuje duża asymetria obciążeń to zużycie mocy w układzie elektroenergetycznym dla tzw. „potrzeb własnych” może w skrajnie niekorzystnych warunkach wzrosnąć siedmiokrotnie w stosunku do wielkości zużycia mocy w tej sieć, podczas obciążenia symetrycznego

• duże obciążenie symetryczne faz może doprowadzić do tzw. ujemnego spadku napięcia w fazie, która jest najmniej obciążona. Może to doprowadzić do takiej sytuacji, że napięcie na końcu obwodu będzie wyższe, niż początku obwodu.

POLITECHNIKA CZĘSTOCHOWSKA 2012

POLITECHNIKA CZĘSTOCHOWSKA 2012

---