RACHUNEK RÓŻNICZKOWY FUNKCJI JEDNEJ ZMIENNEJ CZ.2
Definicja 1. (zbiór wypukły)
![]()
- wypukły wtedy i tylko wtedy, gdy
![]()
odcinek o końcach x1, x2 jest zawarty w ![]()
.
Inaczej mówiąc, jeżeli potrafimy pokazać taki odcinek, którego końce należą do zbioru ![]()
, a on sam nie zawiera się w tym zbiorze, to ![]()
nie jest zbiorem wypukłym.
Definicja 2. (wypukłość funkcji)
Funkcja y = f (x) jest wypukła ku górze w ![]()
wtedy i tylko wtedy, gdy:
![]()
Funkcja y = f(x) jest wypukła ku dołowi w przedziale w ![]()
wtedy i tylko wtedy, gdy:
![]()
Zauważmy, że y = f(x0) + f'(x0)(x-x0) jest to równanie stycznej do wykresu funkcji w punkcie (x0,f(x0)), więc powyższą definicję można rozumieć tak:
Funkcja y = f(x) jest wypukła ku górze w ![]()
wtedy i tylko wtedy, gdy wykres funkcji w tym przedziale leży powyżej stycznej poprowadzonej w dowolnym punkcie o odciętej x0∈ ![]()
.
Funkcja y = f(x) jest wypukła ku dołowi w ![]()
wtedy i tylko wtedy, gdy wykres funkcji w tym przedziale leży poniżej stycznej poprowadzonej w dowolnym punkcie o odciętej x0∈ ![]()
.
Definicja 3. (punkt przegięcia)
Punkt (x0, f(x0)) jest punktem przegięcia wykresu funkcji y = f(x) wtedy i tylko wtedy, gdy przy przejściu przez ten punkt zmienia się wypukłość funkcji.
Inaczej: (x0, f(x0)) jest punktem przegięcia wtedy i tylko wtedy, gdy
![]()
f -wypukła ku górze
i jednocześnie ![]()
f -wypukła ku dołowi
lub
![]()
f -wypukła ku dołowi
i jednocześnie ![]()
f -wypukła ku górze.
Definicja 4. (ekstremum lokalne)
Niech ![]()
- otoczenie punktu ![]()
o promieniu ![]()
.
![]()
=![]()
.
Funkcja f(x) ma w punkcie x0 maksimum lokalne, jeśli
![]()
![]()
takie, że ![]()
![]()
mamy ![]()
Funkcja f(x) ma w punkcie x0 minimum lokalne, jeśli
![]()
![]()
takie, że ![]()
![]()
mamy ![]()
.
Definicja 5.
Drugą pochodną funkcji ![]()
w punkcie ![]()
nazywamy pochodną pierwszej pochodnej funkcji ![]()
w punkcie ![]()
i oznaczamy ![]()
.
Czyli:
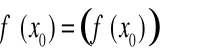
.
Uwaga.
Kolejne pochodne funkcji ![]()
w punkcie ![]()
definiujemy następująco:
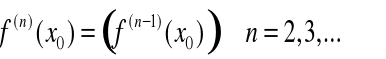
Definicja 6.
Przestrzeń funkcji ciągłych i n razy różniczkowalnych w sposób ciągły w przedziale ![]()
oznaczamy:
![]()
Badanie monotoniczności funkcji.
Niech funkcja ![]()
![]()
.
Wówczas:
Jeśli ![]()
, to funkcja rośnie w tym przedziale.
Jeśli ![]()
, to funkcja maleje w tym przedziale.
Jeśli ![]()
,to funkcja jest stała w tym przedziale.
Badanie wypukłości funkcji.
Jeżeli ![]()
i ![]()
, to funkcja jest wypukła ku górze w ![]()
.
Jeżeli ![]()
i ![]()
, to funkcja jest wypukła ku ku dołowi w ![]()
.
Warunek konieczny istnienia ekstremum
funkcji w punkcie.
Funkcja ciągła ![]()
ma w punkcie ![]()
minimum lub maksimum lokalne, jeśli ![]()
nie istnieje lub ![]()
.
Badanie istnienia ekstremów lokalnych funkcji.
Niech ![]()
i ![]()
.
Metoda porównywania znaków pochodnej
Jeśli ![]()
,
to funkcja ![]()
ma w punkcie ![]()
maksimum lokalne.
(tzn. jeśli pierwsza pochodna zmienia znak z „+” na „-” przy „przejściu” przez punkt ![]()
).
Jeśli ![]()
,
to funkcja ![]()
ma w punkcie ![]()
maksimum lokalne.
(tzn. jeśli pierwsza pochodna zmienia znak z „-” na „+” przy „przejściu” przez punkt ![]()
).
Metodę porównywania znaków pochodnej można zastosować również do tych wartości ![]()
, w których pochodna nie istnieje.
Metoda pochodnych wyższych rzędów.
Jeśli ![]()
, to ![]()
ma minimum lokalne w punkcie ![]()
.
Jeśli ![]()
, to ![]()
ma maksimum lokalne w punkcie ![]()
.
Jeśli natomiast okaże się, że ![]()
, to obliczamy kolejne pochodne ![]()
aż dojdziemy do takiej pochodnej, która w punkcie ![]()
nie równa się zeru.
Jeśli pierwszą z pochodnych różnych od zera jest pochodna ![]()
gdzie ![]()
liczba parzysta, to funkcja ![]()
ma w punkcie ![]()
minimum lokalne, gdy ![]()
, a maksimum lokalne gdy ![]()
.
Badanie istnienia ekstremów globalnych funkcji.
Aby znaleźć największą i najmniejszą wartość funkcji w danym przedziale ![]()
, obliczamy wszystkie jej maksima i minima lokalne wewnątrz tego przedziału, a także obliczamy wartości funkcji na końcach przedziału, w punktach nieciągłości funkcji i w punktach nieciągłości jej pochodnej.
Następnie ustalamy, która z obliczonych wartości jest największa, a która najmniejsza.
Warunek konieczny istnienia punktu przegięcia.
Funkcja ![]()
ma w ![]()
punkt przegięcia, jeśli ![]()
nie istnieje lub ![]()
.
Badanie istnienia punktów przegięcia.
Jeśli ![]()
i pierwsza pochodna nie zmienia znaku przy „przejściu” przez punkt ![]()
, to funkcja ma w ![]()
punkt przegięcia, w którym styczna jest równoległa do osi ![]()
.
Niech teraz ![]()
i ![]()
.
Metoda porównywania znaków pochodnej
Jeśli
![]()
lub
![]()
,
to funkcja ![]()
ma w ![]()
punkt przegięcia.
Tzn. jeśli druga pochodna zmienia znak z „+” na „-” lub z „-” na „+” przy „przejściu” przez punkt ![]()
, wówczas zmieni się także kierunek wypukłości krzywej, to mamy w ![]()
punkt przegięcia.
Metodę porównywania znaków pochodnej można zastosować również do tych wartości ![]()
, w których druga pochodna nie istnieje.
Metoda pochodnych wyższych rzędów.
Jeśli ![]()
oraz ![]()
, to funkcja ![]()
ma w ![]()
punkt przegięcia.
Jeśli natomiast okaże się, że również ![]()
, to obliczamy kolejne pochodne ![]()
aż dojdziemy do takiej pochodnej, która w punkcie ![]()
nie równa się zeru.
Wówczas jeżeli pierwsza różniąca się od zera pochodna będzie rzędu nieparzystego, to w ![]()
jest punkt przegięcia.
A'
x'
x”
f(x)
y=f(x0)+f'(x0)(x-x0)
x0
b
a
y
x
x
y
a
b
x0
y=f(x0)+f'(x0)(x-x0)
f(x)
p.p.
p.p.
y
x
Wyszukiwarka