Laboratorium Mechaniki
Wydział Transportu		Imię i nazwisko		Ocena
					Bartosz Głowacki Karol Gorzoch Rafał Gasiorowski Tomasz Karolak Konrad Jędrzejczyk
Rok Akademicki 2000/2001	Grupa T2
Ćwiczenie nr 6 Temat : Wpływ Karbu na rozkład naprężeń przy obciążeniu statycznym
Data wykonania ćwiczenia 02.04.2001			Data oddania sprawozdania 23.04.2001

Cel wykonywania ćwiczenia:

Celem ćwiczenia jest porównanie rozkładów naprężeń uzyskanych na podstawie wzorów elementarnych z rozkładami uzyskanymi w wyniku pomiarów w przekroju cienkiej tarczy z niesymetrycznym wycięciem w postaci półkola o promieniu r.

Stanowisko pomiarowe:

- tarcza osłabiona karbem (1)

- zespół tensometrów oporowych (2)

- układ realizujący obciążenia (3)

- wartość zadawanej siły mierzona jest przy pomocy dynamometru (4)

- wielokanałowy wzmacniacz tensometryczny i rejestrator (5)

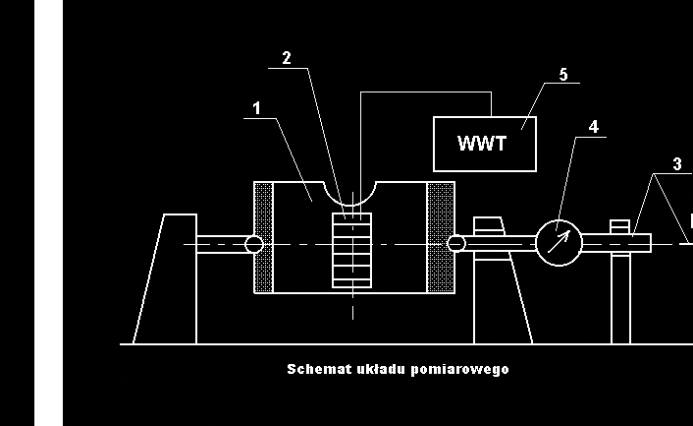
Badaniu została poddana prostokątna tarcza obciążona siłami rozciągającymi: P= 0, 20, 40, 60, 80 , 100, 120 ,140 , 160 [kG], przyłożonymi na dwóch przeciwległych brzegach. Aby uniknąć punktowego działania sił, obciążenie realizowane jest poprzez przynitowane wielopunktowo uchwyty tarcz. Stwarza to możliwość uzyskania równomiernego rozkładu naprężeń σ_x(y) w bliskiej odległości od obciążonych brzegów tarcz.

W przekroju tarczy osłabionym karbem zostały naklejone tensometry oporowe, które spełniają rolę przetworników pomiaro­wych i wraz ze wzmacniaczem tensometrycznym umożliwiają pomiar odkształcenia względnego, jakiemu ule­ga tarcza poddana obciążeniu.

Wchodzący w skład stanowiska wzmacniacz tensometryczny działa na zasa­dzie mostka zrównoważonego tj. po każdorazowej zmianie rezystancji tensometrów w celu dokonania odczytów należy układ skompensować, tak aby przyrząd pomiarowy wskazał ponownie stan równowagi.

Wstęp teoretyczny:

Karbem nazywamy takie fragmenty ciał (elementów maszyn), jak skoki przekroju, otwory itp., w których siły skupione wywołują lokalny wzrost naprężeń (spiętrzenie) , tym gwałtowniejszy im bardziej raptowna jest zmiana jego wymiarów poprzecznych.

Maksymalne naprężenia spowodowane istnieniem karbu są kilkakrotnie większe niż tak zwane naprężenia nominalne (obliczone w danym przekroju, tak jak gdyby karbu nie było).W naszym ćwiczeniu badaliśmy rozkład naprężeń w przekroju niebezpiecznym. W takich wypadkach mamy do czynienia z nierównomiernym, nieliniowym oraz dwuwymiarowym rozkładem naprężeń. Powodem tego stanu jest fakt, że włókna podłużne tarczy przecięte półkolem nie mogą przenosić sił wzdłużnych tuż przy granicy karbu i siły te są `przejmowane' przez najbliższe włókna nie przecięte.

Rozkład naprężeń w kierunku osi x1w takiej właśnie płytce.

Środek C, najbardziej osłabionego przekroju tarczy jest przesunięty względem przekroju pełnego o wielkość e, jak to zaznaczono na rysunku. Jeśli myślowo przetniemy tarczę w miejscu najbardziej osłabionym, to wysiłek przekroju będzie stanowić siła P i moment zginający Mg = Pe, zapewniające stan równowagi jednej części tarczy. Naprężenia nominalne w dowolnym punkcie przekroju 1-1 na odcinku A-K będą superpozycją naprężeń spowodowanych rozciąganiem oraz naprężeń spowodowanych zginaniem.

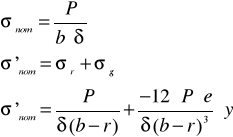
(1)

W zależności od wartości mimośrodu e mogą się pojawić na pewnej części odcinka A-K naprężenia ściskające σ₀^'<0.

Współczynnik spiętrzenia naprężeń dla takiego przykładu można zdefiniować w następującej postaci:

α^'_k=σ_k/σ^'_0k (2)

Wartość σ_k wyznaczamy na podstawie pomiarów tensometrycznych w pobliżu punktu K; natomiast σ^'_0k obliczamy za pomocą wzoru 1, podstawiając wartość współrzędnej y w punkcie K. Na wartości współczynnika tego mają wpływ również wymiary tarczy, takie jak promień wycięcia, szerokość tarczy oraz głębokość wycięcia.

Przebieg ćwiczenia:

* Obliczenie naprężeń nominalnych σ₀ , σ₀^'.

Siła [kG]	P1=20	P2=40	P3=60	P4=80	P5=100	P6=120	P7=140	P­8=160
σnom[MPa]	1.25	2.5	3,75	5	6,25	7,5	8,75	10

Tensometry są kolejno oddalone od brzegu półokręgu : 5,20,35,50,65,80;

Po odpowiednim uwzględnieniu punktu C Tensometr 3 znajduje się dokładnie w tym punkcie.

Tabela wyników obliczeniowych.

Nr kanału	Odległość y [mm]		P = 20 [kG]	P = 40 [kG]	P = 60 [kG]
			Naprężenia nominalne σo^'dla każdego kanału [MPa]
1	45		5,24	10,48	15,72
2	30		4,16	8,32	12,48
3	15		3,08	6,16	9,24
4	0		2	4	6
5	-15		0,92	1,84	2,76
6	-30		-0,16	-0,32	-0,48
Nr kanału	Odległość y [mm]		P = 80 [kG]	P = 100 [kG]	P = 120 [kG]
			Naprężenia nominalne σo^'dla każdego kanału [MPa]
1	45		20,96	26,20	31,44
2	30		16,64	20,8	24,96
3	15		12,32	15,4	18,48
4	0		8	10	12
5	-15		3,68	4,6	5,52
6	-30		-0,64	-0,8	-0,96
Nr kanału		Odległość y [mm]	P = 140 [kG]	P = 160 [kG]
			Naprężenia nominalne σo^'dla każdego kanału [MPa]
1		45	36,68	41,92
2		30	29,12	33,28
3		15	21,56	24,64
4		0	14	16
5		-15	6,44	7,36
6		-30	-1,12	-1,28

* Wyniki pomiarów wskazań tensometru dla wzrastającego obciążenia.;

Tabela wyników przeprowadzonych na zajęciach.

Wymiary tarczy: b = 160; δ = 1; r = 60;						Stała tensometru: k = 2,15 Moduł Younga: E = 2,1*10^5 [MPa]
Nr Kanału	Di (y)	ε0i	Wartość siły P [kG] 1[Pa] = [N/m^2] σxi =σxi*10^4 [MPa] 1[kG] = 10[N]
			P = 20				P = 40			P = 60
			εxi	εxi -ε0i	σxi		εxi	εxi -ε0i	σxi	εxi	εxi -ε0i	σxi
1	45	14,15	14,2	0,05	10,5		14,22	0,07	14,7	14,25	0,1	21
2	30	14,85	14,87	0,02	4,2		14,88	0,03	6,3	14,9	0,05	10,5
3	15	13,80	13,82	0,02	4,2		13,82	0,02	4,2	13,83	0,03	6,3
4	0	13,805	13,82	0,015	3,15		13,825	0,02	4,2	13,83	0,025	5,25
5	-15	14,45	14,55	0,1	2,1		14,56	0,11	2,31	14,57	0,12	2,52
6	-30	13,93	13,935	0,005	1,05		13,935	0,005	1,05	13,935	0,005	1,05

Wymiary tarczy: b = 160; δ = 1; r = 60;						Stała tensometru: k = 2,15 Moduł Younga: E = 2,1*10^5 [MPa]
Nr Kanału	Di (y)	ε0i	Wartość siły P [kG] 1[Pa] = [N/m^2] σxi =σxi*10^4 [MPa] 1[kG] = 10[N]
			P = 80				P = 100			P = 120
			εxi	εxi -ε0i	σxi		εxi	εxi -ε0i	σxi	εxi	εxi -ε0i	σxi
1	45	14,15	14,27	0,12	25,2		14,3	0,15	31,5	14,32	0,17	35,7
2	30	14,85	14,91	0,06	12,6		14,92	0,07	14,7	14,94	0,09	18,9
3	15	13,80	13,835	0,035	7,35		13,845	0,045	9,45	13,855	0,055	11,55
4	0	13,805	13,83	0,025	5,25		13,835	0,03	6,3	13,84	0,035	7,35
5	-15	14,45	14,6	0,15	3,15		14,61	0,16	3,36	14,612	0,162	3,402
6	-30	13,93	13,93	0	0		13,93	0	0	13,929	-0,001	-0,21

Wymiary tarczy: b = 160; δ = 1; r = 60;						Stała tensometru: k = 2,15 Moduł Younga: E = 2,1*10^5 [MPa]
Nr Kanału	Di (y)	ε0i	Wartość siły P [kG] 1[Pa] = [N/m^2] σxi =σxi*10^4 [MPa] 1[kG] = 10[N]
			P = 140				P = 160
			εxi	εxi -ε0i	σxi		εxi	εxi -ε0i	σxi
1	45	14,15	14,35	0,2	42		14,38	0,23	48,3
2	30	14,85	14,95	0,1	21		14,97	0,12	25,2
3	15	13,80	13,86	0,06	12,6		13,87	0,07	14,7
4	0	13,805	13,845	0,04	8,4		13,855	0,05	10,5
5	-15	14,45	14,65	0,2	4,2		14,67	0,22	4,62
6	-30	13,93	13,926	-0,004	-0,84		13,929	-0,001	-0,21

Obliczenie współczynnika spiętrzenia naprężeń α^'_k w otoczeniu punktu K.

Dla siły P = 200 N	Dla siły P = 400 N	Dla siły P. = 600 N	Dla siły P. = 800 N	Dla siły P. = 1000 N	Dla siły P. = 1200 N	Dla siły P. = 1400 N	Dla siły P. = 1600 N
α^'k = 0,2	α^'k = 0,140	α^'k = 0,133	α^'k = 0,120	α^'k = 0,120	α^'k = 0,113	α^'k = 0,114	α^'k = 0,115

* Wyniki pomiarów wskazań tensometru przy malejącym obciążeniu.

Wymiary tarczy: b = 160; δ = 1; r = 60;						Stała tensometru: k = 2,15 Moduł Younga: E = 2,1*10^5 [MPa]
Nr Kanału	Di (y)	ε0i	Wartość siły P [kG] 1[Pa] = [N/m^2] σxi =σxi*10^4 [MPa] 1[kG] = 10[N]
			P = 160				P = 140			P = 120
			εxi	εxi -ε0i	σxi		εxi	εxi -ε0i	σxi	εxi	εxi -ε0i	σxi
1	45	14,16	14,38	0,22	46,2		14,36	0,2	42	14,34	0,18	37,8
2	30	14,85	14,97	0,12	25,2		14,96	0,11	23,1	14,95	0,1	21
3	15	13,8	13,87	0,07	14,7		13,87	0,07	14,7	13,86	0,06	12,6
4	0	13,81	13,855	0,045	9,45		13,85	0,04	8,4	13,845	0,035	7,35
5	-15	14,64	14,67	0,03	6,3		14,65	0,01	2,1	14,665	0,025	5,25
6	-30	13,94	13,929	-0,011	-2,31		13,929	-0,011	-2,31	13,929	-0,011	-2,31

Wymiary tarczy: b = 160; δ = 1; r = 60;						Stała tensometru: k = 2,15 Moduł Younga: E = 2,1*10^5 [MPa]
Nr Kanału	Di (y)	ε0i	Wartość siły P [kG] 1[Pa] = [N/m^2] σxi =σxi*10^4 [MPa] 1[kG] = 10[N]
			P = 100				P = 80			P = 60
			εxi	εxi -ε0i	σxi		εxi	εxi -ε0i	σxi	εxi	εxi -ε0i	σxi
1	45	14,16	14,31	0,15	31,5		14,28	0,12	25,2	14,26	0,1	21
2	30	14,85	14,94	0,09	18,9		14,92	0,07	14,7	14,9	0,05	10,5
3	15	13,8	13,85	0,05	10,5		13,84	0,04	8,4	13,83	0,03	6,3
4	0	13,81	13,837	0,027	5,67		13,831	0,021	4,41	13,827	0,017	3,57
5	-15	14,64	14,661	0,021	4,41		14,66	0,02	4,2	14,66	0,02	4,2
6	-30	13,94	13,93	-0,01	-2,1		13,931	-0,009	-1,89	13,932	-0,008	-1,68

Wymiary tarczy: b = 160; δ = 1; r = 60;						Stała tensometru: k = 2,15 Moduł Younga: E = 2,1*10^5 [MPa]
Nr Kanału	Di (y)	ε0i	Wartość siły P [kG] 1[Pa] = [N/m^2] σxi =σxi*10^4 [MPa] 1[kG] = 10[N]
			P = 40				P = 20
			εxi	εxi -ε0i	σxi		εxi	εxi -ε0i	σxi
1	45	14,16	14,23	0,07	14,7		14,2	0,04	8,4
2	30	14,85	14,89	0,04	8,4		14,88	0,03	6,3
3	15	13,8	13,825	0,025	5,25		13,82	0,02	4,2
4	0	13,81	13,825	0,015	3,15		13,82	0,01	2,1
5	-15	14,64	14,66	0,02	4,2		14,66	0,02	4,2
6	-30	13,94	13,935	-0,005	-1,05		13,94	0	0

Wykresy rozkładu naprężeń dla poszczególnych sił:

Wnioski:

Przeprowadzone przeze mnie pomiary potwierdziły występujące zjawisko karbu w badanej próbce . Naprężenie nominalne występujące w przekroju osłabionym otworem znacznie przekraczały nominalne dla normalnych wymiarów próbki . Przeprowadzone pomiary odkształceń próbki pod wpływem siły pozwoliły na obliczenie rzeczywistych naprężeń występujących w przekroju , gdzie występuje karb . Przewyższają one

obliczone empirycznie naprężenia nominalne około 5 razy .

Otrzymane wyniki pokazują jak niebezpieczne i ważne jest w praktyce zjawisko karbu .

Występujące w tym miejscu naprężenia mogą powodować zniszczenie konstrukcji , dlatego w praktyce

należy unikać takiego zjawiska . Uniknięcie karbu można zrealizować za pomocą odpowiedniego

zaprojektowania przejść na granicy występowania największych naprężeń np.: gwałtowne skoki średnic

zastępować stożkiem

---