POLITECHNIKA POZNAŃSKA INSTYTUT AUTOMATYKI I INŻYNIERII INFORMATYCZNEJ Zakład Automatyki i Robotyki Laboratorium podstaw automatyki
		Ćwiczenie nr 2 Temat: Charakterystyki częstotliwościowe układów liniowych.
Rok akad. 2007/2008	Paulina Jankowiak		Wykonanie ćwiczenia 13.10.2008r.	Oddanie sprawozdania 19.10.2008r.
Wydział Elektryczny
Studia stacjonarne
Elektrotechnika
						Ocena:
Grupa E3
UWAGI:

1. Cel ćwiczenia

Ćwiczenie ma na celu zapoznanie się z charakterystykami częstotliwościowymi podstawowych

elementów automatyki, takimi jak: charakterystyka amplitudowo-fazowa, logarytmiczna

charakterystyka modułu oraz logarytmiczna charakterystyka fazowa, z jednoczesną analizą

wpływu poszczególnych parametrów na ich kształt.

2. Podstawowe wiadomości

Zawarte w skrypcie

3. Przebieg ćwiczenia

3.1 Wpływ wartości parametrów na charakterystyki częstotliwościowe.

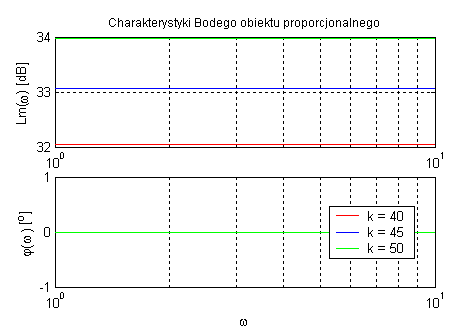
Obiekt proporcjonalny (zmienne k).

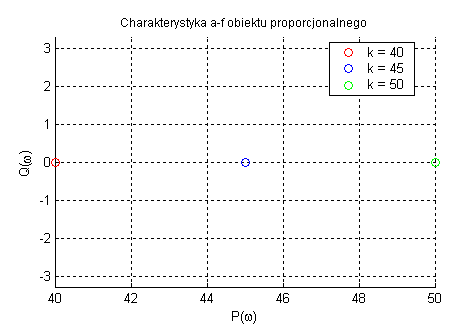
Obiekt proporcjonalny ma jedynie wzmocnić amplitudę sygnału, bez zmiany jego fazy. Z tego powodu wzrost parametru k ma wpływ tylko na podniesienie charakterystyki amplitudowej lub przesunięcie w prawo punktu dla charakterystyki amplitudowo-fazowej.

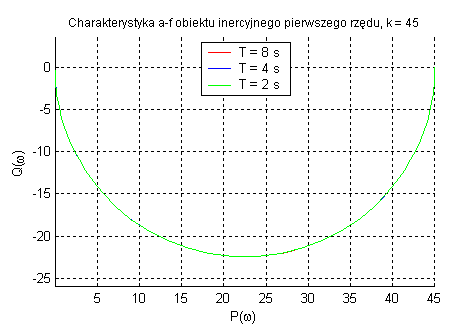
Obiekt inercyjny pierwszego rzędu

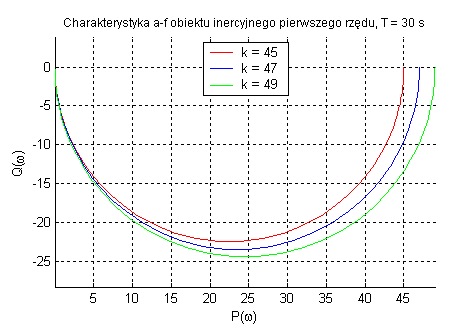
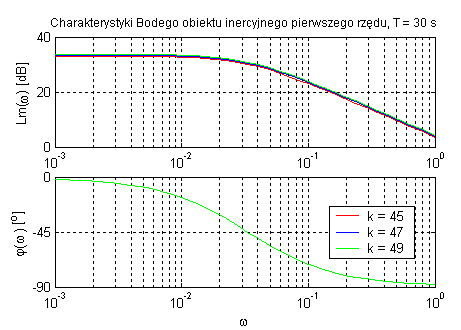
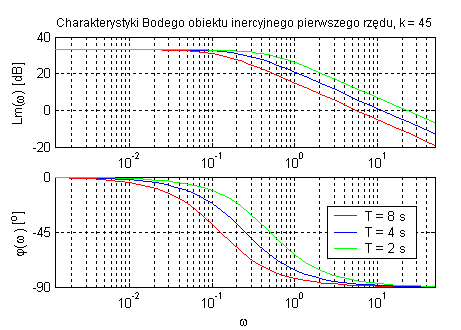
Element inercyjny wprowadza zmiany zarówno w module jak i fazie sygnału. Parametr k decyduje o amplitudzie ale nie ma wpływu na na zmianę fazy. Charakterystycznym punktem jest ω=1/T, dla którego przesunięcie fazowe jest równe -45˚. Stała czasowa T ma wpływ na szerokość pasma przenoszenia obiektu. Pasmo przenoszenia zmniejsza się wraz ze wzrostem T.

Obiekt dwuinercyjny (zmienne k oraz T₁).

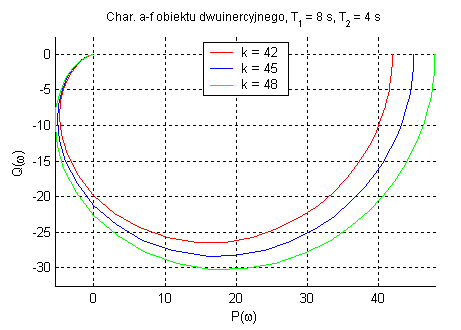
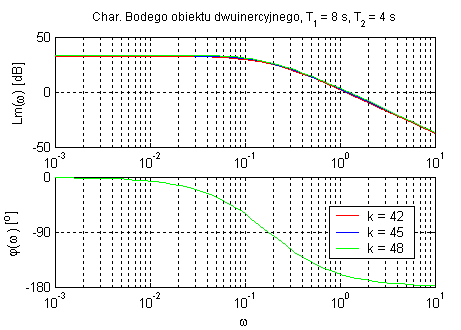
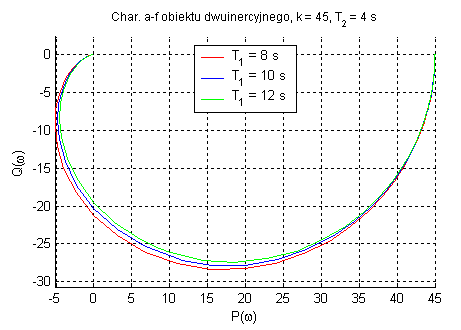
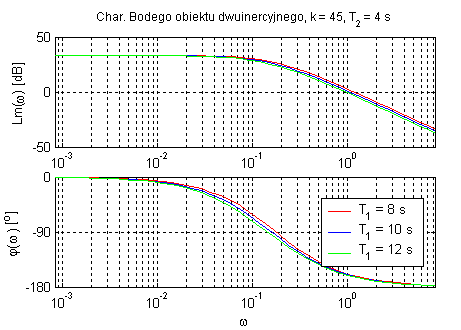
Dodatkowy człon inercyjny zwiększa opóźnienie układu(do 180°). Podobnie jak w obiekcie

inercyjnym pierwszego rzędu parametr k wpływa tylko na amplitudę. T1 okresla dla jakiej częstotliwości następuje tłumienie sygnału. Charakterystyka Nyquista obejmuje dwie ćwiartki układu zmiennej zespolonej.

Obiekt inercyjny n-tego rzędu (zmienne k, T oraz n).

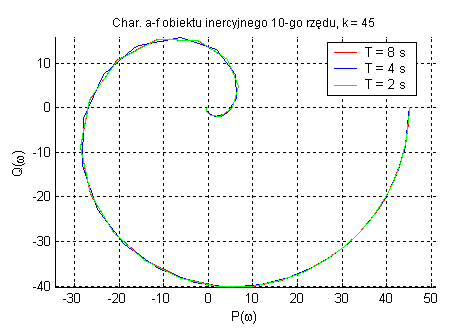
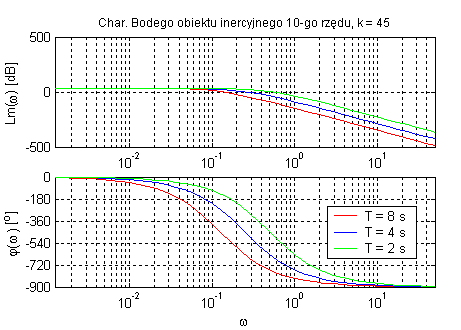
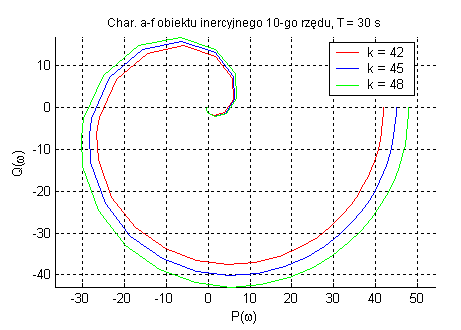
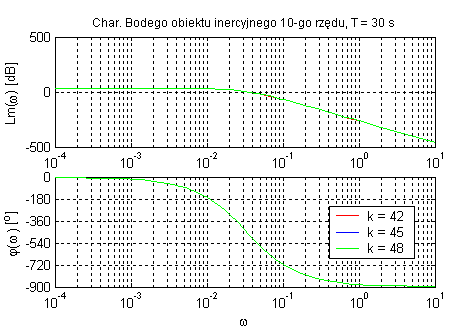
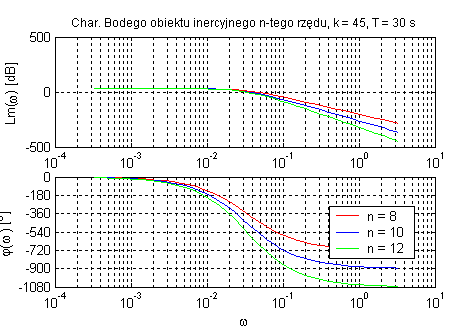
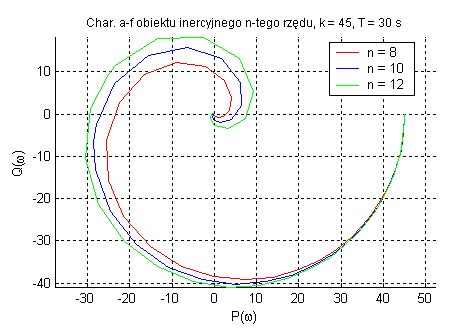
Zwiększenie rzędu inercji zwiększa podatność zmiany fazy i modułu ze względu na zmianę pulsacji. Opóźnienie fazowe wynosi n•90˚. Parametr k wpływa tylko na amplitudę oraz T określa ω_g , a rząd inercji obiektu decyduje o nachyleniu charakterystyki fazowej.

Obiekt oscylacyjny (przy k=1, zmienne ω_n oraz ξ).

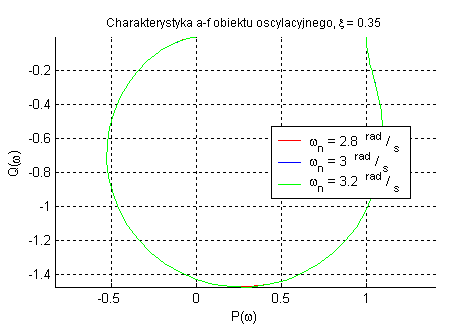
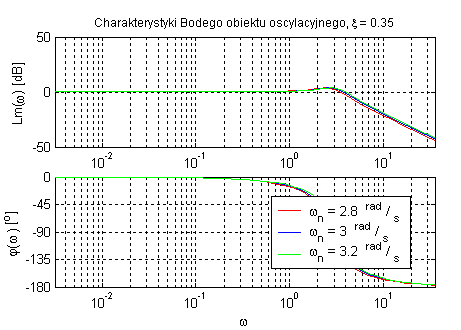
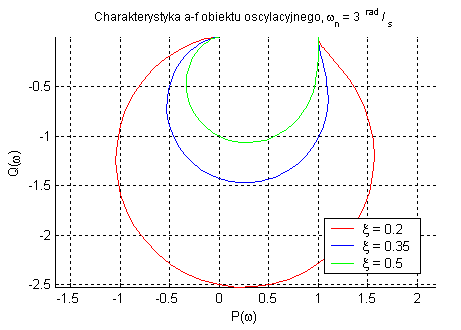
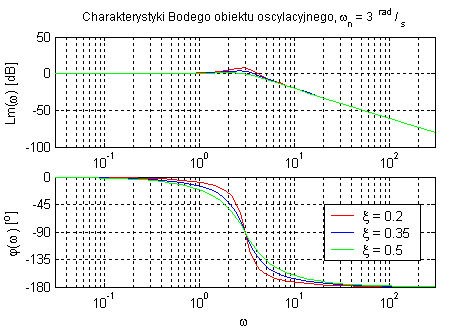
Obiekt ten ma tendencję do oscylacji w zależności od parametru tłumienia ξ. Parametr ω_n decyduje o pulsacji, w której następuje tłumienie sygnału, zwiększenie przesunięcia fazowego oraz zakrzywianie charakterystyk.

Obiekt całkujący idealny (zmienne k).

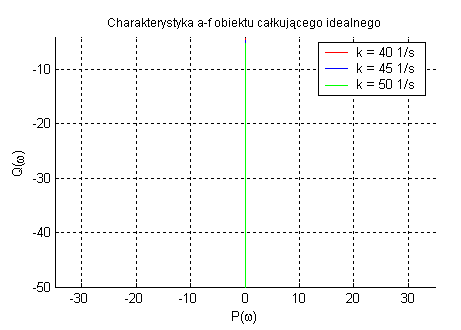
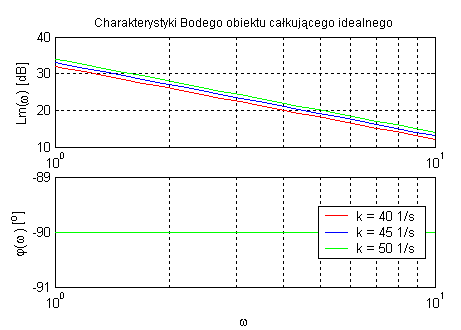
Element całkujący idealny zmniejsza amplitudę sygnału proporcjonalnie do pulsacji oraz przesuwa fazę sygnału o -90˚.

Obiekt całkujący z inercją (zmienne k oraz T).

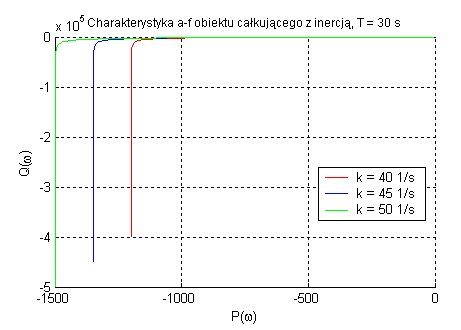
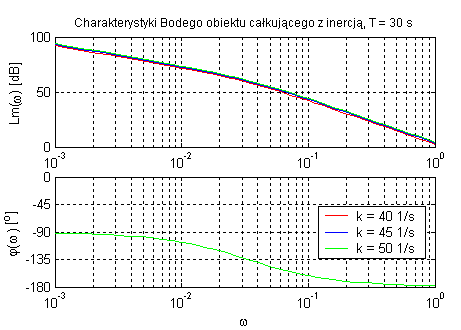
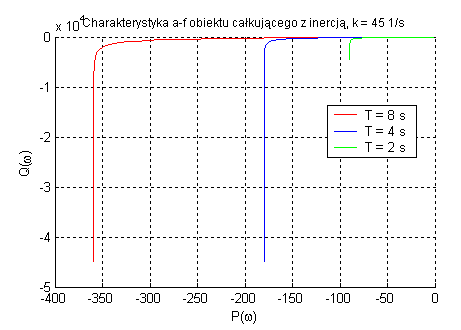
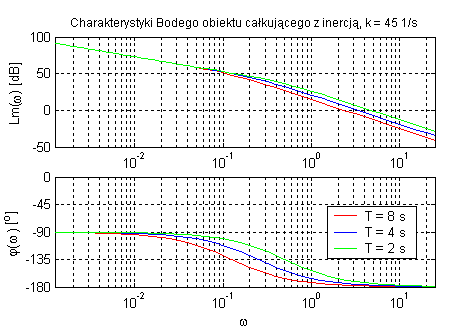
Obiekt całkujący rzeczywisty oraz obiekt całkujący idealny różnią się tym że ten pierwszy uwzględnia jego bezwładność. Moment przegięcia charakterystyk zależy od parametru T, a dodanie inercji powoduje zwiększenie się opóźnienia fazowego (do 180˚). Regulacja wzmocnienia obiektu wpływa na wartość amplitudy.

Obiekt różniczkujący rzeczywisty (zmienne k oraz T).

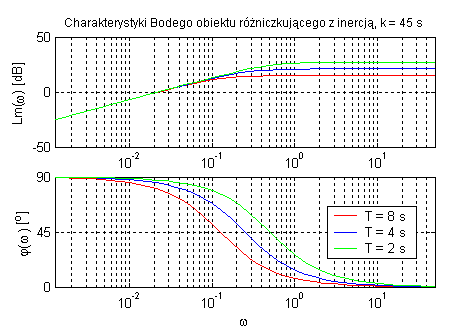
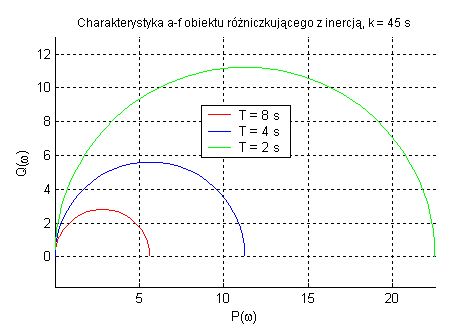
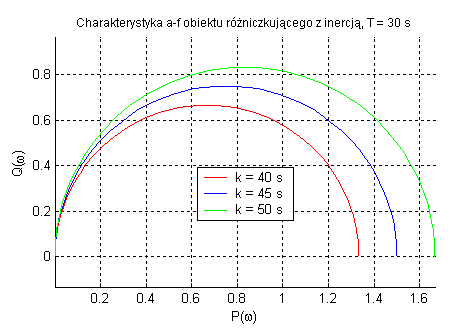
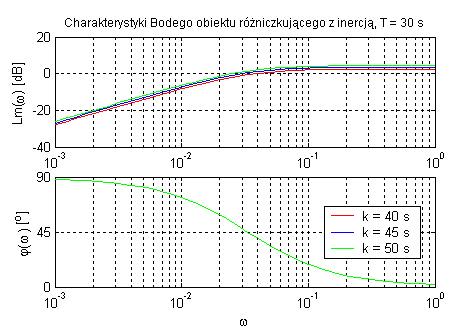
W obiekcie różniczkującym sygnał wyjściowy zależy od szybkości zmian sygnału wejściowego. Parametr k powoduje zmianę amplitudy ale nie ma wpływu na przesunięcie fazowe. Natomiast T określa pulsację.

Obiekt inercyjny pierwszego rzędu z opóźnieniem transportowym (zmienne k, T oraz T₀).

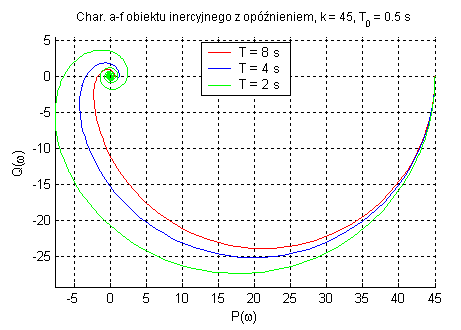
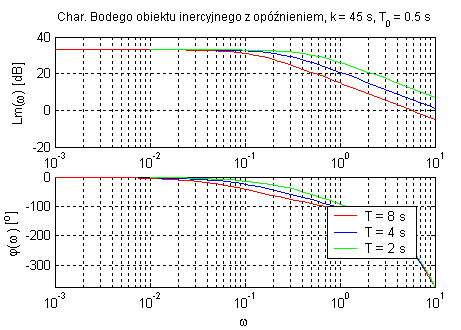
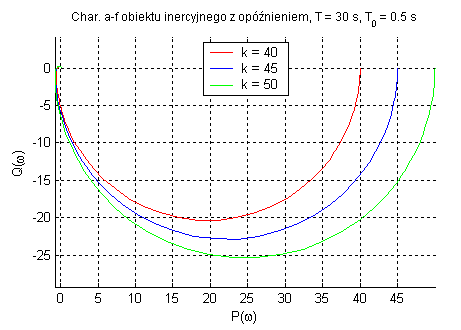
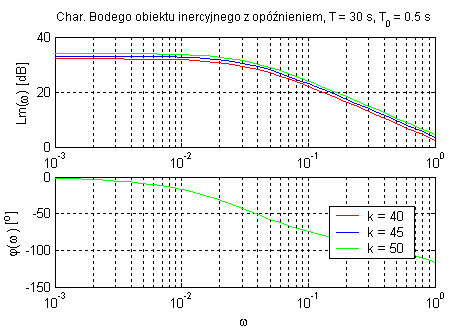
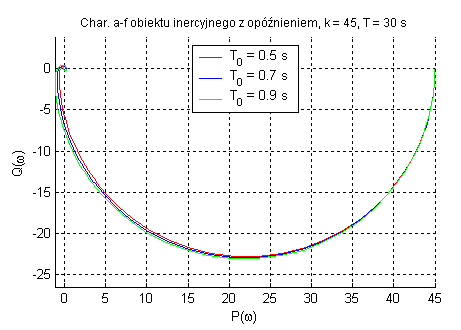
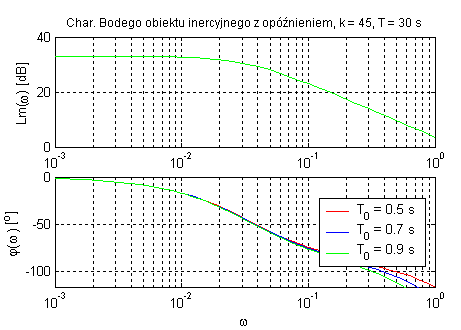
Zadaniem elementu opóźniającego jest opóźnienie sygnału w czasie. Parametr k wpływa tylko na amplitudę sygnału, a T określa punkt przegięcia charakterystyk.

3.2. Analityczne wyznaczenie odpowiedzi czasowej.

Wyznaczyć odpowiedź na wymuszenie harmoniczne u(t)=1.0sin(55.0t) obiektu różniczkującego rzeczywistego o transmitancji podanej poniżej i parametrach k=45.0 T=30.0s.

Ponieważ
dlatego
a

więc

( e zostało zapisane w ten sposób z powodu problemów z zapisaniem „-” w potędze.

3.3. Analityczne wyznaczenie wykresów Bodego.

Poniżej przedstawiono charakterystyki Bodego zadanego obiektu.

6

---