Ćw. 27 Pomiar przewodności cieplnej metali

1. Wstęp teoretyczny

Pomiędzy ciałami ogrzanymi do różnych temperatur zachodzi wymiana ciepła, czyli transport energii. Ciało o wyższej temperaturze traci ciepło, a ciało o niższej temperaturze je zyskuje. Wymiana ta trwa tak długo, dopóki temperatury obu ciał nie zrównają się. Znamy trzy sposoby wymiany (przenoszenia) ciepła:

a) przez prądy konwekcyjne (unoszenie ciepła),

b) przez promieniowanie,

c) przez przewodzenie.

Przewodnictwo cieplne polega na przekazywaniu energii pomiędzy częściami ciała, których temperatury są różne. Z tym zjawiskiem mamy do czynienia wówczas, gdy wydzieloną część ciała podgrzejemy. Po pewnym czasie dzięki przekazywaniu energii, temperatura całego ciała wyrówna się. Wielkością przenoszoną jest energia wewnętrzna ciała, a zjawisko zachodzi dzięki temu, że w tym ciele występuje gradient temperatury.

Współczynnik przewodnictwa ciepła, (k lub λ), określa zdolność substancji do przewodzenia ciepła. W tych samych warunkach więcej ciepła przepłynie przez substancję o większym współczynniku przewodności cieplnej.

, dla duraluminium wynosi= 160,5 W/m×K

Ciepło właściwe - energia podnosząca temperaturę ciała o jednostkowej masie o jednostkę temperatury.

, które dla duraluminium wynosi 880 J/(kg*K)3. Przebieg ćwiczenia

Różnica temperatur między końcami pręta w zależności od czasu:

20,1	1420
20,2	1440
20,3	1460
20,3	1480
20,4	1500
20,4	1520
20,5	1540
20,5	1560
20,6	1580
20,6	1600
20,7	1620
20,7	1640
20,8	1660
20,8	1680
20,9	1700
20,9	1720
20,9	1740
21	1760
21	1780
21,1	1800
21,1	1820
21,1	1840
21,2	1860
21,2	1880
21,3	1900
21,3	1920
21,3	1940
21,4	1960
21,4	1980
21,4	2000
21,5	2020
21,5	2040
21,5	2060
21,6	2080
21,6	2100

ΔT[ ̊ C]	t[s]
6	0
6,4	15
6,8	30
7,1	45
7,4	60
7,8	75
8,2	90
8,6	105
8,9	120
9,3	135
9,6	150
9,9	165
10,2	180
10,5	200
10,8	220
11	240
11,3	260
11,5	280
11,9	300
12,2	320
12,5	340
12,8	360
13	380
13,3	400
13,6	420
13,9	440
14,1	460
14,3	480
14,6	500
14,8	520
15	540
15,2	560
15,4	580
15,6	600
15,8	620
16	640
16,2	660
16,3	680
16,5	700
16,7	720
16,8	740
17	760
17,1	780
17,2	800
17,4	820
17,5	840
17,6	860
17,8	880
17,9	900
18	920
18,1	940
18,2	960
18,3	980
18,5	1000
18,6	1020
18,7	1040
18,8	1060
18,9	1080
18,9	1100
19	1120
19,1	1140
19,2	1160
19,3	1180
19,4	1200
19,5	1220
19,5	1240
19,6	1260
19,7	1280
19,7	1300
19,8	1320
19,9	1340
20	1360
20	1380
20,1	1400
21,6	2120
21,7	2140
21,7	2160
21,7	2180
21,8	2200
21,8	2220
21,8	2240
21,8	2260
21,9	2280
21,9	2300
21,9	2320
21,9	2340
22	2360
22,1	2380
22,1	2400
22,1	2420
22,1	2440
22,2	2460
22,2	2480
22,2	2500
22,2	2520
22,3	2540
22,3	2560
22,3	2580
22,3	2600
22,4	2620
22,4	2640
22,4	2660
22,4	2680
22,4	2700
22,4	2720
22,5	2740
22,5	2760
22,5	2780
22,5	2800
22,5	2820

22,5	2840
22,6	2860
22,6	2880
22,6	2900
22,6	2920
22,7	2940
22,7	2960
22,7	2980
22,7	3000
22,7	3020
22,7	3040
22,8	3060
22,8	3080
22,8	3100
22,8	3120
22,8	3140
22,8	3160
22,9	3180
22,9	3200
22,9	3220
22,9	3240
23	3260
23	3280
23	3300
23	3320
23	3340
23	3360
23,1	3380

Długość pręta duraluminiowego:

l₁ = 260,05mm

l₂ = 260,09mm

l₃ = 260,10mm

Wartość średnia: l_śr = 260,08mm

Promień pręta:

2R₁ = 19,00mm

2R₂ = 18,62mm

2R₃ = 18,32mm

R₁ = 9,5mm

R₂ = 9,31mm

R₃ = 9,16mm

Wartość średnia: R_śr = 9,32mm

U = 7,5V

I = 5,8A

masa pręta: 196,7g4. Opracowanie wyników pomiaru

Równanie prostej aproksymacyjnej: y = -0,001x-0,441

gdy y = -1, x= 559s - cieplna stała czasowa

Obliczenie współczynnika przewodnictwa cieplnego K za pomocą wzoru:

gdzie:

P = U ∙ I

U = 7,5 V

I = 5,8 A

l - długość pręta = 260,08*10^-3 m

S = π R²

R = 9,32*10^-3 m

ΔT = 23,5 ̊ C = 296,5K

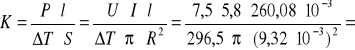
139,83 W/mK

ΔU = ±0,1V

ΔI = ±0,1A

Δl - ±0,01m

ΔR = ±0,02m

Niepewność z pochodnej cząstkowej:

ΔK = ±0,71 W/mK

(ΔK/K)*100% = 0,51%

Obliczenie ciepła właściwego badanego materiału korzystając z następującego wzoru:

gdzie:

ρ - gęstość materiału pręta obliczona ze wzoru ρ=m/V = 2770,4 kg/m³

m - masa próbki = 196,7g

V - objętość pręta = π*R^2*l =7,10*10^-5 m³

τ_c - „cieplna” stała czasowa = 559s

Δm = ±1g

Δ τ_c = ± 0,02s

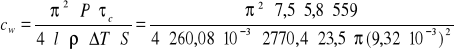
= 929,16 J/(kg*K)

Δc_w = 0,58 J/(kg*K)

5. Wyniki końcowe

K = (139,83±0,71) W/mK

c_w = (929,16±0,58) J/(kg*K)6. Wnioski

Na podstawie pomiarów różnic temperatury na końcach pręta oraz masy, średnicy i długości pręta wyznaczony został współczynnik przewodnictwa cieplnego, jak i ciepło właściwe duraluminium. Porównując wartości wyznaczone doświadczalnie z wartościami stabelaryzowanymi dostrzegam pewne odstępstwa:

dla współczynnika przewodnictwa cieplnego różnica wynosi: 20,67 W/(mK)

dla ciepła właściwego różnica wynosi: 49,15 J/(kg/K)

---