Budowa modelu ekonometrycznego
Badam kształtowanie się liczby ludności w Polsce na przestrzeni lat 1980-2001i wpływające na tę liczbę czynniki. Określę w jakim stopniu dany czynnik wpływał na tę liczbę oraz który miał na nią największy wpływ. Zmienną objaśnianą y w tym modelu jest liczba ludności przedstawiona w milionach, a czynnikami na nią przypuszczalnie wpływającymi, czyli zmiennymi objaśniającymi są: X1-ludność w miastach w %, X2- urodzenia żywe w tyś., X3- liczba zgonów, X4- przyrost naturalny na 1000mieszkańców, X5-długość życia kobiet w latach, X6-długość życia mężczyzn w latach, X7-spożycie mięsa w kg./osobę, X8-samochody na tyś.mieszkańców.
y-ludność w mln |
|
|
|
X1-ludność w miastach w % |
|
|
|
X2- urodzenia żywe w tys. |
|
|
|
X3- zgony w tys. |
|
|
|
X4- przyrost naturalny na 1000mieszkańców |
|||
X5-długość życia kobiet w latach |
|
||
X6-długość życia męż. W latach |
|
||
X7-spożycie mięsa w kg./osobę |
|
||
X8-samochody na tys.mieszkańców |
|
||
Dane w tabeli pochodzą z rocznika statystycznego 2002 roku.
lata |
Y |
X1 |
X2 |
X3 |
X4 |
X5 |
X6 |
X7 |
X8 |
1980 |
35,735 |
58,7 |
692,8 |
350,2 |
9,6 |
75,4 |
66,9 |
74 |
67 |
1990 |
38,183 |
61,8 |
545,8 |
388,4 |
4,1 |
75,3 |
66,3 |
68,6 |
138 |
1995 |
38,609 |
61,8 |
433,1 |
386,1 |
1,2 |
76,4 |
67,6 |
63,4 |
195 |
1997 |
38,65 |
61,9 |
412,7 |
380,2 |
0,9 |
77 |
68,5 |
61,7 |
221 |
1998 |
38,666 |
61,9 |
395,6 |
375,3 |
0,5 |
77,3 |
68,9 |
64,7 |
230 |
1999 |
38,654 |
61,9 |
382 |
381,4 |
0,02 |
77,5 |
68,8 |
66,8 |
240 |
2000 |
38,644 |
61,8 |
378,3 |
368 |
0,3 |
78 |
69,7 |
65,4 |
259 |
2001 |
38,632 |
61,7 |
368,2 |
363,2 |
0,1 |
78,4 |
70,2 |
66,7 |
272 |
średnia arytmetyczna |
38,22163 |
61,4375 |
451,0625 |
374,1 |
2,09 |
76,9125 |
68,3625 |
66,4125 |
202,75 |
odchylenie standardowe |
1,017671 |
1,108329 |
112,8924 |
12,91544 |
3,308552 |
1,13696 |
1,343702 |
3,738387 |
68,76824 |
współczynnik zmienności |
0,026626 |
0,01804 |
0,250281 |
0,034524 |
1,583039 |
0,014783 |
0,019656 |
0,05629 |
0,339178 |
1,8% 25% 3,4% 158% 1,48% 1,96% 5,6% 33,9%
![]()
=![]()
![]()
Sx =![]()
Vx = ![]()
Przeprowadzam weryfikacje zmiennych objaśniających na podstawie wyliczonego współczynnika zmienności. Z modelu usuwam zmienne, dla których współczynnik zmienności wynosi mniej niż 10%.
Po usunięciu nieistotnych zmiennych model przyjął zaprezentowaną niżej postać.
y-ludność w mln |
|
|
|
X1- urodzenia żywe w tys. |
|
|
|
X2- przyrost naturalny na 1000 mieszkańców |
|||
X3- samochody na tys. mieszkańców |
|
||
lata |
Y |
X1 |
X2 |
X3 |
1980 |
35,735 |
692,8 |
9,6 |
67 |
1990 |
38,183 |
545,8 |
4,1 |
138 |
1995 |
38,609 |
433,1 |
1,2 |
195 |
1997 |
38,65 |
412,7 |
0,9 |
221 |
1998 |
38,666 |
395,6 |
0,5 |
230 |
1999 |
38,654 |
382 |
0,02 |
240 |
2000 |
38,644 |
378,3 |
0,3 |
259 |
2001 |
38,632 |
368,2 |
0,1 |
272 |
średnia arytmetyczna |
38,22163 |
451,0625 |
2,09 |
202,75 |
odch. stan. |
1,017671 |
112,8924 |
3,308552 |
68,76824 |
wsp.zmienn. |
0,026626 |
0,250281 |
1,583039 |
0,339178 |
Ustalam współczynnik korelacji (zależności) między objaśnianą a poszczególnymi objaśniającymi oraz miedzy poszczególnymi objaśniającymi za pomocą wzoru:
rxy=![]()
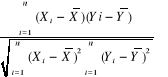
X1- |
(X1- |
X2- |
(X2- |
X3- |
(X3- |
Y- |
(Y- |
|
241,8 |
58467,24 |
7,51 |
56,4001 |
-135,75 |
18428,06 |
-2,485 |
6,175225 |
|
94,8 |
8987,04 |
2,01 |
4,0401 |
-64,75 |
4192,563 |
-0,037 |
0,001369 |
|
-17,9 |
320,41 |
-0,89 |
0,7921 |
-7,75 |
60,0625 |
0,389 |
0,151321 |
|
-38,3 |
1466,89 |
-1,19 |
1,4161 |
18,25 |
333,0625 |
0,43 |
0,1849 |
|
-55,4 |
3069,16 |
-1,59 |
2,5281 |
27,25 |
742,5625 |
0,446 |
0,198916 |
|
-69 |
4761 |
-2,07 |
4,2849 |
37,25 |
1387,563 |
0,434 |
0,188356 |
|
-72,7 |
5285,29 |
-1,79 |
3,2041 |
56,25 |
3164,063 |
0,424 |
0,179776 |
|
-82,8 |
6855,84 |
-1,99 |
3,9601 |
69,25 |
4795,563 |
0,412 |
0,169744 |
|
|
89212,87 |
|
76,6256 |
|
33103,5 |
|
7,249607 |
SUMA |
(X1- |
(X2- |
(X3- |
-600,87 |
-18,6 |
337,3 |
-3,5 |
-0,074 |
2,4 |
-6,96 |
-0,35 |
-3 |
-16,47 |
-0,5 |
7,85 |
-24,7 |
-0,7 |
12,15 |
-29,9 |
-0,87 |
16,16 |
-30,8 |
-0,76 |
23,85 |
-34,1 |
-0,82 |
28,53 |
SUMA -747,51 -22,6 425,24
MACIERZ Ro |
-0,92937 |
YX1 |
|
|
|
-0,96656 |
YX2 |
|
|
0,868099 |
YX3 |
|
|
|
|
|
X1 |
X2 |
X3 |
X1 |
1 |
0,993091 |
-0,9886 |
X2 |
0,993091 |
1 |
-0,96786 |
X3 |
-0,9886 |
-0,96786 |
1 |
Ponieważ zmienne objaśniające są ze sobą silnie skorelowane prawdopodobnie wystarczy wziąć jedną z nich aby opisać zmienną objaśnianą. Najsilniej skorelowana ze zmienną objaśnianą jest zmienna X2, dla potwierdzania tego stosuję metodę Helwiga. Rozpatruje wszystkie kombinacje m-zmiennych ze zbioru X. Ich liczba wynosi: 2![]()
-1
Określam indywidualną pojemność informacyjną nośnika Xj wchodzącego w skład S-tej kombinacji: hsj =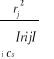
A następnie obliczamy integralną pojemność informacyjną S-tej kombinacji: Hs = ![]()
Możliwe kombinacje:
K1 {X1} |
K4 {X1, X2} |
|
|
|
|
|
|
K2 {X2} |
K5 {X1, X3} |
|
|
|
|
|
|
K3 {X3} |
K6 {X2, X3} |
|
|
|
|
|
|
|
K7 {X1,X2,X3} |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ro1 {-0,93} |
R1 [1] |
|
|
|
H1= |
0,8649 |
|
Ro2 {-0,97} |
R2 [1] |
|
|
|
H2= |
0,9409 |
|
Ro3 {0,87} |
R3 [1] |
|
|
|
H3= |
0,7569 |
|
Ro4 |
-0,93 |
R4 |
1 |
0,99 |
|
H4= |
0,9069 |
|
-0,97 |
|
0,99 |
1 |
|
|
|
|
|
|
|
|
|
|
|
Ro5 |
-0,93 |
R5 |
1 |
-0,98 |
|
H5= |
0,8206 |
|
0,87 |
|
-0,98 |
1 |
|
|
|
|
|
|
|
|
|
|
|
Ro6 |
-0,97 |
R6 |
1 |
-0,9565 |
|
H6= |
0,8673 |
|
0,87 |
|
-0,9565 |
1 |
|
|
|
|
|
|
|
|
|
|
|
Ro7 |
-0,93 |
R7 |
1 |
0,992053 |
-0,98311 |
|
|
|
-0,97 |
|
0,992053 |
1 |
-0,9565 |
|
|
|
0,87 |
|
-0,98311 |
-0,9565 |
1 |
H7= |
0.8668 |
|
|
|
|
|
|
|
|
Moje przypuszczenia się sprawdziły, metoda Helwiga wskazała na zmienną X2.
Obliczam klasyczną metodą najmniejszych kwadratów parametry strukturalne modelu.
Model, którego parametry szacuje ma postać: ỹ = a0 + a1 * X2
Zapis macierzowy modelu: ă = (X![]()
X)![]()
* (X![]()
Y)
Wyznaczam wektor Y obserwacji zmiennej objaśnianej oraz macierz X obserwacji zmiennej objaśniającej.
1 |
9,6 |
1 |
4,1 |
1 |
1,2 |
1 |
0,9 |
1 |
0,5 |
1 |
0,02 |
1 |
0,3 |
1 |
0,3 |
X=
35,735 |
38,183 |
38,609 |
38,65 |
38,666 |
38,654 |
38,644 |
38,632 |
Y=
Transponuje macierz X obserwacji zmiennej objaśniającej.
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
9,6 |
4,1 |
1,2 |
0,9 |
0,5 |
0,02 |
0,3 |
0,3 |
X![]()
=
Dążę do otrzymania macierzy odwrotnej iloczynu (X![]()
X).
X![]()
X = ![]()
Aby otrzymać macierz odwrotną posługuję się wzorem 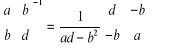
(X![]()
X)![]()
= ![]()
Wyliczam iloczyn macierzy X![]()
i Y
X![]()
Y = ![]()
Ze wzoru ă = (X![]()
X)![]()
* (X![]()
Y) wyliczam a0 i a1
a0 = 38,85
a1 = -0,3
Model, którego parametry szacuje ma postać: ỹ = 38,85 - 0,3X2
Przypuszczalnie wzrost przyrostu naturalnego o jedną osobę na 1000 mieszkańców, powoduje spadek liczby ludności o 300 tysięcy osób. Może być to spowodowane większą liczbą zgonów niż urodzeń.
Przeprowadzam weryfikacje wyników. ỹ=Xi*a1
Y |
X2 |
ỹ |
(Y- ỹ) |
(Y- |
35,735 |
9,6 |
35,97 |
0,055 |
6,175 |
38,183 |
4,1 |
37,62 |
0,314 |
0,002 |
38,609 |
1,2 |
38,49 |
0,014 |
0,152 |
38,65 |
0,9 |
38,58 |
0,005 |
0,185 |
38,666 |
0,5 |
38,7 |
0,001 |
0,202 |
38,654 |
0,02 |
38,84 |
0,036 |
0,185 |
38,644 |
0,3 |
38,76 |
0,014 |
0,176 |
38,632 |
0,1 |
38,82 |
0,036 |
0,168 |
|
|
|
|
|
Obliczam ile wynosi błąd standardowy modelu.
∑(Y- ỹ)![]()
S![]()
= ----------------- = 0,079
n-k
S=0,28
Błąd standardowy modelu dotyczący liczby ludności szacowany za pomocą modelu
ỹ = 38,85 - 0,3X2 wynosi 0,28
Obliczam ile procent zmiennej objaśnianej jest wyjaśnione zmienną objaśniającą.
∑(Y- ỹ)![]()
ϕ![]()
= ------------------------- =0,0655
∑(Y-![]()
)![]()
R![]()
=1-ϕ![]()
R![]()
= 0,9345
Zmienność liczby ludności jest wyjaśniona przez przyrost naturalny w 93,45%.
W celu sprawdzenia istotności parametru przeprowadzam test Fishera.
Hipoteza pierwsza:
Ho; a2=0 przyrost naturalny nie ma wpływu na liczbę ludności
Hipoteza druga:
H1; a2≠0 przyrost naturalny ma wpływ na liczbę ludności
F=![]()
* ![]()
F= 12,23
F*= 5,987 wartość krytyczna rozkładu F, odczytana z tablic Fishera przy poziomie istotności a 0,05 k-1 n-k stopnia swobody
F>F* odrzucam hipotezę pierwszą, hipoteza pierwsza jest prawdziwa
Praca pochodzi z serwisu www.e-sciagi.pl
Wyszukiwarka