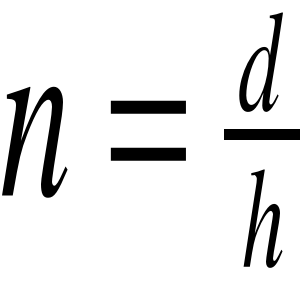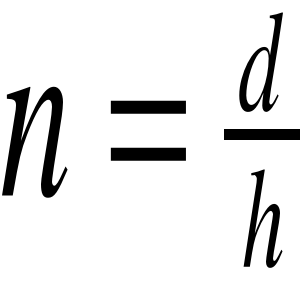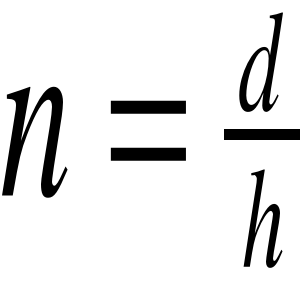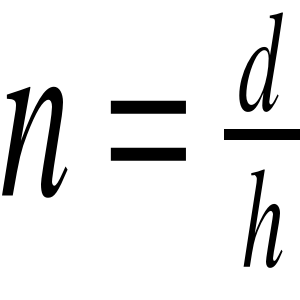WNiG
|
Bartosz Żychowski Marcin Żurek |
Rok: II |
Grupa: 6 |
Zespół: 5 |
|||
Temat: Współczynnik załamania światła dla ciał stałych. |
Nr ćwiczenia: 51 |
||||||
|
Data wykonania: 18.03.2008 |
Data oddania:
|
Data zaliczenia: |
Ocena:
|
|||
Cel ćwiczenia.
Celem ćwiczenia jest wyznaczenie współczynnika załamania światła dla różnych materiałów metodą obserwacji pozornych zmian grubości płytki, wynikłych z faktu istnienia tego współczynnika i porównanie tych wielkości z rzeczywistą grubością zmierzoną śrubą mikrometryczną. Należy także zbadać wpływ długości fali padającej wiązki świetlnej na wartość tego współczynnika.
Wstęp teoretyczny.
![]()
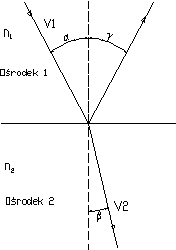
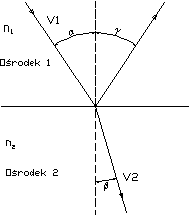
Wiązka światła przechodząc przez granicę dwóch ośrodków o różnych właściwościach optycznych, wyrażających się przez różną wartość współczynnika załamania, zostaje częściowo odbita, a częściowo przechodzi przez tą granicę jednocześnie ulegając załamaniu. Wartość współczynnika załamania ośrodka 2 względem ośrodka 1 można wyznaczyć, stosując prawo Snella :
gdzie ![]()
jest szukanym współczynnikiem załamania, a ![]()
i ![]()
współczynnikami załamania poszczególnych ośrodków. Dla przejścia światła z ośrodka optycznie rzadszego (np. powietrza) do gęstszego (np. szkła) wartość współczynnika załamania jest większa od 1. Kąt β jest wtedy mniejszy niż kąt α (czyli następuje załamanie do normalnej). Dla przejścia w drugą stronę, jest dokładnie na odwrót.
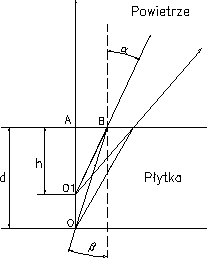
Na skutek zjawiska załamania, kształt i wymiary geometryczne przedmiotów znajdujących się w ośrodku optycznie gęstszym obserwowanych z ośrodka optycznie rzadszego wydają się być inne niż są w rzeczywistości (np. prosty kawałek drutu włożony do wody wygląda, jakby był wygięty w miejscu styku wody z powietrzem). Zjawisko to wyjaśnione jest na rysunku 2. Promień OA przechodzi przez płytkę bez załamania gdyż jest do niej prostopadły. Promień OB porusza się w płytce pod kątem β do normalnej, a przy przejściu do powietrza załamuje się i wychodzi pod kątem α. Rysując przedłużenie tego promienia w powietrzu, widzimy, że przecina się ono z promieniem OA w punkcie O1. Tak więc obserwator widzi odległość AO1=h, jako pozorną grubość płytki. Rzeczywistą grubością jest natomiast odległość OA=d, Poprzez porównanie tych odległości można wyznaczyć współczynnik załamania materiału z którego została wykonana płytka względem powietrza.
Zależność tą można wyznaczyć z prawa Snella.
![]()
Dla małych kątów można przyjąć.
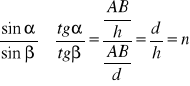
Opracowanie wyników pomiarów:
Materiał |
SZKŁO |
||||
Lp. |
Grubość rzeczywista |
Wskazanie czujnika |
Grubość pozorna |
Współczynnik załamania |
|
|
d [mm] |
ad [mm] |
ag [mm] |
h=ad-ag [mm] |
|
1. |
1,63 |
7,92 |
6,87 |
1,05 |
1,55 |
2. |
1,65 |
7,92 |
6,90 |
1,02 |
1,62 |
3. |
1,63 |
7,91 |
6,90 |
1,01 |
1,61 |
4. |
1,65 |
7,93 |
6,90 |
1,03 |
1,60 |
5. |
1,66 |
7,94 |
6,91 |
1,03 |
1,61 |
6. |
1,66 |
7,94 |
6,91 |
1,03 |
1,61 |
7. |
1,62 |
7,96 |
6,93 |
1,03 |
1,57 |
8. |
1,63 |
7,95 |
6,91 |
1,04 |
1,57 |
|
|
|
|
Wartość średnia ¯n
|
1,59 |
Materiał |
PLEKSIA |
||||
Lp. |
Grubość rzeczywista |
Wskazanie czujnika |
Grubość pozorna |
Współczynnik załamania |
|
|
d [mm] |
ad [mm] |
ag [mm] |
h=ad-ag [mm] |
|
1. |
1,49 |
8,08 |
7,09 |
0,99 |
1,51 |
2. |
1,47 |
8,07 |
7,07 |
1,00 |
1,47 |
3. |
1,46 |
8,09 |
7,09 |
1,00 |
1,46 |
4. |
1,48 |
8,09 |
7,10 |
0,99 |
1,49 |
5. |
1,49 |
8,10 |
7,10 |
1,00 |
1,49 |
6. |
1,47 |
8,09 |
7,09 |
1,00 |
1,47 |
7. |
1,48 |
8,10 |
7,07 |
1,03 |
1,44 |
8. |
1,47 |
8,08 |
7,08 |
1,00 |
1,47 |
|
|
|
|
Wartość średnia ¯n
|
1,48 |
dśr = 1,64 mm
Materiał |
SZKŁO + FILTR ZIELONY |
||||
Lp. |
Grubość rzeczywista |
Wskazanie czujnika |
Grubość pozorna |
Współczynnik załamania |
|
|
d [mm] |
ad [mm] |
ag [mm] |
h=ad-ag [mm] |
|
1. |
1,64 |
7,97 |
6,93 |
1,04 |
1,58 |
2. |
1,64 |
7,95 |
6,92 |
1,03 |
1,59 |
3. |
1,64 |
7,96 |
6,93 |
1,03 |
1,59 |
4. |
1,64 |
7,97 |
6,94 |
1,03 |
1,59 |
5. |
1,64 |
7,98 |
6,95 |
1,03 |
1,59 |
6. |
1,64 |
7,96 |
6,95 |
1,01 |
1,62 |
|
|
|
|
Wartość średnia ¯n
|
1,59 |
Materiał |
SZKŁO + FILTR ŻÓŁTY |
||||
Lp. |
Grubość rzeczywista |
Wskazanie czujnika |
Grubość pozorna |
Współczynnik załamania |
|
|
d [mm] |
ad [mm] |
ag [mm] |
h=ad-ag [mm] |
|
1. |
1,64 |
7,93 |
6,91 |
1,02 |
1,61 |
2. |
1,64 |
7,94 |
6,93 |
1,01 |
1,62 |
3. |
1,64 |
7,95 |
6,94 |
1,01 |
1,62 |
4. |
1,64 |
7,96 |
6,92 |
1,04 |
1,58 |
5. |
1,64 |
7,96 |
6,94 |
1,02 |
1,61 |
6. |
1,64 |
7,96 |
6,93 |
1,03 |
1,59 |
|
|
|
|
Wartość średnia ¯n
|
1,61 |
Oszacowanie niepewności standardowej typu B
![]()
Oszacowanie niepewności standardowej typu C
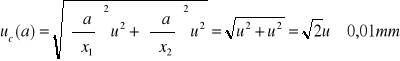
Tak wiec grubość pozorna płytki szklanej wyznaczona powyższą metoda wynosi 1,18(![]()
).
Średni współczynnik załamania liczony jest z wzoru ![]()
.
Średnia pozorna grubość płytki liczona jest z wzoru ![]()
.
Ponieważ wyznaczając współczynnik załamania, dokonujemy dwóch pomiarów grubości płytki (rzeczywistej d i pozornej h), i oba są obarczone błędem, więc błąd względny pomiaru tego współczynnika możemy wyznaczyć korzystając z prawa przenoszenia błędów. Prawo to w ogólnej postaci gdy dokonujemy pośredniego pomiaru wielkości y, zależnej od wielkości ![]()
mierzonych pośrednio i obarczonych błędami ![]()
.ma wygląd:
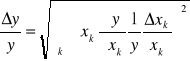
,
W naszym przypadku pośrednio mierzymy współczynnik załamania n, związany wzorem![]()
z bezpośrednio mierzonymi grubościami płytki: pozorną h i rzeczywistą d. Podany wzór przyjmie więc postać:
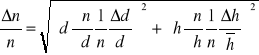
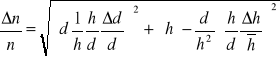
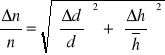
Błąd względny podaje się w procentach i w tym celu stosuje się wzór:![]()
Błąd bezwzględny![]()
liczymy mnożąc błąd względny przez średnią wartość współczynnika załamania:
Wykorzystując podane wzory otrzymaliśmy dla poszczególnych płytek wartości:
Dla płytki szklanej
Średnia pozorna grubość płytki : ![]()
Średni współczynnik załamania: ![]()
Błąd względny: ![]()
Błąd bezwzględny: ![]()
Po uwzględnieniu tych obliczeń ostatecznie można powiedzieć, że zmierzyliśmy wartość współczynnika załamania ![]()
Dla płytki z pleksi
Średnia pozorna grubość płytki : ![]()
Średni współczynnik załamania: ![]()
Błąd względny: ![]()
Błąd bezwzględny: ![]()
Po uwzględnieniu tych obliczeń ostatecznie można powiedzieć, że zmierzyliśmy wartość współczynnika załamania ![]()
Pomiary w świetle monochromatycznym.
Aby sprawdzić czy współczynnik załamania zależy od długości fali zmierzyliśmy grubości pozorne dla światła monochromatycznego o różnych długościach fali, po czym sporządziliśmy wykres ![]()
. Pomiary wykonaliśmy dla płytki szklanej o grubości rzeczywistej ![]()
.
* |
h |
n |
zielone |
|
1,567 |
żółte |
|
1,4 |
![]()
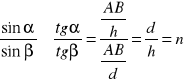
![]()
Wyszukiwarka