6.2. Zagadnienia brzegowe dla równań różniczkowych
zwyczajnych
6.2.1. Wstęp
Obok zagadnień początkowych dla równań różniczkowych zwyczajnych w praktyce występują także często zagadnienia ogólniejsze - zagadnienia brzegowe. Szukane jest wówczas rozwiązanie ![]()
układu równań (6.4) spełniające warunki brzegowe postaci:
![]()
gdzie i są macierzami kwadratowymi stopnia n o stałych elementach, a C1 i C2 - zadanymi wektorami kolumnowymi.
Podczas gdy zagadnienia początkowe mają zwykle dokładnie jedno rozwiązanie, gdy funkcje ( x , Y ) ( i = 1, 2, ..., n) są ograniczone i ciągłe oraz spełniają warunek Lipschitza względem argumentów: [26], zagadnienia brzegowe mogą nie mieć żadnego rozwiązania lub mogą mieć ich wiele. Przykładowo zagadnienie brzegowe:
ma nieskończenie wiele rozwiązań postaci
gdzie A jest dowolną stałą. Natomiast zagadnienie brzegowe:
ma dla jedyne rozwiązanie
![]()
a dla nie ma w ogóle rozwiązań. Chociaż nie można podać żadnego ogólnego twierdzenia o istnieniu i jednoznaczności rozwiązań zagadnień brzegowych, to na ogół istnieją ich rozwiązania, gdyż zwykle zagadnienia te opisują jakieś zjawiska fizyczne.
Metody rozwiązywania zagadnień brzegowych, podobnie jak metody rozwiązywania zagadnień początkowych, można podzielić również na metody analityczne, analityczno-numeryczne i dyskretne. Mogą one dotyczyć rozwiązywania pierwotnych zagadnień brzegowych lub też równoważnych im zagadnień początkowych, sformułowań wariacyjnych oraz równań całkowych.
Przy rozwiązywaniu zagadnień brzegowych mogą być stosowane metody analityczne polegające na rozwijaniu rozwiązań w szeregi potęgowe lub wykorzystaniu metody kolejnych przybliżeń Picarda.
Do metod analityczno-numerycznych można zaliczyć liczne metody wariacyjne jak:
- metoda najmniejszych kwadratów,
- metoda Galerkina,
- metoda Ritza
oraz metodę kollokacji, w której żąda się, aby rozwiązanie, przedstawione w postaci kombinacji liniowej funkcji bazowych, było spełnione w określonych punktach przedziału ![]()
Najważniejszymi metodami dyskretnymi rozwiązywania zagadnień brzegowych dla równań różniczkowych są:
- prosta metoda strzałów, w której dodatkowe parametry występujące w rozwiązaniu równoważnego zagadnienia początkowego są wyznaczane z warunków brzegowych,
- wielocelowa metoda strzałów [29, 34], polegająca na podzieleniu przedziału [a, b] na pewną liczbę podprzedziałów, w których rozwiązuje się niezależne zagadnienia początkowe z dodatkowymi parametrami wyznaczanymi z warunków ciągło-
ści rozwiązania i jego pochodnej. Jej zaletą jest możliwość osiągnięcia bardzo dużej dokładności obliczeń,
- specjalne metody wielokrokowe liniowe opracowane do bezpośredniego rozwiązywania zagadnień brzegowych [29],
- metody różnicowe, u których podstaw leży idea zastąpienia pochodnych przez odpowiednie ilorazy różnicowe,
- metoda elementów skończonych, polegająca na podziale przedziału ![]()
na pewną liczbę elementów, dla których przyjęte rozwiązania przybliżone wyznacza się ze sformułowań wariacyjnych [35].
Przedstawimy dwie metody odznaczające się prostymi algorytmami obliczeniowymi, pozwalającymi na uzyskanie wyników z dokładnością wystarczającą w wielu zastosowaniach praktycznych. Są to:
- metoda różnic skończonych,
- metoda kollokacji funkcjami sklejanymi.
Zagadnienia brzegowe są formułowane zwykle dla równań drugiego, trzeciego i czwartego rzędu lub też ich układów. Ograniczymy się do wyznaczenia rozwiązania równania liniowego drugiego rzędu
![]()
(6.82)
z dwupunktowymi liniowymi warunkami brzegowymi:
(6.83)
6.2.2. Metoda różnic skończonych
Aby przekształcić zagadnienie różniczkowe (6.82) - (6.83) na zagadnienie różnicowe podzielimy odcinek ![]()
na n równych części o długości ![]()
(6.84)
a następnie zastąpimy pochodne i ich centralnymi ilorazami różnicowymi (5.6) i (5.15). Wprowadzając oznaczenia skrócone:
![]()
(6.85)
otrzymujemy dla każdego (i = 1, 2, ..., n −1) zamiast równania różniczkowe-go (6.82) następujące równanie różnicowe
![]()
Stąd po przekształceniu dochodzimy do układu równań liniowych z trójdiagonalną macierzą współczynników
(6.86)
gdzie:
Dla zachowania tego samego rzędu aproksymacji warunków brzegowych (6.83) pochodne i zastąpimy ilorazami różnicowymi (5.8) i (5.9):
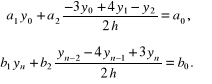
(6.87)
Z równań różnicowych (6.87) wyznaczamy:
![]()
(6.88)
gdzie:
![]()
![]()
![]()
![]()
![]()
Uwzględnienie zależności (6.88) wynikających z aproksymacji warunków brzegowych powoduje korektę następujących współczynników układu (6.86):
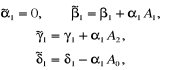
(6.89a)
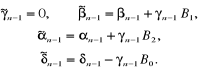
(6.89b)
W przypadkach wielu zagadnień fizyki matematycznej występują jednakże prostsze warunki brzegowe:
lub
i wtedy wzory (6.88) i (6.89) znacznie się upraszczają.
*
{Program 6.6}
unit Obliczenia;
interface
uses
Windows, Messages, SysUtils, Classes, Graphics, Controls,
Forms, Dialogs, StdCtrls, Buttons;
. . . . . . . . . . . . . . . . .
var
Form3: TForm3;
a,a0,a1,a2,b,b0,b1,b2,bl,h,hp,x,ui,p,p1,p2: Real;
al,be,ga,de,q,u,y: array[0..100] of Real;
Ad,Bd: array[0..3] of Real;
i,n,n1: Integer;
plik: Text;
implementation
uses Ustawienia, Informacje, Grafika, Podglad;
{$R *.DFM}
function urr(x: Real): Real;
begin
urr:=-2*x;
end;
function vrr(x: Real): Real;
begin
vrr:=-2;
end;
function wrr(x: Real): Real;
begin
wrr:=-4*x;
end;
function yd(x: Real): Real;
begin
yd:=x+Exp(x*x);
end;
. . . . . . . . . . . . .
procedure TForm3.BitBtn1Click(Sender: TObject);
label powt;
begin
Form2.Show;
AssignFile(plik,Edit10.Text);
Rewrite(plik); Writeln(plik,'PROGRAM 6.6.');
Writeln(plik,'Zagadnienie brzegowe dla równania');
Writeln(plik,'różniczkowego zwyczajnego.');
Writeln(plik,'Metoda różnic skończonych.');
Writeln(plik); a:=StrToFloat(Edit1.Text);
b:=StrToFloat(Edit2.Text); n:=StrToInt(Edit3.Text);
a0:=StrToFloat(Edit4.Text); a1:=StrToFloat(Edit5.Text);
a2:=StrToFloat(Edit6.Text); b0:=StrToFloat(Edit7.Text);
b1:=StrToFloat(Edit8.Text); b2:=StrToFloat(Edit9.Text);
Writeln(plik,'Liczba podprzedziałów: n = ',n:3);
Writeln(plik,'Początek przedziału: a = ',a:13);
Writeln(plik,'Koniec przedziału: b = ',b:13);
Writeln(plik,'Stałe określające warunki brzegowe:');
Writeln(plik,' - a1, a2, a0 = ',a1:9:6,a2:11:6,a0:11:6);
Writeln(plik,' - b1, b2, b0 = ',b1:9:6,b2:11:6,b0:11:6);
Writeln(plik); Writeln(plik,'Obliczone wartości funkcji:');
Writeln(plik,' i x[i] y[i] błąd');
n1:=n-1; h:=(b-a)/n; hp:=1/h;
for i:=1 to n1 do begin
x:=a+i*h; ui:=urr(x);
al[i]:=hp*(hp-ui/2); be[i]:=-2*hp*hp+vrr(x);
ga[i]:=hp*(hp+ui/2); de[i]:=wrr(x);
end;
Ad[3]:=2*h*a1-3*a2; Ad[0]:=2*h*a0/Ad[3];
Ad[1]:=-4*a2/Ad[3]; Ad[2]:=a2/Ad[3];
Bd[3]:=2*h*b1+3*b2; Bd[0]:=2*h*b0/Bd[3];
Bd[1]:=4*b2/Bd[3]; Bd[2]:=-b2/Bd[3];
p1:=al[1]; p2:=ga[n1]; al[1]:=0; ga[n1]:=0;
be[1]:=be[1]+p1*Ad[1]; ga[1]:=ga[1]+p1*Ad[2];
de[1]:=de[1]-p1*Ad[0]; be[n1]:=be[n1]+p2*Bd[1];
al[n1]:=al[n1]+p2*Bd[2]; de[n1]:=de[n1]-p2*Bd[0];
q[0]:=0; u[0]:=0;
for i:=1 to n1 do begin
p:=be[i]+al[i]*q[i-1];
q[i]:=-ga[i]/p;
u[i]:=(de[i]-al[i]*u[i-1])/p;
end;
y[n1]:=u[n1];
for i:=n-2 downto 1 do
y[i]:=q[i]*y[i+1]+u[i];
y[0]:=Ad[0]+Ad[1]*y[1]+Ad[2]*y[2];
y[n]:=Bd[0]+Bd[1]*y[n1]+Bd[2]*y[n-2];
if (a2<>0) and (b2<>0) then
for i:=0 to n do
y[i]:=y[i]-y[0]+yd(a);
for i:=0 to n do begin
x:=a+i*h; bl:=yd(x)-y[i];
Writeln(plik,i:3,' ',x:13,' ',y[i]:18,' ',bl:13);
end;
Writeln(plik); CloseFile(plik);
Form2.Wyniki.Lines.LoadFromFile(Edit10.Text);
end;
. . . . . . . . . . . . . . . . . . . . . . .
Rys. 6.7
W programie 6.6 wyznaczane jest przybliżone rozwiązanie równania różniczkowego
![]()
(6.90)
spełniające dwa rodzaje warunków brzegowych (6.83):
a)
![]()
(6.91a)
b)
![]()
(6.91b)
Funkcje ![]()
i obliczane są w procedurach funkcyjnych urr(x), vrr(x) i wrr(x). Wartości określające początek i koniec przedziału ![]()
liczbę podprzedziałów n oraz stałe występujące w warunkach brzegowych (6.83) wczytywane są z formularza Dane (rys. 6.7). Rozwiązanie numeryczne porównywane jest z rozwiązaniem dokładnym
![]()
(6.92)
obliczanym w procedurze funkcyjnej yd(x). Uzyskane wyniki obliczeń dla n = 40 są następujące:
PROGRAM 6.6.
Zagadnienie brzegowe dla równania
różniczkowego zwyczajnego.
Metoda różnic skończonych.
Liczba podprzedziałów: n = 40
Początek przedziału: a = -1.0000E+0000
Koniec przedziału: b = 1.0000E+0000
Stałe określające warunki brzegowe:
- a1, a2, a0 = 1.000000 0.000000 1.718282
- b1, b2, b0 = 1.000000 0.000000 3.718282
Obliczone wartości funkcji:
i x[i] y[i] błąd
0 -1.0000E+0000 1.718281828E+0000 5.8208E-0011
1 -9.5000E-0001 1.515869944E+0000 -1.1013E-0004
2 -9.0000E-0001 1.348120092E+0000 -2.1211E-0004
3 -8.5000E-0001 1.209880372E+0000 -3.0465E-0004
4 -8.0000E-0001 1.096868256E+0000 -3.8738E-0004
5 -7.5000E-0001 1.005515093E+0000 -4.6044E-0004
6 -7.0000E-0001 9.328405441E-0001 -5.2432E-0004
7 -6.5000E-0001 8.763509434E-0001 -5.7972E-0004
8 -6.0000E-0001 8.339568185E-0001 -6.2740E-0004
9 -5.5000E-0001 8.039058310E-0001 -6.6815E-0004
10 -5.0000E-0001 7.847281608E-0001 -7.0274E-0004
11 -4.5000E-0001 7.751919778E-0001 -7.3189E-0004
12 -4.0000E-0001 7.742671278E-0001 -7.5626E-0004
13 -3.5000E-0001 7.810955423E-0001 -7.7642E-0004
14 -3.0000E-0001 7.949671834E-0001 -7.9290E-0004
15 -2.5000E-0001 8.153005848E-0001 -8.0613E-0004
16 -2.0000E-0001 8.416272385E-0001 -8.1646E-0004
17 -1.5000E-0001 8.735792418E-0001 -8.2421E-0004
18 -1.0000E-0001 9.108797475E-0001 -8.2958E-0004
19 -5.0000E-0002 9.533358688E-0001 -8.3274E-0004
20 2.2737E-0013 1.000833784E+0000 -8.3378E-0004
21 5.0000E-0002 1.053335869E+0000 -8.3274E-0004
22 1.0000E-0001 1.110879747E+0000 -8.2958E-0004
23 1.5000E-0001 1.173579242E+0000 -8.2421E-0004
24 2.0000E-0001 1.241627239E+0000 -8.1646E-0004
25 2.5000E-0001 1.315300585E+0000 -8.0613E-0004
26 3.0000E-0001 1.394967183E+0000 -7.9290E-0004
27 3.5000E-0001 1.481095542E+0000 -7.7642E-0004
28 4.0000E-0001 1.574267128E+0000 -7.5626E-0004
29 4.5000E-0001 1.675191978E+0000 -7.3189E-0004
30 5.0000E-0001 1.784728161E+0000 -7.0274E-0004
31 5.5000E-0001 1.903905831E+0000 -6.6815E-0004
32 6.0000E-0001 2.033956818E+0000 -6.2740E-0004
33 6.5000E-0001 2.176350943E+0000 -5.7972E-0004
34 7.0000E-0001 2.332840544E+0000 -5.2432E-0004
35 7.5000E-0001 2.505515093E+0000 -4.6044E-0004
36 8.0000E-0001 2.696868256E+0000 -3.8738E-0004
37 8.5000E-0001 2.909880372E+0000 -3.0465E-0004
38 9.0000E-0001 3.148120092E+0000 -2.1211E-0004
39 9.5000E-0001 3.415869944E+0000 -1.1013E-0004
40 1.0000E+0000 3.718281828E+0000 5.8208E-0011
PROGRAM 6.6.
Zagadnienie brzegowe dla równania
różniczkowego zwyczajnego.
Metoda różnic skończonych.
Liczba podprzedziałów: n = 40
Początek przedziału: a = -1.0000E+0000
Koniec przedziału: b = 1.0000E+0000
Stałe określające warunki brzegowe:
- a1, a2, a0 = 1.000000 0.000000 1.718282
- b1, b2, b0 = 1.000000 -1.000000 -2.718282
Obliczone wartości funkcji:
i x[i] y[i] błąd
0 -1.0000E+0000 1.718281828E+0000 5.8208E-0011
1 -9.5000E-0001 1.516268491E+0000 -5.0868E-0004
2 -9.0000E-0001 1.348882943E+0000 -9.7496E-0004
3 -8.5000E-0001 1.210979801E+0000 -1.4040E-0003
4 -8.0000E-0001 1.098282094E+0000 -1.8012E-0003
5 -7.5000E-0001 1.007225952E+0000 -2.1713E-0003
6 -7.0000E-0001 9.348351974E-0001 -2.5190E-0003
7 -6.5000E-0001 8.786198334E-0001 -2.8486E-0003
8 -6.0000E-0001 8.364936683E-0001 -3.1643E-0003
9 -5.5000E-0001 8.067073461E-0001 -3.4697E-0003
10 -5.0000E-0001 7.877938068E-0001 -3.7684E-0003
11 -4.5000E-0001 7.785238246E-0001 -4.0637E-0003
12 -4.0000E-0001 7.778697527E-0001 -4.3589E-0003
13 -3.5000E-0001 7.849759864E-0001 -4.6569E-0003
14 -3.0000E-0001 7.991349588E-0001 -4.9607E-0003
15 -2.5000E-0001 8.197677300E-0001 -5.2733E-0003
16 -2.0000E-0001 8.464084214E-0001 -5.5976E-0003
17 -1.5000E-0001 8.786919132E-0001 -5.9369E-0003
18 -1.0000E-0001 9.163443451E-0001 -6.2942E-0003
19 -5.0000E-0002 9.591760779E-0001 -6.6730E-0003
20 2.2737E-0013 1.007076860E+0000 -7.0769E-0003
21 5.0000E-0002 1.060013026E+0000 -7.5099E-0003
22 1.0000E-0001 1.118026632E+0000 -7.9765E-0003
23 1.5000E-0001 1.181236488E+0000 -8.4815E-0003
24 2.0000E-0001 1.249841135E+0000 -9.0304E-0003
25 2.5000E-0001 1.324123862E+0000 -9.6294E-0003
26 3.0000E-0001 1.404459944E+0000 -1.0285E-0002
27 3.5000E-0001 1.491326362E+0000 -1.1007E-0002
28 4.0000E-0001 1.585314365E+0000 -1.1803E-0002
29 4.5000E-0001 1.687145318E+0000 -1.2685E-0002
30 5.0000E-0001 1.797690461E+0000 -1.3665E-0002
31 5.5000E-0001 1.917995305E+0000 -1.4757E-0002
32 6.0000E-0001 2.049309654E+0000 -1.5980E-0002
33 6.5000E-0001 2.193124424E+0000 -1.7353E-0002
34 7.0000E-0001 2.351216799E+0000 -1.8901E-0002
35 7.5000E-0001 2.525705599E+0000 -2.0651E-0002
36 8.0000E-0001 2.719119270E+0000 -2.2638E-0002
37 8.5000E-0001 2.934479493E+0000 -2.4904E-0002
38 9.0000E-0001 3.175404224E+0000 -2.7496E-0002
39 9.5000E-0001 3.446234972E+0000 -3.0475E-0002
40 1.0000E+0000 3.752194430E+0000 -3.3913E-0002
390 6. Równania różniczkowe zwyczajne i całkowe
6.2. Zagadnienia brzegowe dla równań różniczkowych zwyczajnych 387
Wyszukiwarka