REAKCJE JĄDROWE. PROMIENIOTWÓRCZOŚĆ.

PROMIENIOTWÓRCZOŚĆ NATURALNA I SZTUCZNA

Reakcjami jądrowymi nazywamy zjawiska, w których zachodzi zmiana składu lub stanu energetycznego jądra atomowego. Reakcje jądrowe możemy podzielić na spontaniczne (promieniotwórczość naturalna) i wymuszone (promieniotwórczość sztuczna). Pierwsze przebiegają całkowicie samorzutnie — należy do nich np. rozpad jąder atomów nietrwałych. Drugie mogą zachodzić tylko po poddaniu pierwiastka odpowiednim przemianom — przykładami takich ciał promieniotwórczych mogą być produkty reakcji jądrowych. Pierwiastki wytworzone w ten sposób nazywamy sztucznymi pierwiastkami promieniotwórczymi.

PRAWO ROZPADU PROMIENIOTWÓRCZEGO

Mianem rozpadu promieniotwórczego określamy samorzutne przemiany jąder nietrwałych, czyli spontaniczne reakcje jądrowe. Rozpad promieniotwórczy jest procesem przypadkowym, podlegającym prawom rachunku prawdopodobieństwa. Jeżeli zatem początkową liczbę atomów nietrwałych w rozpatrywanej próbce oznaczymy jako N₀, to po upływie czasu t ilość N atomów, które jeszcze nie uległy rozpadowi, będzie podawało równanie:

Zależność ta nosi nazwę prawa rozpadu promieniotwórczego. Symbol t w powyższym równaniu oznacza czas mierzony od momentu zerowego (tzn. tego, w którym rozpoczynał się proces rozpadu), e jest podstawą logarytmu naturalnego, λ natomiast — tzw. stałą rozpadu. Stała ta jest wielkością charakterystyczną dla danego rozpadu, a konkretnie danego nuklidu promieniotwórczego. Im większa jest jej wartość, tym więcej jąder danego nuklidu ulega rozpadowi w tej samej jednostce czasu.

Czas, w ciągu którego rozpadnie się połowa jąder promieniotwórczych istniejących w momencie zerowym, nazywamy okresem rozpadu połowicznego, okresem półrozpadu lub czasem połowicznego zaniku nuklidu promieniotwórczego. Czas połowicznego zaniku oznaczamy symbolem T i obliczamy go ze wzoru:

Dla naturalnych pierwiastków promieniotwórczych czas połowicznego zaniku zawiera się w granicach od około 3·10^-7 sekundy do około 1,4 · 10¹⁷ lat — widać zatem, że wartości te są bardzo rozbieżne.

Prawo rozpadu promieniotwórczego, jak wszystkie prawa podlegające rachunkowi prawdopodobieństwa, jest całkowicie słuszne tylko w tym przypadku, gdy liczba rozpadów w określonym czasie t jest bardzo duża. Im mniejsza liczba rozpadów, tym większym odchyleniom ulega liczba jąder rozpadających się w poszczególnych przedziałach czasu.

AKTYWNOŚĆ NUKLIDU PROMIENIOTWÓRCZEGO

Aktywnością A nuklidu promieniotwórczego nazywamy stosunek:

gdzie ∆N jest liczbą przemian jądrowych zachodzących w czasie ∆t.

Jednostką aktywności jest bekerel (Bq), odpowiadający jednemu rozpadowi na sekundę. Wcześniej stosowaną jednostką był kiur (curie, Ci), liczący sobie 3,7 · 10¹⁰ Bq, czyli tyleż rozpadów na sekundę.

Aktywność danego preparatu promieniotwórczego możemy obliczyć ze wzoru:

gdzie λ jest stałą rozpadu,

a N oznacza liczbę atomów w preparacie.

Inaczej możemy zapisać go:

gdzie N_A jest liczbą Avogadra,

M — masą molową pierwiastka promieniotwórczego,

m — masą preparatu wyrażoną w gramach,

a T — okresem połowicznego rozpadu.

Aktywność właściwa jest to aktywność promieniotwórcza jednostki masy nuklidu, ewentualnie objętości lub powierzchni źródła promieniowania. Jednostkami aktywności właściwej są odpowiednio: Bq/kg, Bq/m³ i Bq/m².

PROMIENIOWANIE RENTGENOWSKIE

Promieniowanie rentgenowskie (promienie Roentgena, promieniowanie X), odkryte przez Roentgena w 1895 r., są to fale elektromagnetyczne zajmujące w widmie obszar między nadfioletem a promieniowaniem γ. Długość fali promieniowania rentgenowskiego mieści się w przedziale od 0,01 do 80 nm.

OTRZYMYWANIE PROMIENIOWANIA RENTGENTOWSKIEGO

Promieniowanie rentgenowskie powstaje podczas hamowania elektronów w materii. W praktyce otrzymujemy je w zespole urządzeń, zwanym aparaturą rentgenowską, której najważniejszą część stanowi lampa rentgenowska. Oprócz lampy rentgenowskiej aparatura zawiera również układ zasilania. Składa się on z dwóch niezależnych obwodów elektrycznych, tzw. obwodu wysokiego i niskiego napięcia, utworzonych przez źródła prądu, przewody i transformatory. W obydwu obwodach płynie prąd zmienny, którego prostowanie, tzn. przekształcanie w prąd stały, odbywa się wewnątrz lampy, pełniącej jednocześnie rolę prostownika. Bardzo często lampę rentgenowską wraz z przewodami i transformatorami zamyka się we wspólnej obudowie, wypełnionej olejem, i określa się łączną nazwą głowicy.

Lampa rentgenowska składa się z dwóch elektrod — katody i anody (antykatody) — umieszczonych we wspólnej obudowie (bańce szklanej lub metalowej), w której panuje ciśnienie rzędu 10^-4 Pa. Na zewnątrz obudowy znajduje się dodatkowa osłona ołowiana, pochłaniająca promieniowanie boczne. W osłonie tej znajduje się otwór — okienko, przez które wychodzi wiązka promieniowania X.

Obwód niskiego napięcia, zwany także obwodem żarzenia, podłączony jest wyłącznie do katody i służy do jej żarzenia. Dzięki temu obwodowi katoda uzyskuje wysoką temperaturę, pozwalającą na uwalnianie się z jej powierzchni elektronów w procesie termoemisji. Napięcie w tym obwodzie jest rzędu 10-12 V i może być zmieniane w niewielkich granicach dzięki opornikowi suwakowemu. Zmianie natężenia w obwodzie niskiego napięcia towarzyszy zmiana natężenia otrzymywanego promieniowania rentgenowskiego, ponieważ im wyższa temperatura katody, tym więcej elektronów uwalnia się z jej powierzchni.

Obwód wysokiego napięcia łączy katodę i anodę, dzięki czemu powstaje między nimi pole elektryczne przyspieszające elektrony. Napięcie w tym obwodzie liczy od kilku do kilkuset tysięcy woltów, a zmieniamy je przy pomocy autotransformatora. Zmiana wysokiego napięcia powoduje zmianę zarówno natężenia, jak i „twardości” (długości fali) otrzymywanego promieniowania X. Wzrostowi napięcia odpowiada wzrost maksymalnej energii promieniowania i przesuwanie się maksimum energetycznego w stronę fal bardziej twardych, czyli mających mniejszą długość.

Zasada działania lampy rentgenowskiej jest następująca: z powierzchni katody na skutek termoemisji uwalniają się elektrony, które następnie są silnie przyspieszane w polu elektrycznym znajdującym się między katodą a anodą. Po dojściu do anody następuje hamowanie elektronów w jej materiale.

Strumień elektronów dochodzący do anody nie jest niczym innym, jak prądem elektrycznym, któremu towarzyszy pole magnetyczne. Podczas hamowania elektronów wewnątrz anody, jak wynika z praw elektromagnetyzmu, następuje gwałtowna zmiana natężenia tego pola. Ponieważ zaś wiemy, że zmiennemu polu magnetycznemu towarzyszy zawsze zmienne pole elektryczne, wewnątrz lampy rentgenowskiej powstają krótkotrwałe, zmienne zaburzenia, rozchodzące się w przestrzeni w postaci krótkich impulsów — fal elektromagnetycznych. Tymi falami są właśnie promienie X, których energia jest przekształconą energią kinetyczną elektronów.

Warto dodać, że zaledwie 1% całkowitej energii kinetycznej elektronów ulega przemianie w energię fali elektromagnetycznej. Aż 99% zamienia się w energię ruchów cieplnych materii, czyli zużywane jest na ogrzanie anody. Dlatego też anoda jest zazwyczaj masywnym miedzianym blokiem, wyłożonym wkładką wolframową i chłodzonym od zewnątrz wodą lub za pomocą promiennika żeberkowego.

WIDMO CIĄGŁE PROMIENIOWANIA X

Podczas hamowania elektronów w materiale anody w sposób wytłumaczony przy opisie działania lampy rentgenowskiej powstają fale elektromagnetyczne, czyli promienie X. Ten rodzaj promieniowania nazywamy promieniowaniem hamowania, a jego widmo — widmem ciągłym. Na wykresie rozkładu natężeń w zależności od długości fali emitowanej widmo to przedstawia się następująco:

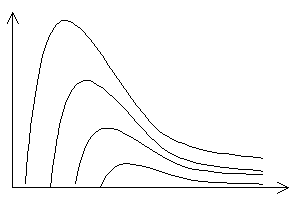
Poszczególne linie odpowiadają różnym wartościom napięcia między katodą a anodą — linia A przedstawia widmo ciągłe dla napięcia o najwyższej wartości, linia D — dla napięcia o wartości najniższej. Widać stąd, że im wyższe napięcie, tym większa jest maksymalna energia promieniowania i tym mniejsza długość fali, na którą przypada maksimum tej energii. Wyjaśnia się zatem, dlaczego zwiększanie napięcia wysokiego w aparaturze rentgenowskiej powoduje wzrost natężenia i twardości promieniowania rentgenowskiego.

Analizując powyższy wykres, warto zwrócić uwagę na jeszcze jedną rzecz: od strony fal krótszych widmo ciągłe jest wyraźnie ograniczone. Oznacza to, że dla każdego napięcia emisja fal krótkich jest możliwa tylko w pewnym zakresie, czyli że w procesie hamowania elektronów w anodzie niemożliwe jest uzyskanie promieniowania o długości fali mniejszej niż pewna minimalna długość λ_min, zwana krótkofalową granicą widma ciągłego. Od strony fal długich podobne zjawisko nie występuje — ze wzrastającą długością energia fal rentgenowskich jest coraz mniejsza, lecz nie ma swojej ostrej granicy.

Istnienie krótkofalowej granicy widma ciągłego wyjaśnia teoria kwantów w następujący sposób: wiemy, że elektrony przyspieszane w polu elektrycznym o stałym napięciu nabywają energię kinetyczną E_k równą iloczynowi tego napięcia i swego ładunku:

Energia E_k podczas hamowania elektronu zmienia się, co już było zasygnalizowane, zarówno w energię kwantu promieniowania rentgenowskiego (E = hv), jak i w energię ruchów cieplnych atomów anody:

Jasne jest, że im większa część energii kinetycznej elektronu ulegnie przemianie w energię promieniowania, tym większa będzie energia kwantu, a mniejsza długość fali, zgodnie z prawem Plancka:

Jest jednak jasne, że kwant promieniowania rentgenowskiego nie może uzyskać energii większej od energii kinetycznej elektronu. Co najwyżej może ona równa E_k — w przypadku, gdy elektron całą swoją energię przekazuje promieniowaniu, nie powodując ruchów cieplnych atomów anody (Q = 0). Proces taki możemy opisać:

a więc :

dla elektronu przyspieszanego napięciem U o określonej, stałej wartości.

Przekształcając powyższą zależność, otrzymujemy:

Wielkość λ jest wartością λ_min — krótkofalową granicą widma ciągłego.

Ponieważ z czterech wielkości występujących w powyższym wzorze jedynie U nie jest żadną stałą, możemy zapisać go inaczej:

gdzie k traktujemy jako stałą o wartości około 1,24 nm · kV (gdy napięcie U wyrazimy w kV, wartość λ_min otrzymamy w nm).

Przy opisie działania lampy rentgenowskiej wspomniano, że natężenie otrzymywanego promieniowania X zależy od również natężenia prądu w obwodzie żarzenia. Zależność tę przedstawia wykres:

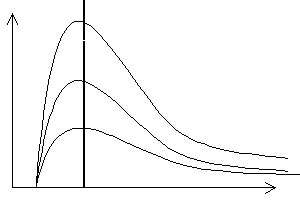
Wartości I₁, I₂ i I₃ odpowiadają kolejno: największemu, średniemu i najmniejszemu natężeniu prądu w obwodzie żarzenia. Z wykresu powyższego widać zatem, że zmiana tego natężenia powoduje zmianę natężenia promieniowania X, lecz w żaden sposób nie wiąże się ze zmianą długości jego fal.

WIDMO CHARAKTERYSTYCZNE PROMIENIOWANIA X

Przy odpowiednio wysokich napięciach między katodą a anodą może się jednak zdarzyć, że energia kinetyczna elektronów jest na tyle duża, aby mogły one wniknąć do wnętrza atomów anody. Taki elektron podczas zderzenia oddaje swoją energię jednemu z bliskich jądra elektronów, który wskutek tego opuszcza atom. Wolne miejsce zapełnia elektron z warstwy o wyższej energii, którego miejsce zajmuje kolejny przechodzący z wyższej warstwy itd., itd. Kolejne przejścia zgodnie z założeniami Bohra powodują emisję kwantów energii hv, podobnie jak dla widm optycznych. Powstaje wobec tego widmo liniowe promieniowania X — tak zwane widmo charakterystyczne. Nazwa bierze się stąd, że widmo to różni się dla różnych materiałów anody, czyli dla różnych pierwiastków.

W widmie charakterystycznym wyróżnić możemy poszczególne serie widmowe: K, L, M… itd., w zależności od tego, z którego poziomu energetycznego atomu wybijany jest elektron. Każda z tych serii dzieli się dodatkowo na linie, np. K_α, K_β, K_γ, L_α, L_β, L_γ… itd., ponieważ na miejsce elektronu wybitego ze swojego miejsca może wejść zarówno elektron z powłoki najbliższej (α), jak i z powłoki oddalonej o 2 lub 3 (β lub γ), a także z powłok dalszych.

Serią podstawową jest seria K, ponieważ elektrony bombardujące atomy anody najczęściej wybijają elektrony właśnie z tego poziomu. Serii tej zawsze towarzyszą jednak słabsze serie L, M i dalsze, ponieważ na miejsce uwolnione przez elektron na poziomie L przechodzi elektron z poziomu wyższego i tak dalej. W każdej z tych serii największe natężenie ma linia α, jako że prawdopodobieństwo zastąpienia wybitego elektronu elektronem z najbliższego poziomu energetycznego jest największe.

Układ linii widma charakterystycznego dla różnych pierwiastków jest podobny, ponieważ budowa wewnętrznych powłok elektronowych we wszystkich atomach jest taka sama. Zmianie ulega jednak częstość linii widmowych (długość fali emitowanego promieniowania). Stwierdzono, że im większa jest liczba atomowa pierwiastka, tym bardziej odpowiednie linie serii są przesunięte w stronę fal krótkich. Związek pomiędzy częstością linii widmowych a liczbą atomową Z pierwiastka anody została podana przez Moseleya w następującej postaci, zwanej prawem Moseleya:

gdzie b jest wartością stałą dla każdej serii (np. dla serii K b = 1, dla serii L b ≈ 7,5 itp.), A natomiast wiąże się z poziomami energetycznymi, między którymi zachodzi przejście elektronu:

gdzie n oznacza numer poziomu, na który elektron przechodzi,

m — numer poziomu, z którego elektron przechodzi,

a R — stałą Rydberga.

Wprowadzając wartość stałej A do prawa Moseleya, możemy wyliczyć częstość linii widmowych:

Widzimy zatem, że zależność między liczbą atomową pierwiastka a pierwiastkiem z częstości linii jego widma charakterystycznego jest liniowa.

ODDZIAŁYWANIE PROMIENIOWANIA Z MATERIĄ

PRZYCZYNY ODDZIAŁYWANIA PROMIENIOWANIA X I γ Z MATERIĄ

Wyróżniamy trzy zasadnicze rodzaje oddziaływania promieniowania elektromagnetycznego X i γ z materią. Wszystkie wiążą się z korpuskularnym charakterem promieniowania, czyli z istnieniem cząstek niosących skwantowaną energię — fotonów. Energia fotonu dana jest wzorem:

gdzie v jest częstością fali,

λ — jej długością,

c — prędkością światła w próżni,

a h — stałą Plancka.

Gdy promieniowanie wchodzi w kontakt z materią, fotony zderzają się z jej cząstkami elementarnymi (zarówno elektronami, jak i jądrami, jednak częściej z tymi pierwszymi) i na skutek tych zderzeń przekazują im swoją energię — w całości lub częściowo. Czasami zderzenie nie powoduje zmiany energii fotonu, lecz wyłącznie zmianę kierunku jego biegu. Niekiedy również może nastąpić rozpad fotonu — nie na skutek bezpośredniego zderzenia, lecz w wyniku dostania się w pole oddziaływań jąder atomowych. Analizując wszystkie rodzaje tych oddziaływań, efekty kontaktu promieniowania z materią możemy z grubsza podzielić na zjawiska absorpcji, rozpraszania oraz tworzenia par pozyton - elektron.

Łączny udział tych zjawisk w osłabianiu wiązki promieniowania w materii zależy od energii promieniowania. I tak: dla promieniowania o energii do 10 kV w materii zachodzi przeważnie absorpcja kwantów, dla promieniowania o energii od 200 kV do 2 MeV — ich rozpraszanie, wreszcie dla energii rzędu 20 MeV straty energii rozkładają się równomiernie między rozpraszanie a zjawisko tworzenia par pozyton - elektron.

ZJAWISKO ABSORPCJI

O absorpcji kwantu promieniowania mówimy wtedy, gdy energia tego kwantu podczas zderzenia zostanie całkowicie przekazana (najczęściej) elektronowi. Foton promieniowania przestaje wówczas istnieć, a jego energia, przejęta przez elektron, może wywołać rozmaite zjawiska. Należą do nich: jonizacja atomu (zjawisko fotoelektryczne zewnętrzne lub wewnętrzne), wzbudzenie optyczne atomu (fluorescencja lub fosforescencja), ewentualnie wzbudzenie wtórnego rentgenowskiego promieniowania charakterystycznego.

Jonizacją atomu nazywamy proces przejścia atomu w jon dodatni na skutek oderwania od niego elektronu. Proces ten wymaga dostarczenia pewnej ilości energii, zwanej energią jonizacji.

Proces jonizacji atomu pod wpływem światła nazywamy zjawiskiem fotoelektrycznym. Jeżeli przekazana elektronowi energia fotonu jest dostatecznie duża, elektron może wydostać się ze swojego poziomu energetycznego i opuścić atom. W zależności od tego, czy elektron wydostaje się wyłącznie poza obręb swojego atomu, pozostając jednak w obrębie substancji naświetlanej, czy też w ogóle opuszcza tę substancję, zjawiska fotoelektryczne dzielimy na wewnętrzne i zewnętrzne. W rezultacie zwiększenia się liczby swobodnych elektronów — czy to wewnątrz substancji naświetlanej, czy poza jej obrębem, w zależności od rodzaju zjawiska fotoelektrycznego — następuje wzrost przewodności tej substancji i (lub) przepływ prądu elektrycznego, zwanego fotoprądem.

Energia hv fotonu w zjawisku absorpcji zostaje zatem zużyta na pokonanie sił wiązania elektronu w atomie, wykonanie pracy wyjścia (w zjawisku fotoelektrycznym zewnętrznym) oraz na nadanie elektronowi pewnej energii kinetycznej. Wybity elektron, tzw. fotoelektron, zderza się z sąsiednimi atomami jonizując je, przy czym traci stopniowo swą energię kinetyczną i na koniec ulega rekombinacji (połączeniu z jonem dodatnim, w wyniku czego powstaje atom obojętny) lub przyłącza się do któregoś z obojętnych atomów, powodując powstanie jonu ujemnego.

ZJAWISKO ROZPRASZANIA

Zjawisko rozpraszania polega na zmianie kierunku biegu fotonu po zderzeniu z elektronem. Może ono zachodzić na dwa sposoby. Jeżeli foton po zderzeniu zachowuje całą swoją energię, mówimy o rozproszeniu zwykłym. Jeżeli jednak podczas zderzenia z elektronem foton przekazuje mu część swojej energii, mamy do czynienia z tzw. rozproszeniem komptonowskim (zjawisko Comptona).

Przypuśćmy, że na nieruchomy, swobodny elektron pada foton promieniowania o energii
E = hv₀. W wyniku zderzenia elektron przejmuje część energii fotonu — zostaje wówczas odrzucony z pewną prędkością pod kątem β do kierunku biegu fotonu przed zderzeniem. Foton z kolei zmienia swój kierunek biegu o inny kąt α. Jego energia, zmniejsza się o wartość oddaną elektronowi, co odpowiada wzrostowi długości fali. Energię tę określimy jako hv (gdzie v jest częstością fali po zderzeniu).

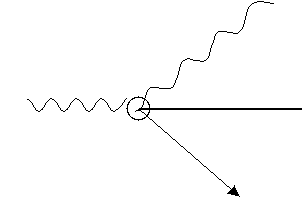
Zmianę długości fali możemy obliczyć w następujący sposób:

Przed zderzeniem prędkość elektronu jest równa 0, a więc i jego pęd równa się 0. Pęd fotonu wynosi natomiast
. Po zderzeniu wartości pędów wynoszą odpowiednio mv i
. Zgodnie z zasadą zachowania pędu możemy napisać:

Z zasady zachowania energii wyniknie natomiast, że:

Jeżeli te dwa równania połączymy w układ, a następnie rozwiążemy, po odpowiednim przekształceniu wyniku znajdziemy zmianę długości fali rozproszonego promieniowania:

Wielkość
(gdzie m₀ oznacza masę spoczynkową elektronu) występująca w powyższym wzorze jest stała i wynosi około 0,002426 nm. Nosi ona nazwę komptonowskiej długości fali.

Jak widać ze wzoru na zmianę długości fali, zmiana ta jest niezależna od długości początkowej, bardzo silnie zależy natomiast od kąta rozproszenia. Warto zauważyć, że dla α = 0˚, sin α = 0, a zatem zmiana długości fali nie następuje. W przypadku rozproszenia wstecznego (α = 180˚) zmiana długości jest największa.

Elektron, któremu foton przekazał część swojej energii, tzw. elektron komptonowski, jonizuje środowisko podobnie jak fotoelektron i podobnie jak on pod koniec ulega przyłączeniu do jakiegoś atomu lub jonu. Foton natomiast po zmianie długości fali i kierunku biegu porusza się dalej, zależnie od posiadanej energii bądź zapoczątkowując kolejne zjawiska Comptona, bądź ulegając absorpcji w zjawisku fotoelektrycznym.

ZJAWISKO TWORZENIA PAR ELEKTRON - POZYTON

Jeżeli energia fotonu jest większa od energii równoważnej masie spoczynkowej dwóch elektronów (czyli przewyższa 1,022 MeV), wzajemne oddziaływanie promieniowania i materii może mieć nieco inny przebieg. Przebiegając w pobliżu jądra, foton może w polu jego oddziaływania rozpaść się i wyzwolić dwie cząstki elementarne o przeciwnych ładunkach — elektron (negaton) i pozyton, sam ulegając unicestwieniu.

Elektron uzyskany podczas tego zjawiska jonizuje atomy kosztem swej energii kinetycznej. Pozyton natomiast, po utracie energii kinetycznej, jako cząstka nietrwała szybko łączy się (czyli ulega anihilacji) z jakimkolwiek napotkanym na swojej drodze elektronem. W tym procesie obie cząstki ulegają unicestwieniu, a na ich miejsce powstają dwa fotony, które następnie biorą udział w zjawisku fotoelektrycznym lub zjawisku Comptona.

PRAWO POCHŁANIANIA PROMIENIOWANIA

Jak każda fala, przechodząc przez warstwę materii zwaną absorbentem, promieniowanie elektromagnetyczne ulega pochłanianiu. Innymi słowy —natężenie wiązki tego promieniowania maleje. Zmiana natężenia zależy wykładniczo od grubości warstwy absorbentu, a opisana jest zależnością zwaną prawem pochłaniania promieniowania:

gdzie I₀ oznacza początkowe natężenie wiązki promieniowania,

d — grubość warstwy absorbentu,

I — natężenie promieniowania po przejściu przez tę warstwę,

e jest podstawą logarytmu naturalnego,

a μ — tak zwanym współczynnikiem ekstynkcji.

Często interesuje nas taka grubość warstwy, po przejściu przez którą natężenie promieniowania maleje do połowy. Wartość tę oznaczamy jako d_½ i nazywamy grubością warstwy połowiącej albo warstwą połówkowego osłabienia. Wiąże się ona ze współczynnikiem ekstynkcji zależnością:

Widzimy zatem, że jest ona odwrotnie proporcjonalna do wartości tego współczynnika.

WSPÓŁCZYNNIK EKSTYNKCJI

Współczynnik ekstynkcji jest wartością stałą dla każdego środowiska, przez które przebiega wiązka promieniowania. Jest on zasadniczo sumą trzech wielkości: współczynnika absorpcji τ, współczynnika rozpraszania σ i współczynnika π, związanego z utratą energii fotonów na powstawanie par elektron - pozyton.

W prawie pochłaniania promieniowania występuje współczynnik ekstynkcji tzw. liniowy, tzn. określający stopień osłabienia wiązki promieniowania w warstwie absorbentu o określonej grubości. Bardzo często zamiast niego stosujemy tzw. masowy współczynnik ekstynkcji, oznaczany jako μ_m.

Wprowadzenie takiej wielkości uniezależnia nas od gęstości absorbentu. Masowy współczynnik ekstynkcji określa nam stopień osłabienia wiązki promieniowania jako funkcję masy absorbentu przypadającej na 1 m² przekroju wiązki na przebytej przez nią drodze.

Masowy współczynnik ekstynkcji jest sumą masowych współczynników odpowiednio: absorpcji, rozpraszania i tworzenia par elektron - pozyton. Współczynniki te otrzymujemy, dzieląc wartości współczynników liniowych przez gęstość absorbentu.

Wielkość
, czyli masowy współczynnik absorpcji, okazuje się być powiązana zarówno z liczbą atomową Z absorbentu, jak i z długością fali absorbowanego promieniowania:

gdzie C' jest pewną stałą.

Wynika stąd, że pochłanianie promieniowania podczas przechodzenia przez materię zależy nie tylko od rodzaju i grubości warstwy tej materii, ale także od samego promieniowania. Analizując powyższą zależność, stwierdzamy bez trudu, że promieniowanie długofalowe, „miękkie” jest pochłaniane znacznie silniej niż „twarde”, bardziej przenikliwe promieniowanie o małej długości fali.

Oprócz współczynników liniowego i masowego wprowadzamy też trzecią wielkość, tzw. atomowy współczynnik ekstynkcji, oznaczany jako μ_at i dany wzorem:

gdzie A oznacza liczbę masową absorbentu,

a N jest liczbą Avogadra.

Atomowy współczynnik absorpcji τ_at, czyli
, również zależy od Z i λ, co podaje zależność:

gdzie c' jest nową stałą.

PÓŁPRZEWODNIKI

DEFINICJA I RODZAJE PÓŁPRZEWODNIKÓW

Półprzewodnikami nazywamy substancje, których opór właściwy w temperaturze pokojowej jest od 10³ do 10¹⁴ razy większy od oporu metali. Typowymi przedstawicielami półprzewodników są takie pierwiastki jak krzem, german, selen, a także różne siarczki i tlenki.

Właściwości przewodzące tych związków wyjaśnia mechanika kwantowa. Według niej elektrony w atomach wszystkich znanych pierwiastków znajdują się w określonych, przyporządkowanych sobie stanach energetycznych. Stany te łączą się w podpoziomy i poziomy energetyczne, wyróżniane w każdym osobnym atomie. Wiele ciał makroskopowych ma jednak strukturę krystaliczną. Wskutek silnych wzajemnych oddziaływań atomów w tej sieci poziomy energetyczne poszczególnych atomów rozpadają się na liczne podpoziomy, które leżą tak blisko siebie, że łączą się i zlewają ze sobą w ciągłe obszary, tak zwane pasma energetyczne. „Szerokość” energetyczna tych pasm, tzn. różnica energii między nimi, waha się w granicach od ułamków do ok. 10 eV. Między nimi znajdują się na ogół tzw. przerwy energetyczne — obszary, w których nie ma elektronów i poziomów energetycznych, mające podobną „szerokość” i noszące nazwę stref lub pasm wzbronionych.

Modele pasm energetycznych różnych ciała stałych przedstawia rysunek:

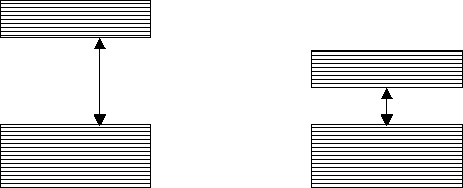
Rysunek A przedstawia izolator, rysunek B — metal.

Rysunek ten interpretujemy następująco: dolne pasmo energetyczne, zwane podstawowym lub walencyjnym, oddzielone jest od górnego, pasma przewodnictwa, strefą wzbronioną, która ma różną szerokość w zależności od rodzaju materiału. Pasmo podstawowe zapełniają elektrony nie poruszające się poza obrębem swojego atomu i nie biorące udziału w przenoszeniu ładunku. W paśmie przewodnictwa natomiast znajdują się elektrony, których swobodny ruch decyduje o przewodzeniu prądu przez dany materiał.

Okazuje się, że w metalach już w temperaturze zera bezwzględnego pasmo przewodnictwa jest częściowo zapełnione — dlatego też tak dobrze przewodzą one prąd. W izolatorach pasmo to jest puste, a ponadto strefa wzbroniona dzieląca je od pasma podstawowego jest tak „szeroka”, że do przejścia przez nią elektronowi trzeba byłoby dostarczyć ogromną ilość energii.

Z półprzewodnikami sprawa ma się nieco inaczej. W warunkach normalnych pasmo przewodnictwa jest w nich puste. Strefa wzbroniona między nim a pasmem walencyjnym nie jest jednak tak szeroka, jak w izolatorach, wobec czego elektrony mogą po dostarczeniu pewnej ilości energii przenosić się do niego — tym tłumaczy się zjawisko wzrostu przewodności półprzewodników ze wzrostem temperatury.

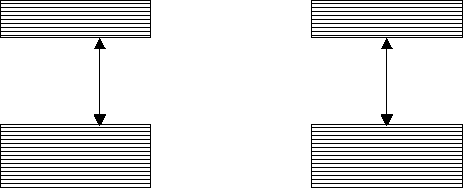
Rysunek A przedstawia półprzewodnik w temperaturze zera bezwzględnego. Zauważmy, że pasmo przewodnictwa jest puste (półprzewodnik zachowuje się jak izolator).

Rysunek B przedstawia półprzewodnik w temperaturze wyższej niż temperatura zera bezwzględnego. Jak widać, pod wpływem energii ruchów termicznych część elektronów przeniosła się z pasma podstawowego do pasma przewodnictwa. Puste miejsca pozostałe po nich w paśmie podstawowym nazywamy dziurami. Są one pod względem ładunku równoważne ładunkowi elektronu o znaku dodatnim. W polu zewnętrznym dziury te mogą zatem stać się nośnikiem ładunku ujemnego, a poruszają się w tym polu w kierunku przeciwnym niż elektrony.

Powyższa charakterystyka odnosi się do półprzewodników samoistnych, tzn. takich, które swoich właściwości przewodzących nie zawdzięczają żadnym domieszkom. Charakteryzują się one przewodnictwem mieszanym, elektronowo-dziurowym. W takich półprzewodnikach w każdej jednostce objętości znajduje się tyle samo nośników obydwu rodzajów (tj. elektronów i dziur).

Inaczej nieco jest w przypadku półprzewodników niesamoistnych, czyli tzw. domieszkowych. W takich półprzewodnikach liczby elektronów i dziur w jednostce objętości nie są sobie równe. Zależnie od rodzaju substancji dodanej do półprzewodnika samoistnego, na skutek procesów energetycznych, które nie zostaną tu opisane, w półprzewodniku tym pojawiają się dodatkowe elektrony lub dziury, mogące służyć jako nośniki ładunku.

Jeżeli domieszka powoduje powstanie przewagi dziur, w półprzewodniku zaczyna przeważać przewodnictwo dziurowe. Nazywamy go wówczas półprzewodnikiem typu p (positive). Jeżeli jest odwrotnie (przewaga elektronów nad dziurami), w przewodniku przeważa przewodnictwo elektronowe. Taki półprzewodnik nazywamy półprzewodnikiem typu n (negative).

DIODA PÓŁPRZEWODNIKOWA

Wyobraźmy sobie, że łączymy ze sobą dwa półprzewodniki: typu p i typu n.

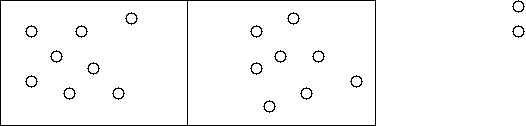
Elektrony i dziury dyfundują z półprzewodnika n do p i odwrotnie. Strumień elektronów dyfundujących z n do p jest jednak znacznie większy niż z p do n, tak samo jak strumień dziur dyfundujących z p do n jest większy niż z n do p. W wyniku tych procesów na złączu gromadzi się podwójna warstwa ładunków — ujemnego po stronie p, dodatniego po stronie n. W wyniku różnicy ładunków powstaje wówczas kontaktowa różnica potencjałów V_k, która hamuje dalszy przepływ. Ustala się stan równowagi dynamicznej.

Jeżeli teraz do układu półprzewodników przyłożymy napięcie zewnętrzne U_z, którego pole ma natężenie przeciwne do kierunku natężenia pola V_k, skok potencjału na złączu zmaleje. Stanie się tak, ponieważ pod wpływem pola zewnętrznego elektrony przewodnika n podążą ku złączu, i zrekombinują częściowo z nagromadzonymi tam dziurami, co spowoduje zmniejszenie ładunku dodatniego po tej stronie. Analogicznie stanie się w półprzewodniku typu p — znajdujące się w nim dziury podążą ku złączu, zmniejszając ładunek ujemny warstwy zaporowej. Zmniejszony skok potencjału na złączu spowoduje zmniejszenie oporu złącza w tym kierunku, co sprawia, że prąd jest przewodzony swobodnie. Kierunek ten nazywamy kierunkiem przewodzenia:

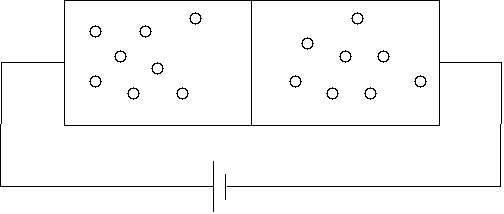
Jeżeli zmienimy kierunek napięcia zewnętrznego, zachodzące procesy będą odwrotne. Pod wpływem pola zewnętrznego elektrony w półprzewodniku n i dziury w półprzewodniku p zaczną podążać ku złączu, powodując zwiększanie grubości zaporowej warstwy ładunków. Skok potencjału na złączu rośnie, powodując wzrost oporu złącza w tym kierunku, co szybko uniemożliwia przepływ prądu. Kierunek ten nazywamy zaporowym:

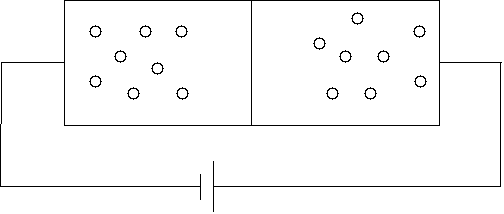
Złącze p-n będzie zatem przewodziło prąd lub hamowało go — w zależności od tego, w którą stronę będzie on płynął. Możemy powiedzieć, że działa ono jak prostownik, czyli przepuszcza prąd tylko w jednym kierunku przewodzenia. Z tego względu złącza p-n stosowane są często do prostowania prądów zmiennych. Są to tak zwane diody półprzewodnikowe.

CHARAKTERYSTYKA PRĄDOWO-NAPIĘCIOWA DIODY PÓŁPRZEWODNIKOWEJ

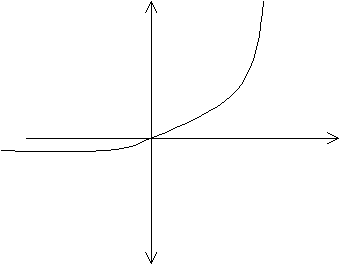
Zależność natężenia prądu przewodzenia i zaporowego (wstecznego) od wartości przyłożonego napięcia zewnętrznego U_z jest szczególną cechą złącza p-n, czyli diody półprzewodnikowej.

1. Natężenie prądu przewodzenia rośnie wykładniczo ze wzrostem napięcia U_z, osiągając wartości od kilku do kilkudziesięciu mA. Opór złącza (tzw. opór wewnętrzny diody) przez cały czas maleje;

2. Natężenie prądu wstecznego bardzo szybko (już przy kilku μA) osiąga stan nasycenia. Opór wewnętrzny diody wzrasta wraz ze wzrostem napięcia.

20218/L → 2374505

I

λ

A

B

C

D

I

I₁

I₂

I₃

λ

pasmo przewodnictwa

pasmo przewodnictwa

pasmo podstawowe

pasmo podstawowe

A

pasmo podstawowe

pasmo podstawowe

pasmo przewodnictwa

pasmo przewodnictwa

B

A

B

dziura

elektron

n

p

+

+

+

+

+

+

+

+

+

—

—

—

—

—

—

—

—

—

+

+

+

+

+

+

+

+

+

—

—

—

—

—

—

—

—

—

—

—

—

—

—

—

—

—

+

+

+

+

+

+

+

+

+

+

+

+

+

+

+

+

+

+

+

+

+

—

—

—

—

—

—

—

—

—

—

—

—

—

—

—

—

+

+

+

+

+

+

+

—

—

—

—

—

—

—

—

Wykres zależności natężeń prądu przewodzenia i wstecznego w zależności od wartości napięcia zewnętrznego.

I (mA)

I (μA)

U_z (V)

---