147

0x08 graphic
POLITECHNIKA Skład grupy: Rok studiów IV

WROCŁAWSKA Stajer Aldona Grupa II

Hałas Agnieszka Studia dzienne

Instytut Energoelektryki Bugajna Edyta Semestr VIII

WYDZIAŁ GÓRNICZY Klich Krzysztof Rok akademicki 1997/98

Laboratorium z Automatyki

Grupa Numer TEMAT: OCENA:

laboratoryjna ćwiczenia BADANIE TRANSFORMATORA

I JEDNOFAZOWEGO

Data wykonania 7

ćwiczenia

12.03.1998r.

CEL ĆWICZENIA:

Celem ćwiczenia było poznanie budowy i zasady działania transformatora oraz pomiarowe wyznaczenie jego podstawowych parametrów i charakterystyk.

SCHEMAT UKŁADU POMIAROWEGO DO BADANIA TRANSFORMATORA JEDNOFAZOWEGO

0x08 graphic

PROGRAM ĆWICZENIA I SPOSÓB JEGO WYKONANIA

1.Pomiar parametrów transformatora w stanie jałowym:

pomiar rezystancji uzwojeń transformatora za pomocą mostka Wheatson'a

R₁= 11 Ω - uzwojenie pierwotne;

przy zamkniętym wyłączniku W₁ i otwartym wyłączniku W₂ zwiększać za pomocą autotransformatora napięcie U₁ , aż do osiągnięcia wartości 1,1*Un;

Dokonano pomiarów prądu biegu jałowego I_o , napięcia U₂ i strat mocy w transformatorze dla różnych wartości napięcia U₁ . Wyniki pomiarów i obliczeń zestawiono w poniższej tabeli.

U₁	I₀	P₀	P_F_e	I_Fe	I_	Cosϕ_	U₂	K	R_Fe	X_
[V]	[A]	[W]	[W]	[A]	[A]	[-]	[V]	-	[Ω]	[Ω]
115	0,09	6	5,911	0,051	0,074	0,571	200	0,575	2237,39	1556,60
125	0,1	8	7,890	0,063	0,078	0,631	215	0,581	1980,35	1611,61
140	0,12	10	9,842	0,070	0,097	0,586	240	0,583	1991,55	1439,53
175	0,28	16	15,138	0,087	0,266	0,309	310	0,565	2023,11	657,14
185	0,4	18	16,240	0,088	0,390	0,219	325	0,569	2107,45	474,06
195	0,54	20	16,792	0,086	0,533	0,159	340	0,574	2264,42	365,79
205	0,72	24	18,298	0,089	0,714	0,124	360	0,569	2296,75	286,94
215	0,9	28	19,090	0,089	0,896	0,099	375	0,573	2421,42	240,06
225	1,05	32	19,873	0,088	1,046	0,084	390	0,577	2547,49	215,05
230	1,15	34	19,453	0,085	1,147	0,074	400	0,575	2719,44	200,54
240	1,4	40	18,440	0,077	1,398	0,055	420	0,571	3123,64	171,69

Podczas obliczeń korzystano z następujących wzorów:

czynna składowa prądu I₀;

straty mocy w rdzeniu;

rezystancja

reaktancja

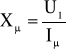
0x01 graphic

bierna składowa prądu I0;

przekładnia transformatora;

współczynnik przesunięcia kątowego;

WNIOSKI :

Podczas regulacji napięcia zasilającego U₁ zaobserwowano,że podczas jego zwiększania natężenie prądu przy biegu jałowym I_o transformatora rośnie liniowo a moc biegu jałowego P, też rośnie proporcjonalnie wraz ze wzrostem napięcia, straty mocy w rdzeniu transformatora ΔP_Fe również wzrastają natomiast współczynnik przesunięcia kątowego cos ϕ_o maleje.

Na podstawie otrzymanych wyników pomiarów sporządzono wykres wektorowy biegu jałowego transformatora i odpowiednie charakterystyki :

P_o =f(U₁) , I_o =f(U₁) , cos ϕ_o =f(U₁) .

Prąd I_ wymuszony napięciem U₁ i wytworzony strumień _f jest prądem indukcyjnym (_f i I_ są ze sobą w fazie).

Indukowana sem E₁₀ jest opóźniona w stosunku do _f o kąt 2 natomiast w stosunku do U₁ o kąt 

Prąd Fe ze wzrostem U1 zwiększa się liniowo natomiast prąd I wg charakterystyki magnesowania.

2.pomiar parametrów transformatora w czasie obciążenia:

przy wyłączonym obciążeniu zamknąć wyłączniki W₁ i W₂;

stopniowo zwiększać napięcie zasilające U₁ aż do osiągnięcia wartości

znamionowej ;

Wyniki otrzymanych pomiarów i obliczeń zestawiono w poniższej tabeli:

U₁	I₁	P₁	U₂	I₂	P₂	cos ϕ₁	cos ϕ₂	η
[V]	[A]	[W]	[V]	[A]	[W]	[-]	[-]	[-]
220	1.325	37.5	115	0.16	20	0.1286	1.0869	0.53
220	1.312	50	104	0.28	30	0.1732	1.0302	0.6
220	1.331	65	104	0.41	45	0.2219	1.0553	0.69
220	1.35	80	104	0.54	60	0.2693	1.0683	0.75
220	1.38	93.7	104	0.66	75	0.3086	1.0926	0.80
220	1.425	108.7	104	0.79	90	0.3467	1.0954	0.828

Obliczeń dokonano na podstawie następujących zależności:

współczynnik przesunięcia kątowego na uzwojeniu pierwotnym;

współczynnik przesunięcia kątowego na uzwojeniu wtórnym;

sprawność transformatora;

WNIOSKI :

Podczas zwiększania obciążenia transformatora, przy stałym napięciu zasilania zaobserwowano, że:

natężenie prądu na uzwojeniu pierwotnym I₁ wzrasta;
moc na uzwojeniu pierwotnym P₁ i wtórnym P₂wzrastają;
napięcie na uzwojeniu wtórnym U₂ jest stałe;
natężenie prądu na uzwojeniu wtórnym I₂ rośnie;
współczynnik przesunięcia kątowego na uzwojeniu pierwotnym

cos ϕ₁ rośnie;

na uzwojeniu wtórnym cos ϕ₂ również wzrasta o niewielką wartość;
sprawność transformatora wzrasta ;

Przy stałym napięciu wraz ze wzrostem natężenia na uzwojeniu pierwotnym następuje wzrost natężenia na uzwojeniu wtórnym. Pociąga to za sobą wzrost mocy czynnej oddawanej do odbiornika P₂ oraz mocy czynnej pobieranej z sieci P₁. Stosunek tych mocy do siebie również wzrasta co powoduje większą sprawność transformatora.

3.Pomiar parametrów transformatora w stanie zwarcia .

przy wyłączonym obciążeniu strony wtórnej zewrzeć przez amperomierz zaciski wtórne transformatora;

w obwodzie pierwotnym dopasować zakres pomiarowy woltomierza do pomiaru napięć o wartości do 30 V;

zwiększać powoli napięcie do wartości przy której prądy płynące w uzwojeniach osiągną wartości znamionowe;

Otrzymane wyniki i obliczenia zestawiono w poniższej tabeli:

U_z	I₁	I₂	K	P_z	cos ϕ_z	Z_z	R_z	X_z	e_z
[V]	[A]	[A]	[-]	[W]	[-]				[%]
3	5	2,10	1	10	0,53	0,6	0,4	0,45	90,9

Podczas obliczeń korzystano z poniższych wzorów:

0x01 graphic

. 100%

WNIOSKI:

Gdy wyłączniki W1 i W2 są zamknięte a wartość rezystancji obciążenia wynosi zero wówczas transformator znajduje się w stanie zwarcia. Fizycznie oznacza to, że oba końce uzwojenia wtórnego transformatora są ze sobą połączone metalicznie (przewodem). Stan zwarcia transformatora występuje wtedy , gdy napięcie wtórne U2=0 a uzwojenie pierwotne jest zasilane napięciem U1. Stan zwarcia jest najgrożniejszym stanem pracy transformatora. wpomiarowym stanie zwarcia napięcie pierwotne, przy którym płynące w obu uzwojeniach prądy osiągają swoje wartości znamionowe, nazywamy napięciem zwarcia.

Z_obc

I₂

W₂

U₂

U₁

W₁

I₁

Wyszukiwarka